转载

从原理推导逻辑斯蒂回归——Logit变换和潜在因子误差

逻辑斯蒂回归（Logistic Regression，以下简称LR）的应用还有工程学的思路一般介绍地都很清楚，大多数方法都从Sigmoid函数开始。本博文试图通过其他视角来重新理解LR是如何推导的。

Logit变换

对于预测一个分类变量，一个常见地推广OLS的方法就是直接采用

$$P(y = 1 | /theta, X) = /beta X$$

这个模型相当简单，我们用Andrew NG的图很容易就展现了这个OLS的推广模型的效果：

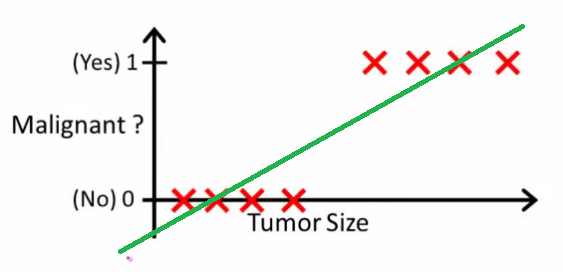
从原理推导逻辑斯蒂回归——Logit变换和潜在因子误差

但事实上，这个模型有一个致命的缺陷，即显然

$$/beta X /in (-/infty,+/infty)$$

显然这很违反逻辑。

从OLS到odds

一个显然的推广方案是，我们采用是概率比数方案即

$$odds(P) = /frac{P(y = 1 |/theta, X)}{P(y /neq 1 |/theta, X)} = /frac{P(y = 1 |/theta, X)}{1 - P(y = 1 |/theta, X)} = /beta X$$

这个好处是显然的，因为

$$odds(P) /in (0, + /infty)$$

但显然，我们还是没有 充分利用到 $/beta X$的值域。

从odds到LR

一个更简单地方案是讲odds对数化，这样的话，我们也将这个odds对数化的转化方式叫 logit 。

$$logit(p) = ln /frac{P(y = 1 |/theta, X)}{1 - P(y = 1 |/theta, X)} = /beta X$$

显然，

$$logit(p) /in (-/infty, +/infty)$$

我们真的充分利用到了线性模型的所有值了。

最后，我们可以得到

$${P(y = 1 |/theta, X)} = /frac {e^{/beta X}}{1 + e^{/beta X}}$$

此外，

$$logit^{-1}(x) = p = sigmoid(/beta X)$$

如何引入误差？—— 潜在因子解释LR

架设潜在因子

事实上，另一个对于LR的解释，就是来自于误差解释。在此，我们要构造一个潜在因子$Y^*$，满足以下条件

$$Y^* = /beta X + /epsilon$$

其中，

$$/epsilon /sim logistic(0, 1)$$

且，

$$Y = /begin{cases} 1, & Y^* > 0 // 0, & Y^* /le 0 /end{cases}$$

这样子，我们就引入了误差。

而同样地，我们来看这样如何可以推导出LR表达式。

首先，我们要知道，$$/int_{-/infty}^{x}logistic(x; 0, 1)dx = /frac{1}{1 + e ^ {- x}}$$的反函数为$logit(x)$，因此，我们可以做如下转换：

$$/begin{align}P(Y = 1| /theta, X) & = P(Y^* > 0) // & = P(/beta X + /epsilon > 0 ) // & = P(/epsilon > - /beta X) // & = P(/epsilon < /beta X) (因为logistic(0,1)是对称的)// & = logit^{-1}(/beta X)（用反函数原理）// & = p/end{align}$$

因此，可以看到logit变换解释和潜在因子解释是等价的，因此潜在因子模型可以直接推导出LR。

Rasch模型

心理学家Rasch ¹ 在1960年的书中想要研究一个简单的学生能力、题目难度和题目是否答出（二选项）的关系。

他提出了一个很好的解决方案。首先他把衡量学生能力的值转化成一个权重，于此同时对某个问题的难度也做如是处理。其次，他建立了一个度量（measurement），简单地表述为：

$$measurement = weight_{学生能力} - weight_{题目难度}$$

然后找到一条界限，来判断学生是否答对。

显然，这个模型和之前所说的潜在因子模型形式上是一致的，但值得注意的是，这里的度量不带有任何统计学意义，他不和之前的$Y^*$完全一致。简单地说，度量简简单单是一个学生回答问题的度量，而不是学生答对问题的概率。

logit变换试图说明学生在总体上的表现，而某个学生只是这个总体的一个样本；而Rasch模型试图解释的是一个个体水平上正确完成某个问题的能力，而不是回答某个问题的概率；
logit变换解释采用的是分布的、统计的解释；而Rasch模型则是来源于物理上的度量概念；
显然，这个模型中的学生能力和题目难度完全可以量化成有意义可度量的指标；而logit模型更倾向于描述成一个概率问题，和某个学生个体无关。
在Rasch的例子中，我们并不需要把结果还原成复杂的logistic函数，相反，度量就简洁地直接表达了模型本身。

所以，我们要理解，潜在因子解释（Rasch模型解释）和Logit变换解释在本质上是物理学和统计学理解世界的差异，是对个体特征的量化和对分布预测的差异。

此外，Rasch例子想表达的另一个含义是， LR模型是没有误差 的，因为标准LR模型是基于Logit变换的而不含有潜在因子假说的，在计算每个样本$Y - /hat{Y}$时，显然，是对个体已经完成二项选择后的描述，此时，用总体分布的概率描述这个现象是有的问题的（但残差定义依旧存在）。因此，大多数书中会避免以下写法：

$$logit(p) = /beta X + /epsilon$$

如果要引入误差的概念，必须要用到Rasch模型中同构的潜在因子解释。

原文 https://segmentfault.com/a/1190000008046030

正文到此结束