Logistic 函数 vs Softmax 函数
嘿，大家好。你知道机器学习中的分类模型么？你知道 Softmax 和 Logistic 函数么？如果你不是很了解这些内容的话，那么请继续往下看吧。
众所周知，机器学习中最经典的模型是分类模型。根据维基百科的叙述，分类模型（监督学习模型）是根据标记数据来推断未知样本归属类别的模型。
为了简化起见，我们的数据集中标签的数目必须是有限的，即对于一张猫的照片我们需要计算机告诉我们这是一只猫。
本文中用到的图片全部来自于 Pixabay ( https://pixabay.com/)，该网站上提供了许多免费照片。
首先我们来看一个简单的分类模型——二分类问题，比如判断图片中是否存在猫。本文中主要采用一个黑箱模型——神经网络模型，不过本文的重点并不是介绍神经网络模型的建模过程，而是关注该模型的最后一个计算步骤。
对于黑箱模型来说，我们无法得知其内部的构建过程，我们只能得到给定输入结果对应的预测标签。相反地，同样存在白箱模型，我们不但能获取输出结果，还能得知模型的内部结构。
因此，神经网络的计算模块是一个黑箱过程，我们输入一张图片，该模型返回相应的标签结果。输出结果如下所示：
为了获得输出结果所对应的标签情况，我们需要利用 logistic 函数，其形式如下所示：
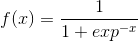
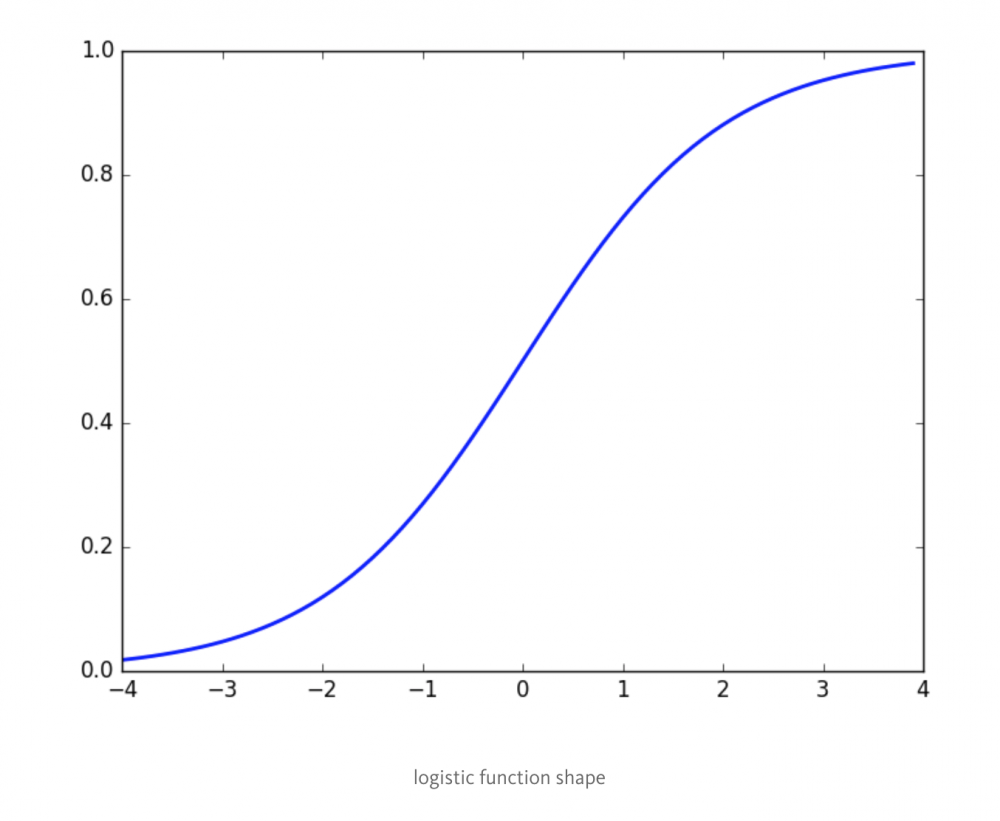
从上图我们可以看出，该函数可以很好地处理二分类问题：当概率值大于 0.5 时，我们认为该样本属于类 ‘1’，而当概率值小于 0.5 时，我们认为该样本属于类 ‘0’。
转换后的结果如下所示：
那么，什么是 Softmax 函数呢？该函数通常用于处理多分类问题，它可以计算得到样本归属于每个类别的概率。
比如，
那么问题来了，给定某个样本它归属于每个类别的概率分别是多少呢？我们假设每个样本只能有一个标签，此时我们利用 Softmax 函数即可获得样本归属于每个类别的概率，该函数的形式非常简单：
因此，我们可以得到给定样本的概率向量：
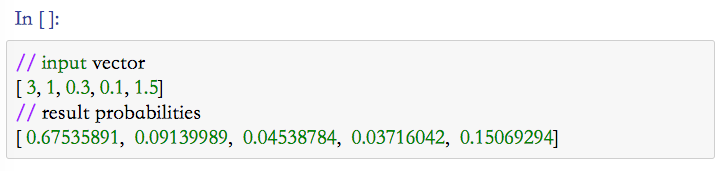
需要注意的是，这些概率值的总和为1。
总结
- Softmax 函数通过给定的任意向量输出对应的概率值，它可以处理多标签分类问题。
Logistic 函数通过给定的任意向量输出 Sigmoid 函数的值，它可以处理二分类问题。
如果你发现本文中存在问题，请及时告诉我，我很乐意听到这些消息并从中学会更多的知识。
一些有用的链接
- Udacity course on ML
- Wikipedia article for sigmoid function
- Wikipedia article for softmax function
原文链接： https://medium.com/@demidovs/ml-1-logistic-function-vs-softmax-44c73399c3c4#.78vsb0ato
原文作者：Alexander Demidovskij
译者：Fibears
正文到此结束
热门推荐
相关文章
近期评论
-
666
-
文章和留言都翻到11页了 没有OOM
-
-
朋友，翻页到11页，及以后，会出现OOM，无法访问
-
-
-
-
版本号是多少，你可以下载哪个代码仓库，jdk选1.8 直接跑就行
-
-
Loading...
![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)
