转载

最短路径-Dijkstra

在日常生活中，我们如果需要常常往返A地区和B地区之间，我们最希望知道的可能是从A地区到B地区间的众多路径中，那一条路径的路途最短。最短路径问题是图论研究中的一个经典算法问题，旨在寻找图（由结点和路径组成的）中两结点之间的最短路径。

用于解决最短路径问题的算法被称做“最短路径算法”，有时被简称作“路径算法”。最常用的路径算法有：Dijkstra算法、A*算法、Bellman-Ford算法、Floyd-Warshall算法、Johnson算法。

Dijkstra算法是典型最短路算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。Dijkstra算法能得出最短路径的最优解。本篇博客将详细介绍狄克斯特拉(Dijkstra算法)

Dijkstra算法思想

Dijkstra算法思想为：设G=(V,E)是一个带权有向图，把图中顶点集合V分成两组，第一组为已求出最短路径的顶点集合（用S表示，初始时S中只有一个源点，以后每求得一条最短路径 , 就将加入到集合S中，直到全部顶点都加入到S中，算法就结束了），第二组为其余未确定最短路径的顶点集合（用 U表示），按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中，总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外，每个顶点对应一个距离，S中的顶点的距离就是从v到此顶点的最短路径长度，U中的顶点的距离，是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。

这些叙述性的思想看的人头晕，下面用例子来一步步讲解。

我们要使用到的图如下：

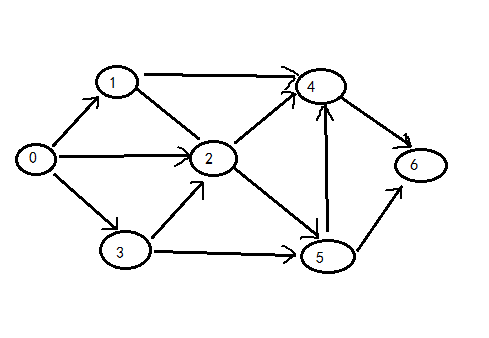
最短路径-Dijkstra

我们使用二维数组对其数据化：

#define INF 10000 //表示不可到达  #define MAXSIZE 7 //表示图的结点数  //邻接矩阵存储图的信息 int map[MAXSIZE][MAXSIZE]={  {0,4,6,6,INF,INF,INF},  {INF,0,1,INF,7,INF,INF},  {INF,INF,0,INF,6,4,INF},  {INF,INF,2,0,INF,5,INF},  {INF,INF,INF,INF,0,INF,6},  {INF,INF,INF,INF,1,0,8},  {INF,INF,INF,INF,INF,INF,0} };

定义多个数组来记录：

away[i]: 起点到顶点i的目前最短路径长度

path[]:保存最短路径

s[]: 标记是否已找到最短路径，1表示已找到

画出Dijkstra算法步骤图如下：

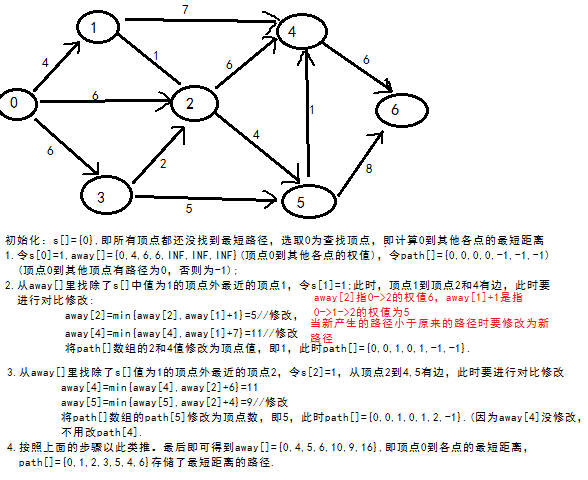最短路径-Dijkstra 理解了Dijkstra算法的步骤后，写出其代码为：

void Dijkstra(int v) {  int away[MAXSIZE];//保存到各个点的最短距离  int path[MAXSIZE];//最短距离路径  int already[MAXSIZE]={0};//是否已经找到最短距离，1表示找到了，对应上图的s[]   for(int i=0;i<MAXSIZE;i++)  {   away[i]=map[v][i];//获取权值    if(away[i]<INF)//存在路径为0    path[i]=0;   else    path[i]=-1;//不存在路径为-1   }  already[v]=1;//把顶点v加入到找到数组里   //开始寻找最短距离  int min,ok;  for(int i=0;i<MAXSIZE;i++)  {      min=INF;   for(int k=0;k<MAXSIZE;k++)   {    if(already[k]==0&&away[k]<min)//找away里的最小值，且该顶点不在already里    {     min=away[k];     ok=k;//记录最小的顶点    }   }   already[ok]=1;//把顶点ok加入到找到数组里    //修改away和path数组   for(int j=0;j<MAXSIZE;j++)   {    if(already[j]==0)//此结点还没有最短距离    {     if(map[ok][j]<INF&&(away[ok]+map[ok][j])<away[j])     {      away[j]=away[ok]+map[ok][j];      path[j]=ok;//修改path,修改过away权值的把path改为顶点值     }    }   }      }    }

得到path[]数组后，我们还要根据path的值来计算顶点0到各点的路径。

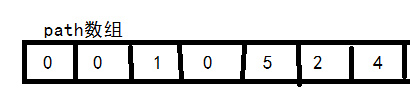
最短路径-Dijkstra

如我们要求顶点0到顶点6的路径：

步骤如下：

path[6]=4;

path[4]=5;

path[5]=2;

path[2]=1;

path[1]=0;(一旦值为0，则结束，且这个0不能算进去）

加上 起点0（不是最后算出来那个0） 和终点6，则其路径为0->1->2->5->4->6（倒叙）,

最短路径为away[6]=16

计算路径的代码为：

for(int s=0;s<MAXSIZE;s++)  {   if(s!=v)//除去起点   {    if(already[s]==1)    {     cout<<endl<<"从顶点"<<v<<"到顶点"<<s<<"的最小距离为： "<<away[s]<<"  "<<"路径为: ";          vector<int>temp;     temp.insert(temp.begin(),s);//把终点插入     int ok=s;     while(true)     {        ok=path[ok];        if(ok==0)//停止         break;        temp.insert(temp.begin(),ok);//把起点插入            }     temp.insert(temp.begin(),v);//把起点插入     for(int z=0;z<temp.size();z++)      cout<<temp[z]<<" ";    }    else     cout<<endl<<"从顶点"<<v<<"到顶点"<<s<<"不存在路径"<<endl;   }  }

至此，就完成了Dijkstra算法求最短路径的问题，主要是要理解Dijkstra算法的过程，特别是away[]和path[]

两个数组的变化。

正文到此结束