转载

算法复杂度和大O表示法

概念

算法复杂度和大O表示法算法复杂度是算法分析里的概念（对应到 SICP 里的增长阶），是衡量计算资源消耗数量（例如计算时间，存储器使用等）的指标。

算法的复杂度在理论上表示为一个函数：其定义域是输入数据的长度（通常考虑任意大的输入，没有上界），值域通常是执行步骤数量（时间复杂度）或者存储器位置数量（空间复杂度）。

这个函数形如：

R(n) = Θ(f(n)) 亦可记做 O(f(n))

f(n) 就是被度量的算法主体；算法的复杂度标记就是大O（Θ读做theta），这种记法称为大O表示法。

常见复杂度级别

Θ(1) 常数级别
Θ(log(n)) 对数级别
Θ(n) 线性级别
Θ(n*log(n)) 线性对数级别
Θ(n^2) 平方级别
Θ(2^n) 指数级别
…

直观感受

规模n 与复杂度的关系：

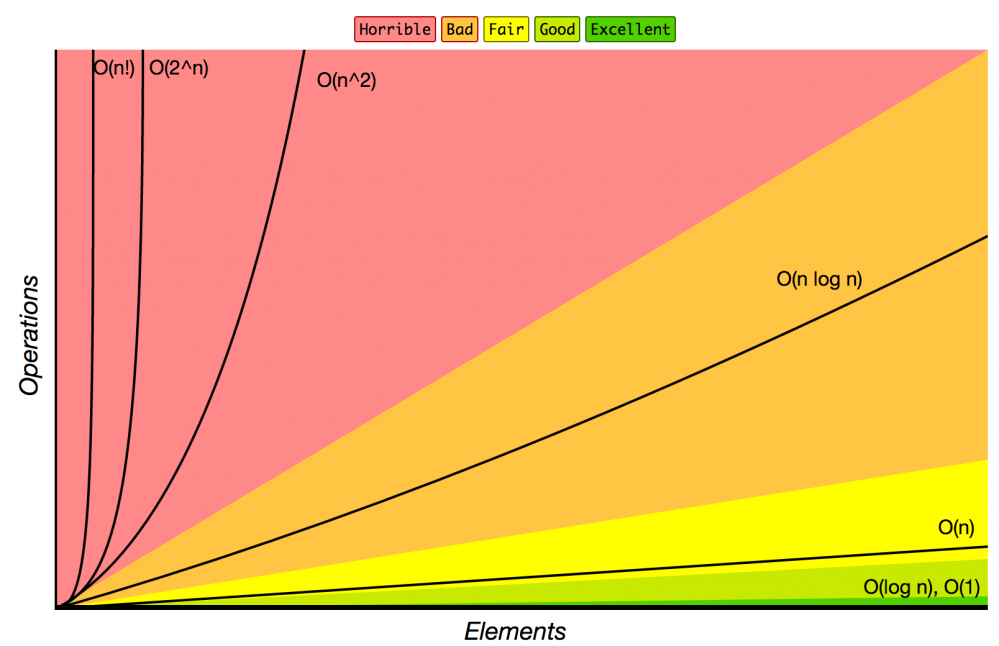
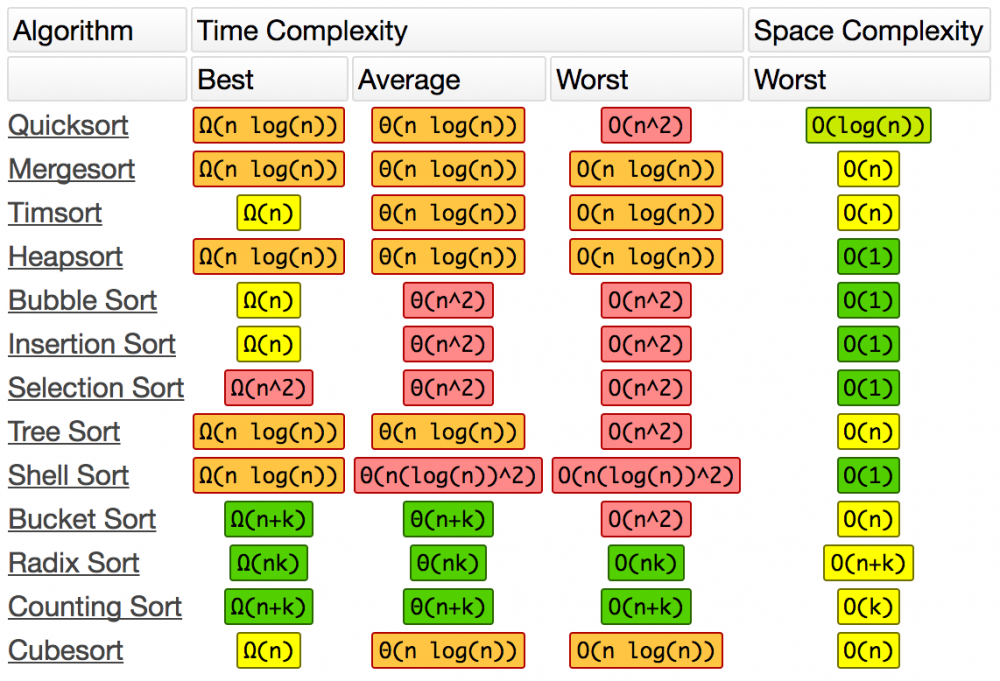
算法复杂度和大O表示法

各种排序算法的复杂度：

算法复杂度和大O表示法

例子

求幂算法 b^n（b的n次方），如果使用递归的形式来表达，有：

b^n = b * b^(n-1)
b^0 = 1

我们用 Racket 将它翻译为如下过程：

; 线性递归算幂
(define (expt b n)
    (if (= n 0)
        1
        (* b (expt b (- n 1)))))

可以看出，对于任意的输入规模 n，它都是线性的递归计算（ 线性递归 ），时间和空间复杂皆为 Θ(n) 。

我们知道，有限递归算法都可以优化成 线性迭代 形式，于是就有了：

; 线性迭代算幂
(define (linear-exp m n)
  (define (linear-exp-iter m n acc)
    (cond ((= n 0) 1)
          ((= n 1) (* acc m))
          (else (linear-exp-iter m (- n 1) (* acc m)))
          ))
  (linear-exp-iter m n 1)
)

不难发现，这个算法的时间复杂度还是线性的，变换成迭代形式后，优化的是空间复杂度，降至了 Θ(1) 。

还有优化的余地，因为，幂函数可以表示为：

b^n = (b^(n/2))^2 当n是偶数时

b^n = b * b^(n-1) 当n是奇数时

所以，算法可以通过迅速降幂，优化成 对数级别 ：

; 对数递归算幂
(define (fast-expt b n)
  (define (square x) (* x x))
  (cond ((= n 0) 1)
        ((even? n) (square (fast-expt  b (/ n 2))))
        (else (* b (fast-expt b (- n 1))))))

时间和空间上复杂度皆为 Θ(log(n)) 。

所以，递归就一定比迭代算法慢吗？未必~