转载

BigDecimal学习笔记之Double转BigDecimal

Java中BigDecimal类有这么一个方法：

public BigDecimal(double val);

它是将一个double类型的数据转换成BigDecimal。double内部使用64bit来表示一个数，这样空间效率极高，但牺牲了精度；而BigDecimal内部使用BigInteger来存储有效数，不存在精度丢失的情况但空间效率较差。double和BigDecimal都有其使用的场景，没有绝对好坏。

下面是这个方法的内部实现源码：

public BigDecimal(double val, MathContext mc) {
    if (Double.isInfinite(val) || Double.isNaN(val))
        throw new NumberFormatException("Infinite or NaN");
    // Translate the double into sign, exponent and significand, according
    // to the formulae in JLS, Section 20.10.22.
    long valBits = Double.doubleToLongBits(val);
    int sign = ((valBits >> 63) == 0 ? 1 : -1);
    int exponent = (int) ((valBits >> 52) & 0x7ffL);
    long significand = (exponent == 0
            ? (valBits & ((1L << 52) - 1)) << 1
            : (valBits & ((1L << 52) - 1)) | (1L << 52));
    exponent -= 1075;
    // At this point, val == sign * significand * 2**exponent.

    /*
     * Special case zero to supress nonterminating normalization and bogus
     * scale calculation.
     */
    if (significand == 0) {
        this.intVal = BigInteger.ZERO;
        this.scale = 0;
        this.intCompact = 0;
        this.precision = 1;
        return;
    }
    // Normalize
    while ((significand & 1) == 0) { // i.e., significand is even
        significand >>= 1;
        exponent++;
    }
    int scale = 0;
    // Calculate intVal and scale
    BigInteger intVal;
    long compactVal = sign * significand;
    if (exponent == 0) {
        intVal = (compactVal == INFLATED) ? INFLATED_BIGINT : null;
    } else {
        if (exponent < 0) {
            intVal = BigInteger.valueOf(5).pow(-exponent).multiply(compactVal);
            scale = -exponent;
        } else { //  (exponent > 0)
            intVal = BigInteger.valueOf(2).pow(exponent).multiply(compactVal);
        }
        compactVal = compactValFor(intVal);
    }
    int prec = 0;
    int mcp = mc.precision;
    if (mcp > 0) { // do rounding
        int mode = mc.roundingMode.oldMode;
        int drop;
        if (compactVal == INFLATED) {
            prec = bigDigitLength(intVal);
            drop = prec - mcp;
            while (drop > 0) {
                scale = checkScaleNonZero((long) scale - drop);
                intVal = divideAndRoundByTenPow(intVal, drop, mode);
                compactVal = compactValFor(intVal);
                if (compactVal != INFLATED) {
                    break;
                }
                prec = bigDigitLength(intVal);
                drop = prec - mcp;
            }
        }
        if (compactVal != INFLATED) {
            prec = longDigitLength(compactVal);
            drop = prec - mcp;
            while (drop > 0) {
                scale = checkScaleNonZero((long) scale - drop);
                compactVal = divideAndRound(compactVal, LONG_TEN_POWERS_TABLE[drop], mc.roundingMode.oldMode);
                prec = longDigitLength(compactVal);
                drop = prec - mcp;
            }
            intVal = null;
        }
    }
    this.intVal = intVal;
    this.intCompact = compactVal;
    this.scale = scale;
    this.precision = prec;
}

代码不长，但理解起来需要一点背景知识。我们来逐行分析。

long valBits = Double.doubleToLongBits(val);

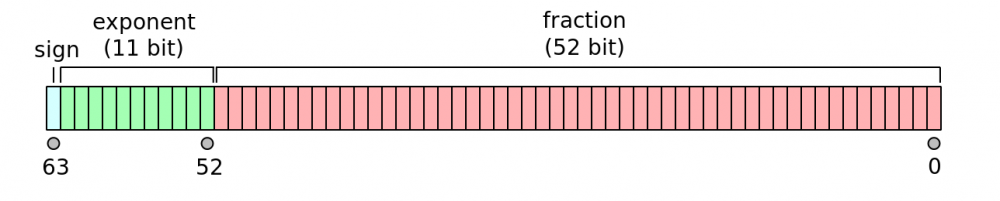
这一步是获取double的内部表示，一共64bit，刚好为long的长度。valBits采用BigEnding（大端序）表示，包含1个符号位，11个指数位，52个有效数位。格式如下所示：

BigDecimal学习笔记之Double转BigDecimal

int sign = ((valBits >> 63) == 0 ? 1 : -1);
int exponent = (int) ((valBits >> 52) & 0x7ffL);
long significand = (exponent == 0
        ? (valBits & ((1L << 52) - 1)) << 1
        : (valBits & ((1L << 52) - 1)) | (1L << 52));
exponent -= 1075;

这几步是解析64bit的double数据，将其分成三部分：sign（符号），exponent（指数）和significand（有效数）。上面四条语句执行完后，double所代表的数值等于（sign * significand * 2 ^exponent ）。第一和第二行代码根据位置直接获取sign和exponent，但是第三和第四条语句对significand和exponent做了一些处理，这里我们主要理解后两条语句。

double内部使用科学技术法来表示数据，如下所示：

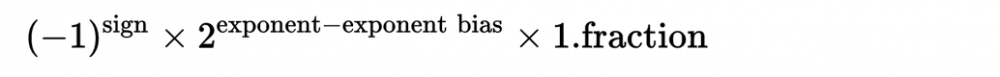
BigDecimal学习笔记之Double转BigDecimal

sign为符号位，exponent为指数。exponent bias为指数偏移值（1023），这个是什么东西？double的指数位exponent有11位，这11位表示了一个无符号整数。实际的指数值需要将其减去指数偏移值（1023）得到。

举个例子，假如这11位十六进制为#400，即十进制的1024。那么这个double的指数实际为1024 - 1023 = 1。

那1.fraction又是怎么来的呢？其实1.fraction是由double的52位有效数得来的。对于一个只包含0和1的二进制数，我们总可以通过科学计数法将其化成1.xxx格式的有效数（当然0除外），因此为了增加表示double的表示范围，我们可以省略最高位1的存储，只存储小数部分，也就是52位的有效数。

而指数部分为最小值#000时，double的科学技术表示为如下所示：

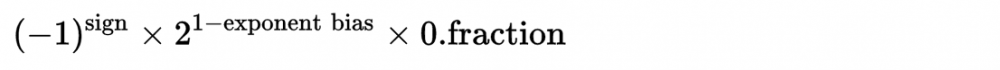
BigDecimal学习笔记之Double转BigDecimal

上面的1.fraction变成了0.fraction。虽然直观上觉得这种特殊情况处理不太优美，但想想也在情理之中，要不然数字0怎么用double表示呢？

背景知识已说完，我们来看下上面的第三条语句：

long significand = (exponent == 0
        ? (valBits & ((1L << 52) - 1)) << 1
        : (valBits & ((1L << 52) - 1)) | (1L << 52));

这条语句表达的意思就是：当指数部分为0时，以0.fraction方式取出有效数；当指数部分不为0时，以1.fraction方式取出有效数。此外，我们希望significand保存的是一个整数，我们只需在科学计数法中将指数部分再减去52，significand存储的数据就可以看做是整数了。

这也就是第四行代码表达的意思：

exponent -= 1075;

1075 = 1023 + 52，也就是指数部分减去指数偏移值和用于化整的52。

至此，代码最难理解（个人认为）的一部分已经解构完毕。这几行代码使用了sign、exponent和significand来表示double所代表的数据，即：

double的数据 = sign * significand * 2 ^exponent

下面我们接着分析代码。

if (significand == 0) {
    this.intVal = BigInteger.ZERO;
    this.scale = 0;
    this.intCompact = 0;
    this.precision = 1;
    return;
}

当有效数为0的时做特殊处理。

这里说下BigDecimal的内部表示。它主要由intVal、scale、intCompact、precision表示：

intVal类型为BigInteger，用大整数来表示有效数。
precision表示精度，也就是有效数有多少位。
scale表示范围，也就是小数部分占多少位。
intCompact类型为long，当有效数的绝对值不超过Long.MAX_VALUE时，使用intCompact来存储有效数提高计算效率。

while ((significand & 1) == 0) { // i.e., significand is even
    significand >>= 1;
    exponent++;
}

这是通过将有效数右移方式（也就是除以2）化成奇数形式。

int scale = 0;
// Calculate intVal and scale
BigInteger intVal;
long compactVal = sign * significand;
if (exponent == 0) {
    intVal = (compactVal == INFLATED) ? INFLATED_BIGINT : null;
} else {
    if (exponent < 0) {
        intVal = BigInteger.valueOf(5).pow(-exponent).multiply(compactVal);
        scale = -exponent;
    } else { //  (exponent > 0)
        intVal = BigInteger.valueOf(2).pow(exponent).multiply(compactVal);
    }
    compactVal = compactValFor(intVal);
}

这里是将上面的（sign * significand * 2 ^exponent ）转换成intVal、compactVal和scale。

可以看到，判断条件对于指数的值分了三种情况，等于0，小于0和大于0。

exponent等于0时，判断了compactVal（即sign * significand）的值是否等于INFLATED（即Long.MIN_VALUE）。但其实这个判断永远为false，因为根据之前的计算此处significand不会超过53位数，因此sign * significand无论如何也不可能等于Long.MIN_VALUE。
exponent小于0时，sign * significand * 2 ^exponent 表示一个小数，代码采取了有效数化整、增加小数位的方法，将有效数设为5 ^-exponent * sign * significand，小数位增加（-exponent）位。这是为什么呢？计算过程如下（数学渣，求轻拍）：

BigDecimal学习笔记之Double转BigDecimal

exponent大于0时，sign * significand * 2 ^exponent 表示整数，直接计算即可。

接着分析剩下代码。

int prec = 0;
int mcp = mc.precision;
if (mcp > 0) { // do rounding
    int mode = mc.roundingMode.oldMode;
    int drop;
    if (compactVal == INFLATED) {
        prec = bigDigitLength(intVal);
        drop = prec - mcp;
        while (drop > 0) {
            scale = checkScaleNonZero((long) scale - drop);
            intVal = divideAndRoundByTenPow(intVal, drop, mode);
            compactVal = compactValFor(intVal);
            if (compactVal != INFLATED) {
                break;
            }
            prec = bigDigitLength(intVal);
            drop = prec - mcp;
        }
    }
    if (compactVal != INFLATED) {
        prec = longDigitLength(compactVal);
        drop = prec - mcp;
        while (drop > 0) {
            scale = checkScaleNonZero((long) scale - drop);
            compactVal = divideAndRound(compactVal, LONG_TEN_POWERS_TABLE[drop], mc.roundingMode.oldMode);
            prec = longDigitLength(compactVal);
            drop = prec - mcp;
        }
        intVal = null;
    }
}

这里主要根据MathContext设置的精度限制来取精抛弃多余位数。当mc.precision设置特定值（大于0）时，需要取精。

在取精计算中，主要分为两部分计算，即if (compactVal == INFLATED)和if (compactVal != INFLATED)两个分支。

第一个分支if (compactVal == INFLATED)表达的意思为，如果BigDecimal的有效数很大，而且精度也超出设置的特定值，那么对intVal取精，直到 符合精度要求 或者 用一个long足以表示 。

第二个分支if (compactVal != INFLATED)表达的意思为，如果BigDecimal的有效数足够用compactVal表示，那么对compactVal进行取精，将原有效数字段intVal字段设为null回收空间。

至此，代码分析完毕。

参考资料：