机器学习的数学基础：矩阵篇

前言

机器学习如火如荼，要学习机器学习，数学基础少不了。所以本系列将对机器学习所用到的线性代数、微积分和概率统计的基础知识做一个简单的概括。

本文将总结线性代数中矩阵的基本知识点。同时理论结合实践，使用 Python 来进行实践。如果需要跟着进行编程实践，请先确保下列环境已安装：

• Python - 编程实践所使用的语言；
• Numpy - Python 的数值计算库。

矩阵（Matrix）是人为约定的一种数据的表示方法，在图像处理、人工智能等领域，使用矩阵来表示和处理数据非常常见。一个矩阵的举例：

/[/mathbf{A}_{2 /times 3}=/begin{bmatrix} 5 & 2 & 7 // 1 & 3 & 4 /end{bmatrix}/]

其中，矩阵 /(/mathbf{A}/) 的下标 /(2 /times 3/) 表示 /(/mathbf{A}/) 是一个 2 行 3 列的矩阵。类似的，另一个示例：

/[/mathbf{ B }_{ 4 /times 4 }=/begin{bmatrix} 5 & 2 & 7 & 6 // 1 & 3 & 4 & 2 // 7 & -1 & 9 & 0 // 8 & 2 & -2 & 3 /end{bmatrix}/]

再看回矩阵 /(/mathbf{A}/) ，如果要表示第 2 行的第 2 个元素 3 ，可以使用 /(/mathbf{A}[2, 2]/) 或 /(a_{2,2}/)。

使用 Python 创建矩阵很简单：

import numpy as np
a = np.matrix('5 2 7;1 3 4')
b = np.matrix('5 2 7 6;1 3 4 2;8 2 -2 3')

也可以用下面这种形式：

import numpy as np
a = np.matrix([[5,2,7],[1,3,4]])
b = np.matrix([[5,2,7,6],[1,3,4,2],[8,2,-2,3]])

两种形式完全等效。但第一种更简明直观，不容易犯错。因此推荐第一种方式。

要取出矩阵中的某个值，可以使用类似数组的下标运算符。但要注意的是，计算机是以 0 开始计数的。例如，要取出 /(/mathbf{A}[2,2]/) ，应该使用：

>>> a[1,1]
a[1,1]
3

基本运算

加

矩阵加法的定义非常符合直觉。假设有 /(/mathbf{ A }_{ 3 /times 3 }=/begin{bmatrix} 1 & 0 & 1 // 1 & 2 & 1 // 2 & 1 & 1 /end{bmatrix}/) ， /(/mathbf{ B }_{ 3 /times 3 }=/begin{bmatrix} 2 & 1 & -1 // 0 & -1 & 2 // 2 & -1 & 0 /end{bmatrix}/) ，则:

/[/mathbf{A}+/mathbf{B} = /begin{bmatrix} 1 & 0 & 1 // 1 & 2 & 1 // 2 & 1 & 1 /end{bmatrix} + /begin{bmatrix} 2 & 1 & -1 // 0 & -1 & 2 // 2 & -1 & 0 /end{bmatrix} = /begin{bmatrix} 1+2 & 0+1 & 1+(-1) // 1+ 0 & 2+(-1) & 1+2 // 2+2 & 1+(-1) & 1+0 /end{bmatrix} = /begin{bmatrix} 3 & 1 & 0 // 1 & 1 & 3 // 4 & 0 & 1 /end{bmatrix} /]

要注意两个矩阵的行数和列数必须相同，否则无定义。

Python 示例：

>>> a = np.matrix('1 0 1;1 2 1;2 1 1')
a = np.matrix('1 0 1;1 2 1;2 1 1')
>>> b = np.matrix('2 1 -1;0 -1 2;2 -1 0')
b = np.matrix('2 1 -1;0 -1 2;2 -1 0')
>>> a + b
a + b
matrix([[3, 1, 0],
        [1, 1, 3],
        [4, 0, 1]])

很容易看出，矩阵的加法满足交换律和结合律，即 /(/mathbf{A} + /mathbf{B} = /mathbf{B} + /mathbf{A}/)， /((/mathbf{A} + /mathbf{B}) + /mathbf{C} = /mathbf{A} + (/mathbf{B} + /mathbf{C})/)。

减

矩阵减法也和加法一样简单。对于上面给出的 /(/mathbf{A}/) 和 /(/mathbf{B}/)，有：

/[/mathbf{A}-/mathbf{B}=/begin{bmatrix} 1 & 0 & 1 // 1 & 2 & 1 // 2 & 1 & 1 /end{bmatrix}-/begin{bmatrix} 2 & 1 & -1 // 0 & -1 & 2 // 2 & -1 & 0 /end{bmatrix}=/begin{bmatrix} 1-2 & 0-1 & 1-(-1) // 1-0 & 2-(-1) & 1-2 // 2-2 & 1-(-1) & 1-0 /end{bmatrix}=/begin{bmatrix} -1 & -1 & 2 // 1 & 3 & -1 // 0 & 2 & 1 /end{bmatrix}/]

同样，相减的两个矩阵行数和列数必须完全相同，否则无定义。

Python 示例：

>>> a - b
a - b
matrix([[-1, -1,  2],
        [ 1,  3, -1],
        [ 0,  2,  1]])

乘

矩阵乘法的定义是 /(/mathbf{A}_{i /times j}/) 矩阵的每一行的元素分别与 $/mathbf{B}_{j /times k} $ 矩阵的每一列的元素两两相乘并相加，从而得到一个新的矩阵 /(/mathbf{C}_{i /times k}/) 。两个矩阵能相乘的充分必要条件是第一个矩阵的列数与第二个矩阵的行数相等，否则无定义。例如，对于上面给出的 /(/mathbf{A}/) 和 /(/mathbf{B}/)，有：

/[/begin {aligned} /mathbf{A} /times /mathbf{B} &=/begin{bmatrix} 1 & 0 & 1 // 1 & 2 & 1 // 2 & 1 & 1 /end{bmatrix}/times /begin{bmatrix} 2 & 1 & -1 // 0 & -1 & 2 // 2 & -1 & 0 /end{bmatrix} /// &=/begin{bmatrix} 1/cdot 2+0/cdot 0+1/cdot 2 & 1/cdot 1+0/cdot (-1)+1/cdot (-1) & 1/cdot (-1)+0/cdot 2+1/cdot 0 // 1/cdot 2+2/cdot 0+1/cdot 2 & 1/cdot 1+2/cdot (-1)+1/cdot (-1) & 1/cdot (-1)+2/cdot 2+1/cdot 0 // 2/cdot 2+1/cdot 0+1/cdot 2 & 2/cdot 1+1/cdot (-1)+1/cdot (-1) & 2/cdot (-1)+1/cdot 2+1/cdot 0 /end{bmatrix}/// &=/begin{bmatrix} 4 & 0 & -1 // 4 & -2 & 3 // 6 & 0 & 0 /end{bmatrix} /end {aligned} /]

再举一个行列数不同的例子， 假设有 /(/mathbf{C}_{2 /times 3} = /begin{bmatrix} 5 & 7 & 2 // 4 & 3 & 1 /end{bmatrix}/) 和 /(/mathbf{D}_{3 /times 1} = /begin{bmatrix} 1 // 5 // 6 /end{bmatrix}/)，则可以得出：

/[ /mathbf{C}/times /mathbf{D} = /begin{bmatrix} 5 & 7 & 2 // 4 & 3 & 1 /end{bmatrix}/times /begin{bmatrix} 1 // 5 // 6 /end{bmatrix} =/begin{bmatrix} 5 /cdot 1+ 7 /cdot 5+ 2/cdot 6 // 4/cdot 1+3/cdot 5+1/cdot 6 /end{bmatrix} =/begin{bmatrix} 52 // 25 /end{bmatrix} /]

与初等代数的乘法不同，矩阵的乘法并不满足交换律，即 /(/mathbf{A} /times /mathbf{B} /ne /mathbf{B} /times /mathbf{A}/)。但满足分配律，即 /((/mathbf{A} /times /mathbf{B}) /times /mathbf{C} = /mathbf{A} /times (/mathbf{B} /times /mathbf{C})/)。

再介绍两个特殊的矩阵：

1. 单元矩阵 /(/mathbf{I}/) 。它的特点是行数列数相等，且在对角线上值为 1，其他地方值为 0 。它的一个特性是与其他矩阵相乘都等于那个矩阵本身。一个 /(3/times 3/) 的单元矩阵示例：/[/mathbf{I}_{3 /times 3} = /begin{bmatrix} 1 & 0 & 0 // 0 & 1 & 0 // 0 & 0 & 1 /end{bmatrix}/]
2. 零矩阵。顾名思义就是全部元素都是 0 的矩阵。零矩阵乘以任何矩阵都为零矩阵，与任何矩阵相加都等于那个矩阵。

Python 示例：

>>> a * b
a * b
matrix([[ 4,  0, -1],
        [ 4, -2,  3],
        [ 6,  0,  0]])
>>> b * a
b * a
matrix([[ 1,  1,  2],
        [ 3,  0,  1],
        [ 1, -2,  1]])        
>>> c = np.matrix('5 7 2;4 3 1')
c = np.matrix('5 7 2;4 3 1')
>>> d = np.matrix('1;5;6')
d = np.matrix('1;5;6')
>>> c*d
c*d
matrix([[52],
        [25]])
>>> a * b * d
a * b * d
matrix([[-2],
        [12],
        [ 6]])
>>> a * (b * d)
a * (b * d)
matrix([[-2],
        [12],
        [ 6]])
>>> I = np.matrix('1 0 0;0 1 0;0 0 1')
I = np.matrix('1 0 0;0 1 0;0 0 1')
>>> a * I
a * I
matrix([[1, 0, 1],
        [1, 2, 1],
        [2, 1, 1]])
>>> I * a
I * a
matrix([[1, 0, 1],
        [1, 2, 1],
        [2, 1, 1]])
>>> a * z
a * z
matrix([[0, 0, 0],
        [0, 0, 0],
        [0, 0, 0]])
>>> b * z
b * z
matrix([[0, 0, 0],
        [0, 0, 0],
        [0, 0, 0]])
>>> c * z
c * z
matrix([[0, 0, 0],
        [0, 0, 0]])

除（求逆）

矩阵并没有一个直接叫除法的操作。但有个与之相似的运算，叫做求逆运算。

矩阵 /(/mathbf{A}/) 的逆 /(/mathbf{A}^{-1}/) 被定义为一个与 /(/mathbf{A}/) 相乘后能得到一个单元矩阵的矩阵。即：/(/mathbf{A} /times /mathbf{A}^{-1} = /mathbf{I}/)。求逆这个操作本身是可逆的，一个矩阵的逆的逆也是这个矩阵本身。因此 /(/mathbf{A}^{-1} /times /mathbf{A} = /mathbf{I}/)。根据这个特点我们可以推断出能求逆的矩阵，其行数和列数也必然相同。

为什么说这个求逆操作很像除等代数的除法呢？因为矩阵的逆很像数的倒数，一个数乘以它的倒数等于 1。而拿倒数与其他数相乘，就相当于被其他数除。

矩阵的求逆有很多种方法。常见的有伴随阵法、初等变换法、分块矩阵求逆法等。

伴随阵法

矩阵 /(/begin{bmatrix}A_{11} & A_{21} & /ldots & A_{n1} // A_{12} & A_{22} & /ldots & A_{n2} // /ldots & /ldots & /ldots & /ldots // A_{1n} & A_{2n} & /ldots & A_{nn} /end{bmatrix}/) 称为矩阵 /(/mathbf{A}/) 的伴随矩阵，记作 /(/mathbf{A}^{*}/) ，于是有 /(/mathbf{A}^{-1}=/frac{1}{|/mathbf{A}|}/mathbf{A}^{*}/)。

对于二阶矩阵，使用伴随阵法比较简单。

假定一个矩阵 /(/mathbf{M}=/begin{bmatrix} a & b // c & d /end{bmatrix}/)，则

/[/mathbf{M}^{-1}=/frac{1}{|/mathbf{M}|}/begin{bmatrix} d & -b // -c & a /end{bmatrix}/]

，其中 /(|/mathbf{M}|/) 称为矩阵 /(/mathbf{M}/) 的行列式：

/[|/mathbf{M}| = ad - bc/]

，而 /(/begin{bmatrix} d & -b // -c & a /end{bmatrix}/) 就是矩阵 /(/mathbf{M}/) 的伴随矩阵。

例如，对于矩阵 /(A = /begin{bmatrix} 5 & 7 // 3 & 2 /end{bmatrix}/)，那么有：

/[|/mathbf{A}|=5/cdot 2-7/cdot 3=-11/]

，则

/[/mathbf{A}^{ -1 }=/frac { 1 }{ -11 } /begin{bmatrix} 2 & -7 // -3 & 5 /end{bmatrix}=/begin{bmatrix} -/frac { 2 }{ 11 } & /frac { 7 }{ 11 } // /frac { 3 }{ 11 } & -/frac { 5 }{ 11 } /end{bmatrix}/]

验证一下 /(/mathbf{A} /times /mathbf{A}^{-1}/) 的值是否等于 /(/mathbf{I}/) ，有：

/[/mathbf{A}/times /mathbf{A}^{ -1 }=/begin{bmatrix} 5 & 7 // 3 & 2 /end{bmatrix}/times /begin{bmatrix} -/frac { 2 }{ 11 } & /frac { 7 }{ 11 } // /frac { 3 }{ 11 } & -/frac { 2 }{ 11 } /end{bmatrix}=/begin{bmatrix} 5/cdot /left( -/frac { 2 }{ 11 } /right) +7/cdot /frac { 3 }{ 11 } & 5/cdot /frac { 7 }{ 11 } +/left( -7/cdot /frac { 5 }{ 11 } /right) // 3/cdot /left( -/frac { 2 }{ 11 } /right) +2/cdot /frac { 3 }{ 11 } & 3/cdot /frac { 7 }{ 11 } +2/cdot /left( -/frac { 5 }{ 11 } /right) /end{bmatrix}=/begin{bmatrix} 1 & 0 // 0 & 1 /end{bmatrix} = /mathbf{I}/]

初等变换法

求元素为具体数字的矩阵的逆矩阵，常用初等变换法（又称为高斯·约当消去法）。用矩阵表示 $(/mathbf{A} /mathbf{I})/xrightarrow [ ]{ 初等变换 } (/mathbf{I} /mathbf{A}^{-1}) $ ，就是求逆矩阵的初等行变换法。/((/mathbf{A} /mathbf{I})/) 被称为矩阵 /(/mathbf{A}/) 的增广矩阵。

把上面定义中的“行”换成“列”，既得矩阵的初等列变换的定义。如果矩阵A经过有限次初等变换变成矩阵B，就称矩阵A与B等价。

三阶以上的伴随矩阵如果使用伴随阵法求逆，需要求9个或9个以上的代数余子式，以及一个三阶或三阶以上的行列式，过程比较繁琐。相比之下，使用初等变换就简单很多。

假定有三阶矩阵 /({ /mathbf{A} }_{ 3 /times 3 }=/begin{bmatrix} 1 & 0 & 1 // 1 & 2 & 1 // 2 & 1 & 1 /end{bmatrix}/) ，则：

/[ /begin{aligned} /begin{bmatrix}/mathbf{A} /mathbf{I}/end{bmatrix} & /rightarrow /begin{bmatrix} 1 & 0 & 1 & 1 & 0 & 0 // 1 & 2 & 1 & 0 & 1 & 0 // 2 & 1 & 1 & 0 & 0 & 1 /end{bmatrix} /rightarrow /begin{bmatrix} 1 & 0 & 1 & 1 & 0 & 0 // 0 & 2 & 0 & -1 & 1 & 0 // 2 & 1 & 1 & 0 & 0 & 1 /end{bmatrix} /rightarrow /begin{bmatrix} 1 & 0 & 1 & 1 & 0 & 0 // 0 & 1 & 0 & -0.5 & 0.5 & 0 // 2 & 1 & 1 & 0 & 0 & 1 /end{bmatrix}// & /rightarrow /begin{bmatrix} 1 & 0 & 1 & 1 & 0 & 0 // 0 & 1 & 0 & -0.5 & 0.5 & 0 // 1 & 1 & 0 & -1 & 0 & 1 /end{bmatrix} /rightarrow /begin{bmatrix} 1 & 0 & 1 & 1 & 0 & 0 // 0 & 1 & 0 & -0.5 & 0.5 & 0 // 1 & 0 & 0 & -0.5 & -0.5 & 1 /end{bmatrix} /rightarrow /begin{bmatrix} 0 & 0 & 1 & 1.5 & 0.5 & -1 // 0 & 1 & 0 & 0 & 0.5 & 0 // 1 & 0 & 0 & -0.5 & -0.5 & 1 /end{bmatrix}// &/rightarrow /begin{bmatrix} 1 & 0 & 0 & -0.5 & -0.5 & 1 // 0 & 1 & 0 & -0.5 & 0.5 & 0 // 0 & 0 & 1 & 1.5 & 0.5 & -1 /end{bmatrix} /end{aligned} /]

因此

/[/mathbf{A}^{-1}=/begin{bmatrix}-0.5 & -0.5 & 1 // -0.5 & 0.5 & 0 // 1.5 & 0.5 & -1/end{bmatrix}/]

奇异矩阵

要注意的是， 矩阵并不一定都可逆的 。从定义来看，只要矩阵 /(/mathbf{M}/) 的行列式 /(|/mathbf{M}|/) 为 0 ，则 /[/mathbf{M}^{-1}=/frac{1}{|/mathbf{M}|}/begin{bmatrix} d & -b // -c & a /end{bmatrix}/] 的值就无定义。我们把这种矩阵叫做 奇异矩阵 。

例如矩阵 /(/begin{bmatrix}0 & 0// 0 & 1/end{bmatrix}/) ，其行列式的值为 /(0 /cdot 1 - 0 /cdot 0 = 0/) ，因此无法求逆。

Python 求逆示例：

>>> a = np.matrix('1 0 1; 1 2 1; 2 1 1')
a = np.matrix('1 0 1; 1 2 1; 2 1 1')
>>> a.I
a.I
matrix([[-0.5, -0.5,  1. ],
        [-0.5,  0.5,  0. ],
        [ 1.5,  0.5, -1. ]])
>>> a * a.I
a * a.I
matrix([[ 1.,  0.,  0.],
        [ 0.,  1.,  0.],
        [ 0.,  0.,  1.]]
>>> a.I * a
a.I * a
matrix([[ 1.,  0.,  0.],
        [ 0.,  1.,  0.],
        [ 0.,  0.,  1.]])
>>> f = np.matrix('0 1;0 0')
f = np.matrix('0 1;0 0')
>>> f.I
f.I
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "/Library/Python/2.7/site-packages/numpy/matrixlib/defmatrix.py", line 972, in getI
    return asmatrix(func(self))
  File "/Library/Python/2.7/site-packages/numpy/linalg/linalg.py", line 526, in inv
    ainv = _umath_linalg.inv(a, signature=signature, extobj=extobj)
  File "/Library/Python/2.7/site-packages/numpy/linalg/linalg.py", line 90, in _raise_linalgerror_singular
    raise LinAlgError("Singular matrix")
numpy.linalg.linalg.LinAlgError: Singular matrix

应用举例

矩阵是一种非常通用的数据表示方法，只要能用矩阵来表示数据，就能够用矩阵的这套运算来解决问题。下面列举几种常见的数学问题，它们都能够使用矩阵的思路来解决。

求解方程组

例如一个二元方程组

/[/left/{ /begin{eqnarray} 3x+2y & = & 7 // -x+y & = & 1 /end{eqnarray} /right. /]

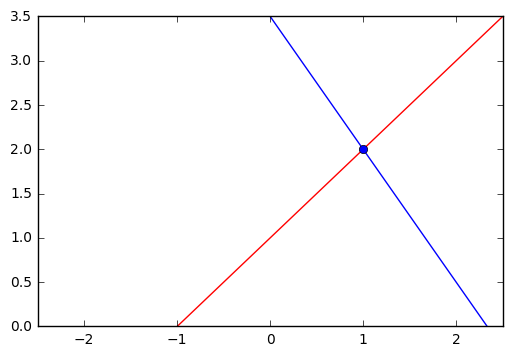
可以用矩阵表示成：

/[/begin{bmatrix} 3 & 2 // -1 & 1 /end{bmatrix} /begin{bmatrix} x // y /end{bmatrix} = /begin{bmatrix} 7// 1 /end{bmatrix} /]

设公式里的 /(/begin{bmatrix} 3 & 2 // -1 & 1/end{bmatrix}/) 为矩阵 /(A/)，将等式两边左乘一个 /(A/) 的逆得到：

/[ /begin{aligned} A^{-1}A /begin{bmatrix} x // y /end{bmatrix} &= A^{-1} /begin{bmatrix} 7// 1 /end{bmatrix}/// &= /frac{1}{|A|}/begin{bmatrix}1 & -2 // 1 & 3/end{bmatrix} /begin{bmatrix} 7// 1 /end{bmatrix}/// &= /frac{1}{5}/begin{bmatrix}1 & -2 // 1 & 3/end{bmatrix} /begin{bmatrix} 7// 1 /end{bmatrix}/// &= /frac{1}{5}/begin{bmatrix}5 // 10/end{bmatrix} /end{aligned} /]

因此： $ /begin{bmatrix}x // y/end{bmatrix} = /begin{bmatrix}1 // 2/end{bmatrix} $

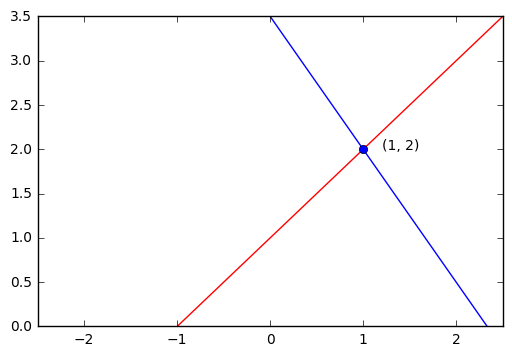
虽然这个例子给出的方法用于二元一次矩阵求解还不如直接用初中就学到的消元法，但矩阵的好处在于对于更高维的数据，比如有成百上千个未知数，这个解法依然有效。

求向量组合

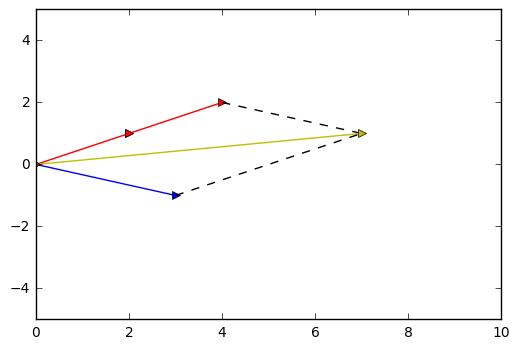
假设有向量 /(/vec { a } = /begin{bmatrix} 3 // -1 /end{bmatrix}/) ，/(/vec { b } = /begin{bmatrix} 2 // 1 /end{bmatrix}/) ，求二者如何组合成向量 /(/vec { c } = /begin{bmatrix} 7 // 1 /end{bmatrix}/) ？

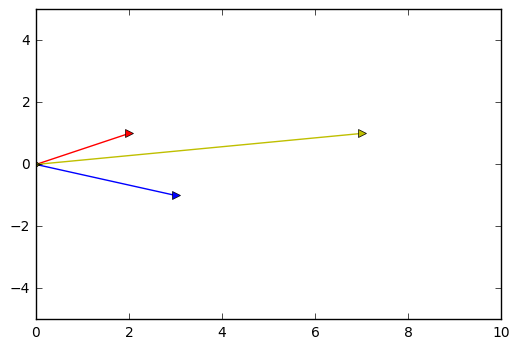
如果用 /(x/) 和 /(y/) 分别表示两个向量的倍数，这个问题就同样可以用矩阵表示成：

/[/begin{bmatrix} 3 // -1 /end{bmatrix} x + /begin{bmatrix} 2 // 1 /end{bmatrix} y = /begin{bmatrix} 7// 1 /end{bmatrix} /]

这样就得到了一个和上一个问题完全同构的问题，使用相同解法解决得出 $ /begin{bmatrix}x // y/end{bmatrix} = /begin{bmatrix}1 // 2/end{bmatrix} $。

深入阅读

1. 逆矩阵的几种求法与解析