转载

纯CSS画六围图

最近做游戏资料经常要描述六围，现在比较流行的做法就是用六围图，但是资料库系统限制导致外挂JS库或者JS代码比较麻烦，何况秉承着能用CSS绝不用JS的思路，于是想着看能不能用CSS做六围图…

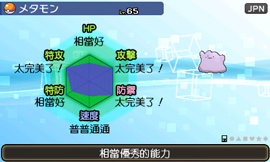
纯CSS画六围图

做出来差不多就是这样了：

在 CodePen 上查看纯CSS六边形雷达图 ( @hikarievo )。

顺带一提，这玩意儿的学名叫雷达图…我搜什么六边形图标啊六围图啊都搜不到快急死我了……

基本思路

六围图通常是一个不规则六边形（6V选手一边去），我们已知的值就是顶点到中心的距离，而将所有的顶点与中心点连接起来之后，我们就得到了6个已知的三角形（已知两个邻边长度及其夹角就可以确定一个三角形…如果背过三角形相似/全等规则的话大概会想起SAS）。

CSS画三角本身并不困难，使用一个DOM元素加上一些CSS代码就可以画出任意三角形。但是这些三角形要么无法固定夹角度数，要么无法满足邻边长度的要求（简单来说，就是无法画出钝角三角形），所以我将目光转移到了CSS transform 。如果先画出一个邻边长度满足要求的直角三角形，再把直角扭成所需圆心角的度数不就OK了嘛。一开始我想用 skew() 来解决这个问题，但是 skew() 是斜切，也就是说，在保持DOM面积不变（高度不变）的情况下，倾斜元素。但是我需要的是 保持两边边长不变，倾斜元素 …所以已知的CSS transform 简易方法都阵亡了。于是只好祭出 transform 的最终杀器—— matrix() （

~~黑客帝国~~ 矩阵变换），理论上 matrix()

可以完成任何线性变换，非常适合这种场合。

基本操作思路如下：

按照给定边长绘制直角三角形。
使用 matrix() 将直角三角形的直角扭成所需的圆心角。
依次旋转所得的三角形。

计算矩阵

…思路就是要跳跃，画直角三角形随便摆弄一下上面的生成器就能搞定了。问题在于矩阵要怎么办…矩阵变换听起来挺复杂的，其实只要搞明白写法就OK了。

matrix() 需要提供6个参数，从a到f，转换成矩阵如下图：

转换成我们熟悉的方式写成方程组的话，就是：

x’=ax+cy+e

y’=bx+dy+f

然后我们的变换是这样的（画的平行四边形，真正的三角形只有它的一半…这个工具还不太会用2333）：

在这里我出了点小小的思路上的问题，在准备这篇文章的时候才发现…主要是我还保留着 skew() 的思路，而且当时心想着反正都是转，转几圈都是转…导致多转了一次，这个回头说。

根据上面的图解出来（解方程的时候发生了一场惨剧…按习惯画坐标轴都是右上为正，左下为负，可是我忘了！忘了！CSS渲染下的Y轴方向是向下的！向下的！！导致我对着一个方程算了俩钟头，怎么算都是反的！！）：

x’=x-Sinθ y

y’=Cosθ y

matrix(1,0,-Sinθ,Cosθ,0,0)

因为六边形的圆心角是60度，所以θ是30度。代入得到 matrix(1,0,-0.5,(√3)/2)

旋转代入

CSS transform 有一个 transform-origin 属性，可以规定元素变换的原点。对于前面所示的情况，显然是以我们的已知角——左下角为原点代入最合适。CSS旋转本身可以用 rotate() ，但是我直接测试的结果是它总转不到该转的地方，一不做二不休，干脆直接乘进去算了…

旋转的矩阵是这样的，角度为逆时针：

!(来自PolymathProgrammer)[ http://polymathprogrammer.com/images/blog/200809/rotationmatrix2d.png ]

因此对应六围图右上角那个三角的位置，旋转角度应该是30°，接下来的三角形依次旋转60°就可以了

原文 http://hikarievo.me/2017/02/02/draw-pure-css-hexagon-radar-chart/

正文到此结束