机器学习的数学基础：线性代数进阶篇

前言

在前面两篇文章中，我简要概括了线性代数中两个最基本的数据表达方式：矩阵 和向量。有了这两个数学工具作为基础，我们可以再进一步，讨论下面一些内容：

1. 如何求解线性空间的基？
2. 向量的子空间、零空间、列空间、行空间、左零空间都是什么东西？怎么求解？
3. 如何用线性代数的知识来拟合数据？
4. 机器学习、图像处理中常见的“特征向量”究竟是什么东西？它和变换矩阵有什么联系？

本篇文章将作为线性代数子系列的最终篇。

阶梯形矩阵

阶梯形矩阵是一类非常实用的工具，可以帮助我们求解出线性空间的基，这就能用在诸如计算解不唯一的方程组之类的问题上。

阶梯形矩阵

若矩阵 /(/mathbf{A}/) 满足两条件：

1. 若有零行（元素全为0的行），则零行应在最下方；
2. 非零首元（即非零行的第一个不为零的元素）的列标号随行标号的增加而严格递增。

则称此矩阵 /(/mathbf{A}/) 为阶梯形矩阵。

示例：

/[ /begin{bmatrix} 2 & 0 & 2 & 1 // 0 & 5 & 2 & -2 // 0 & 0 & 3 & 2 // 0 & 0 & 0 & 0 /end{bmatrix} /]

行简化阶梯形矩阵

若矩阵 /(/mathbf{A}/) 满足两条件：

1. 它是阶梯形矩阵；
2. 非零首元所在的列除了非零首元外，其余元素全为0。

则称此矩阵 /(/mathbf{A}/) 为行简化阶梯形矩阵。

示例：

/[ /begin{bmatrix} 2 & 0 & 2 & 1 // 0 & 5 & 2 & -2 // 0 & 0 & 3 & 2 // 0 & 0 & 0 & 0 /end{bmatrix} /]

行最简形矩阵

若矩阵 /(/mathbf{A}/) 满足两条件：

1. 它是行简化阶梯形矩阵；
2. 非零首元都为1

则称此矩阵 /(/mathbf{A}/) 为行最简形矩阵。

将矩阵化简成行最简阶梯形

对如下矩阵

/[ /begin{bmatrix} 1 & 2 & 1 & 1 & 7// 1 & 2 & 2 & -1 & 12// 2 & 4 & 0 & 6 & 4 /end{bmatrix} /]

，使用初等变换可以将这个矩阵转换成如下的形式：

/[ /begin{bmatrix} 1 & 2 & 1 & 1 & 7// 1 & 2 & 2 & -1 & 12// 2 & 4 & 0 & 6 & 4 /end{bmatrix} /rightarrow /begin{bmatrix} 1 & 2 & 1 & 1 & 7// 0 & 0 & 1 & -2 & 5// 2 & 4 & 0 & 6 & 4 /end{bmatrix} /rightarrow /begin{bmatrix} 1 & 2 & 1 & 1 & 7// 0 & 0 & 1 & -2 & 5// 0 & 0 & -2 & 4 & -10 /end{bmatrix} /rightarrow /begin{bmatrix} 1 & 2 & 1 & 1 & 7// 0 & 0 & 1 & -2 & 5// 0 & 0 & 0 & 0 & 0 /end{bmatrix} /rightarrow /begin{bmatrix} 1 & 2 & 0 & 3 & 2// 0 & 0 & 1 & -2 & 5// 0 & 0 & 0 & 0 & 0 /end{bmatrix} /]

行最简形非常实用。例如，对于下面的方程组：

/[/left/{ /begin{eqnarray} x_1 + 2x_2 + x_3 + x_4 &=& 7 /// x_1 + 2x_2 + 2x_3 - x_4 &=& 12 /// 2x_1 + 4x_2 + 6x_4 &=& 4 /end{eqnarray} /right. /]

只有三个方程，肯定无法求解出四个未知数（此时如果在用 numpy.linalg.solve 求解这个矩阵会引发 LinAlgError ），但是通过化成行最简形，我们可以进一步找出变量的限制关系。先将方程组表达成增广矩阵形式：

/[ /begin{bmatrix} 1 & 2 & 1 & 1 & 7// 1 & 2 & 2 & -1 & 12// 2 & 4 & 0 & 6 & 4 /end{bmatrix} /]

这个矩阵和完全和我们上一步给出的矩阵相同，因此其行简化阶梯性就是

/[ /begin{bmatrix} 1 & 2 & 0 & 3 & 2// 0 & 0 & 1 & -2 & 5// 0 & 0 & 0 & 0 & 0 /end{bmatrix} /]

对于方程组，非0首元位置对应的变量就叫做 主元变量 ，其他的变量就叫做 自由变量 。例如上面的行最简形，/(x_1/) 和 /(x_3/) 是首元变量，/(x_2/) 和 /(x_4/) 就是自由变量。我们可以将方程改写成下面的形式：

/[ /left/{ /begin{eqnarray} x_1 &=& 2 - 2x_2 - 3x_4 /// x_3 &=& 5 + 2x_4 /end{eqnarray} /right. /]

然后可以得到：

/[ /begin{bmatrix} x_{ 1 } // x_{ 2 } // x_{ 3 } // x_{ 4 } /end{bmatrix}=/begin{bmatrix} 2 // 0 // 5 // 0 /end{bmatrix}+x_{ 2 }/underbrace { /begin{bmatrix} -2 // 1 // 0 // 0 /end{bmatrix} }_{ /vec{/mathbf{a}} } +x_{ 4 }/underbrace{/begin{bmatrix} -3 // 0 // 2 // 1 /end{bmatrix}}_{/vec{/mathbf{b}}} /]

观察这个结果，方程组的解集就是向量 /(/vec{/mathbf{a}}/) 和向量 /(/vec{/mathbf{b}}/) 的线性组合。这两个向量张成了 /(/mathbb{R}^1/) 中的一个平面。

线性子空间

在前面的内容中我们已经多少涉及到了一些关于空间、张成空间的知识了。有时候我们需要从一个空间 /(K/) 里头挑出一些向量张成一个新的空间 /(/mathbf{W}/) ，这个空间 /(/mathbf{W}/) 就是原来的向量 /(/mathbf{K}/) 的子空间。

子空间的引入有助于我们更专注于某类线性组合，从中找出这些子空间的特点，以及与原来的空间的关系。下面将列举几种典型的子空间。

零空间

矩阵 /(/mathbf{A}/) 的零空间 /(N(/mathbf{A})/) 就是由满足 /(/mathbf{A}/vec{/mathbf{x}}=0/) 的所有向量 /(/vec{/mathbf{x}}/) 的集合。

要求解一个矩阵的零空间，可以先将其化简成行最简形。例如矩阵 $/mathbf{A} = /begin{bmatrix} 1 & 1 & 1 & 1 // 1 & 2 & 3 & 4 // 4 & 3 & 2 & 1 /end{bmatrix} $，为了计算零空间，可以写出如下的等式：

/[/begin{bmatrix} 1 & 1 & 1 & 1 // 1 & 2 & 3 & 4 // 4 & 3 & 2 & 1 /end{bmatrix} /begin{bmatrix} x_1 // x_2 // x_3 // x_4 /end{bmatrix} = /begin{bmatrix} 0 // 0 // 0 /end{bmatrix}/]

展开得到如下的方程组：

/[ /left/{ /begin{eqnarray} x_1 + x_2 + x_3 + x_4 &=& 0 /// x_1 + 2x_2 + 3x_3 + 4x_4 &=& 0 /// 4x_1 + 3x_2 + 2x_4 + x_4 &=& 0 /end{eqnarray} /right. /]

参考一节里介绍的方法，先把上面的方程组表示成增广矩阵：

/[ /begin{bmatrix} 1 & 1 & 1 & 1 & 0 // 1 & 2 & 3 & 4 & 0 // 4 & 3 & 2 & 1 & 0 /end{bmatrix} /]

然后将其转换成行最简形：

/[ /begin{bmatrix} 1 & 0 & -1 & -2 & 0 // 0 & 1 & 2 & 3 & 0 // 0 & 0 & 0 & 0 & 0 /end{bmatrix} /]

最终求解得到：

/[ /begin{bmatrix} x_{ 1 } // x_{ 2 } // x_{ 3 } // x_{ 4 } /end{bmatrix}=x_{ 3 }/underbrace { /begin{bmatrix} 1 // -2 // 1 // 0 /end{bmatrix} }_{ /vec{/mathbf{a}} } +x_{ 4 }/underbrace{/begin{bmatrix} 2 // -3 // 0 // 1 /end{bmatrix}}_{/vec{/mathbf{b}}} /]

因此矩阵 /(/mathbf{A}/) 的零空间就是由上式中的 /(/vec{/mathbf{a}}/) 向量和 /(/vec{/mathbf{b}}/) 向量张成的空间。即

/[N(/mathbf{A}) = span/left(/begin{bmatrix} 1 // -2 // 1 // 0 /end{bmatrix} /begin{bmatrix} 2 // -3 // 0 // 1 /end{bmatrix}/right)/]

另外，上面得到的这个行最简形有两个自由变量，就称矩阵 /(/mathbf{A}/) 的 零度 为 2。零度等于 /(/mathbf{A}/vec{/mathbf{x}} = 0/) 化成行最简形后自由变量的个数。

列空间

矩阵的列空间就是由每一列的向量张成的空间。对于矩阵 /(/underset { m/times n }{ /mathbf{A} } =/begin{bmatrix} /underbrace { /begin{bmatrix} a_{ 11 } // a_{ 21 } // /ldots // a_{ m1 } /end{bmatrix} }_{ /vec { /mathbf{ V }_{ 1 } } } & /underbrace { /begin{bmatrix} a_{ 12 } // a_{ 22 } ///ldots // a_{ m2 } /end{bmatrix} }_{ /vec { /mathbf{ V_{ 2 } } } } & /ldots & /underbrace { /begin{bmatrix} a_{ 1n } // a_{ 2n } // /ldots // a_{ mn } /end{bmatrix} }_{ /vec { /mathbf{ V_{ n } } } } /end{bmatrix}/)，那么矩阵 /(/mathbf{A}/) 的列空间就是

/[C(/mathbf{A}) = span(/vec{v_1}, /vec{v_2}, /ldots, /vec{v_n})/]

例如，矩阵 /(/mathbf{A} = /begin{bmatrix}1 & 1 & 1 & 1 // 1 & 2 & 3 & 4 //4 & 3 & 2 & 1/end{bmatrix}/) 的列空间是 /(C(/mathbf{A}) = span/left(/begin{bmatrix}1 // 1 // 4/end{bmatrix}/begin{bmatrix}1 // 2 // 3/end{bmatrix}/begin{bmatrix}1 // 3 // 2/end{bmatrix}/begin{bmatrix}1 // 4 // 1/end{bmatrix}/right)/)

把一个矩阵化成行最简形后，这个矩阵的不相关主列（基底）的个数就称为矩阵的 秩 （Rank），或者叫维数。

例如，上面的矩阵 /(/mathbf{A}/) 化成最简形矩阵是（参考上节的化简结果）：

/[ /begin{bmatrix} 1 & 0 & -1 & -2 // 0 & 1 & 2 & 3 // 0 & 0 & 0 & 0 /end{bmatrix} /]

从结果可以看出这个矩阵的主列有 2 个，而且是线性无关的。所以矩阵 /(/mathbf{A}/) 的秩为 2 ，即 /(rank(/mathbf{A}) = 2/)。

在 Python 中，可以使用 Numpy 包中的 linalg.matrix_rank 方法计算矩阵的秩：

a = np.matrix('1 1 1 1;1 2 3 4;4 3 2 1')
print np.linalg.matrix_rank(a)  # 2

import numpy as np
a = np.matrix('1 1 1 1;1 2 3 4; 0 0 1 0')
print a.ndim  # 2（维度）
print np.linalg.matrix_rank(a)  # 3（秩）

行空间

有了列空间的定义，行空间顾名思义就是矩阵的每一行转置得到的向量张成的子空间，也就是矩阵的转置的列空间，记为 /(R(/mathbf{A}) = C(/mathbf{A}^T)/)。

例如，矩阵 /(/mathbf{A} = /begin{bmatrix}1 & 1 & 1 & 1 // 1 & 2 & 3 & 4 //4 & 3 & 2 & 1/end{bmatrix}/) 的行空间是 /(R(/mathbf{A}) = C(/mathbf{A}^T) = span/left(/begin{bmatrix}1 // 1 // 1 // 1/end{bmatrix}/begin{bmatrix}1 // 2 // 3 // 4/end{bmatrix}/begin{bmatrix}4 // 3 // 2 // 1/end{bmatrix}/right)/)。

左零空间

矩阵 /(/mathbf{A}/) 的左零空间是 /(/mathbf{A}/) 的转置的零空间。即：

/[N(/mathbf{A}^T) = /left/{ /vec{/mathbf{x}} | /mathbf{A}^{T} /vec{/mathbf{x}} = /vec{/mathbf{0}} /right/} = /left/{ /vec{/mathbf{x}} | /vec{/mathbf{x}}^{T} /mathbf{A} = /vec{/mathbf{0}}^{T} /right/}/]

例如，矩阵 /(/mathbf{B} = /begin{bmatrix}1 & 1 & 4 // 1 & 2 & 3 //1 & 4 & 2// 1 & 3 & 1/end{bmatrix}/) 的转置是矩阵 /(/mathbf{A} = /mathbf{A} = /begin{bmatrix}1 & 1 & 1 & 1 // 1 & 2 & 3 & 4 //4 & 3 & 2 & 1/end{bmatrix}/) ，因此左零空间是 /(N(/mathbf{B^T}) = N(/mathbf{A}) = span/left(/begin{bmatrix} 1 // -2 // 1 // 0 /end{bmatrix} /begin{bmatrix} 2 // -3 // 0 // 1 /end{bmatrix}/right)/)

由于转置是对称的，所以矩阵 /(/mathbf{A}/) 的转置的左零空间也是矩阵 /(/mathbf{A}/) 的零空间。

子空间的正交补

假设 /(/mathbf{V}/) 是 /(/mathbb{R}^n/) 的一个子空间，那么 /(/mathbf{V}/) 的正交补 /(/mathbf{V}^{/bot}/) 也是一个子空间，定义为 /(/left/{/vec{/mathbf{x}} | /vec{/mathbf{x}} /vec{/mathbf{v}}=0/right/}/)，也即是 /(/mathbb{R}^{n}/) 中所有正交于 /(/mathbf{V}/) 的向量所组成的子空间。

由于正交是对称的，所以正交补也是对称的。一个子空间的正交补的正交补依然等于这个子空间。

矩阵的零空间是行空间的正交补，即 /(N(/mathbf{A}) = R(/mathbf{A})^{/bot}/)。反过来，矩阵的左零空间是列空间的正交补，即 /(N(/mathbf{B}^T) = C(/mathbf{B})^{/bot}/)。

最小二乘逼近

最小二乘法是一个实用的数学工具，利用它可以在方程无解的情况下给出近似解。在机器学习中，最小二乘逼近也是一个重要的拟合方法。

假设有一个方程

/[ /underset{n/times k}{/mathbf{A}}/vec{/mathbf{x}} = /vec{/mathbf{b}} /]

无解。把上式写成：

/[ /vec{a_1}/vec{/mathbf{x}} + /vec{a_2}/vec{/mathbf{x}} + /ldots + /vec{a_k}/vec{/mathbf{x}} = /vec{/mathbf{b}} /]

无解就意味着 /(/mathbf{A}/) 的所有列向量的张成空间不包括向量 /(/vec{/mathbf{b}}/) 。即 /(/vec{/mathbf{b}} /notin span(C(/mathbf{A}))/)。

我们可以通过最小二乘法求解出近似解。即是要让找出一些向量 /(/vec{/mathbf{x}^*}/) 使得 /(/left/|/vec{/mathbf{b}}-/mathbf{A}/vec{/mathbf{x}^*}/right/|/) 最小。用向量 /(/vec{/mathbf{V}}/) 代表 /(/mathbf{A}/vec{/mathbf{x}^*}/) ，有：

/[ /left/| /begin{bmatrix} /vec{b_1}-/vec{v_1}// /vec{b_2}-/vec{v_2}// /ldots// /vec{b_n}-/vec{v_n}// /end{bmatrix} /right/|^2 = (b_1-v_1)^2 + (b_2-v_2)^2 + /ldots + (b_n-v_n)^2 /]

把这个值最小化的过程就叫做 最小二乘逼近 。

如何求出 /(/mathbf{A}/vec{/mathbf{x}^*}/) 这个近似值呢？从几何上考虑，列空间可以看成空间中张成的一个平面，而向量 /(/vec{/mathbf{b}}/) 并不落在这个平面上。但我们知道，在这个平面上与向量 /(/vec{/mathbf{b}}/) 最接近的向量就是它的投影！所以，

/[ /mathbf{A}/vec{/mathbf{x}^*} = Proj_{C(/mathbf{A})}/vec{/mathbf{b}} /]

直接计算 /(Proj_{C(/mathbf{A})}/vec{/mathbf{b}}/) 并不简单。不过，/(/vec{/mathbf{b}}-/mathbf{A}/vec{/mathbf{x}}/) 其实就是 /(/mathbf{A}/vec{/mathbf{x}}/) 的正交补，所以一个简单的求解方法是将原来无解的方程左乘一个 /(/mathbf{A}/) 的转置再求解：

/[ /mathbf{A}^T/mathbf{A}/vec{/mathbf{x}^*} = /mathbf{A}^T/vec{/mathbf{b}} /]

得出的解就是原方程的近似解。

实例1：求解方程

问题：求解如下方程组

/[ /left/{ /begin{eqnarray} x + y &=& 3 /// x - y &=& -2 /// y &=& 1 /end{eqnarray} /right. /]

将三个方程表示的直线画出来，可以看出这三条直线并没有交点：

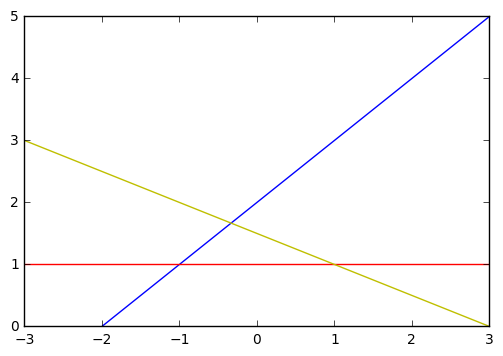
如何找出一个与三条直线距离最近的一个点呢？这时候我们的最小二乘逼近就派上用场了。

先将方程写成矩阵和向量的形式：

/[ /underbrace{ /begin{bmatrix} 1 & 1 // 1 & -1 // 0 & 1 /end{bmatrix} }_{/mathbf{A}} /underbrace{ /begin{bmatrix} x // y /end{bmatrix} }_{/vec{/mathbf{x}}} = /underbrace{ /begin{bmatrix} 3 // 2 // 1 /end{bmatrix} }_{/vec{/mathbf{b}}} /]

这个等式的最小二乘逼近就是：

/[ /begin{align} /begin{bmatrix} 1 & 1 & 0 // 1 & -1 & 1// /end{bmatrix} /begin{bmatrix} 1 & 1 // 1 & -1 // 0 & 1 /end{bmatrix} /begin{bmatrix} x^* // y^* /end{bmatrix} & = /begin{bmatrix} 1 & 1 & 0 // 1 & -1 & 1// /end{bmatrix} /begin{bmatrix} 3 // 2 // 1 /end{bmatrix} /// /begin{bmatrix} 2 & 0 // 0 & 3 /end{bmatrix} /begin{bmatrix} x^* // y^* /end{bmatrix} & = /begin{bmatrix} 5 // 2 /end{bmatrix} /end{align} /]

由于是二阶方程，可以很容易求出矩阵 /(/begin{bmatrix}2 & 0 // 0 & 3/end{bmatrix}/) 的逆是 /(/begin{bmatrix}/frac{1}{2} & 0 // 0 & /frac{1}{3}/end{bmatrix}/)，所以：

/[ /begin{bmatrix} x^* // y^* /end{bmatrix} = /begin{bmatrix}/frac{1}{2} & 0 // 0 & /frac{1}{3}/end{bmatrix} /begin{bmatrix} 5 // 2 /end{bmatrix} = /begin{bmatrix} /frac{5}{2} // /frac{2}{3} /end{bmatrix} /]

因此 /(/begin{bmatrix}/frac{5}{2} ///frac{2}{3}/end{bmatrix}/) 就是方程组的近似解。

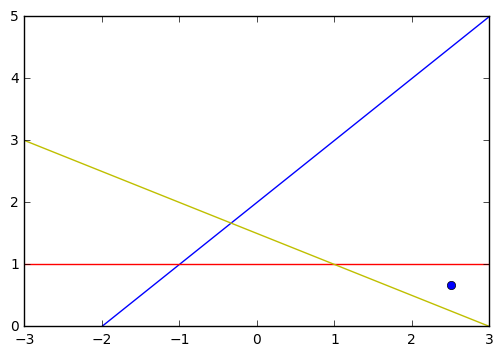
在 Python 中，可以使用 numpy.linalg.lstsq 方法来求解最小二乘逼近。

>>> a = np.array([[1, 1], [1, -1], [0, 1]])
>>> b = np.array([3, 2, 1])
>>> x = np.linalg.lstsq(a,b)
>>> print x
(array([ 2.5       ,  0.66666667]), array([ 0.16666667]), 2, array([ 1.73205081,  1.41421356]))

numpy.linalg.lstsq 的返回包括四个部分：

1. 最小二乘逼近解。如果 b 是二维的，那么这个逼近的结果有多个列，每一列是一个逼近解。对于上例，逼近解就是 /(/begin{bmatrix}2.5 // 0.66666667 /end{bmatrix}/) 。
2. 残差。即每一个 b - a*x 的长度的和。对于上例，残差是 0.16666667 。
3. 矩阵 a 的秩。对于上例，矩阵 a 的秩为 2 。
4. 矩阵 a 的奇异值。对于上例，矩阵 a 的奇异值为 /(/begin{bmatrix}1.73205081 // 1.41421356/end{bmatrix}/)

实例2：线性回归

问题：给定4个坐标点 /((-1, 0)/), /((0, 1)/), /((1, 2)/), /((2, 1)/) ，求一条经过这些点的直线 /(y=mx+b/)。

将四个点画图如下：

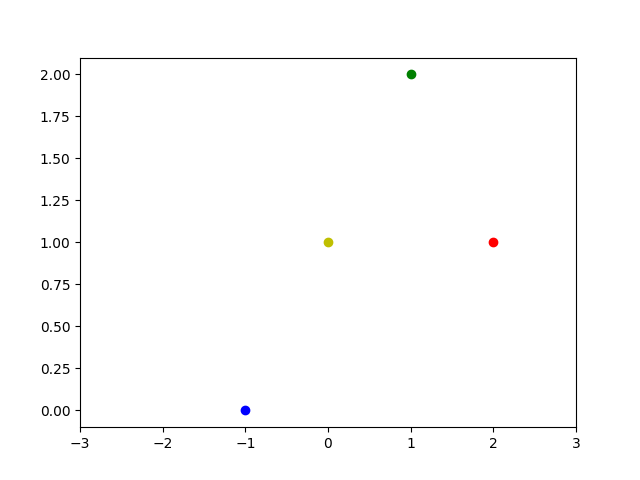
显然这样的直线并不存在。然而我们能够使用最小二乘逼近，找到一条尽可能接近这些点的直线。将四个点表示成方程组的形式：

/[ /left/{ /begin{eqnarray} f(-1) &= -m + b = 0/// f(0) &= 0 + b = 1/// f(1) &= m + b = 2/// f(2) &= 2m + b = 1 /end{eqnarray} /right. /]

还是那个套路，将方程组表示成矩阵和向量的形式：

/[ /underbrace{ /begin{bmatrix} -1 & 1 // 0 & 1 // 1 & 1 // 2 & 1 /end{bmatrix} }_{/mathbf{A}} /underbrace{ /begin{bmatrix} m// b /end{bmatrix} }_{/vec{/mathbf{x}}} = /underbrace{ /begin{bmatrix} 0// 1// 2// 1 /end{bmatrix} }_{/vec{/mathbf{b}}} /]

这个等式的最小二乘逼近就是：

/[ /begin{align} /begin{bmatrix} -1 & 0 & 1 & 2 // 1 & 1 & 1 & 1 /end{bmatrix} /begin{bmatrix} -1 & 1 // 0 & 1 // 1 & 1 // 2 & 1 /end{bmatrix} /begin{bmatrix} m^*// b^* /end{bmatrix} &= /begin{bmatrix} -1 & 0 & 1 & 2 // 1 & 1 & 1 & 1 /end{bmatrix} /begin{bmatrix} 0// 1// 2// 1 /end{bmatrix}/// /begin{bmatrix} 6 & 2 // 2 & 4 /end{bmatrix} /begin{bmatrix} m^*// b^* /end{bmatrix} &= /begin{bmatrix} 4// 4 /end{bmatrix} /end{align} /]

容易求得 /(/begin{bmatrix}6 & 2//2 & 4/end{bmatrix}/) 的逆为 /(/frac{1}{20}/begin{bmatrix}4 & -2//-2 & 6/end{bmatrix}/)，因此

/[/begin{bmatrix}m^*//b^*/end{bmatrix} = /frac{1}{20}/begin{bmatrix}4 & -2//-2 & 6/end{bmatrix}/begin{bmatrix}4 // 4/end{bmatrix} = /frac{1}{20}/begin{bmatrix}8 // 16/end{bmatrix} = /begin{bmatrix}/frac{2}{5} // /frac{4}{5}/end{bmatrix}/]

将直线 /(y = /frac{2}{5}x + /frac{4}{5}/) 绘图如下所示：

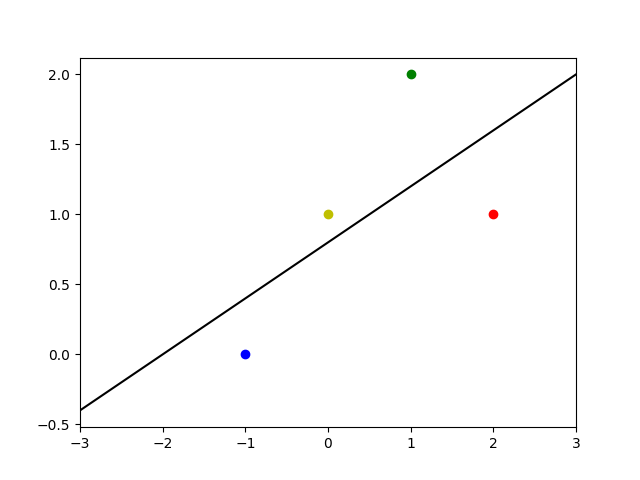
这就是所求的直线的近似解。

Python 示例如下：

>>> a = np.matrix('-1 1;0 1;1 1;2 1')
>>> b = np.array([0, 1, 2, 1])
>>> x = np.linalg.lstsq(a, b)
>>> print x
(array([ 0.4,  0.8]), array([ 1.2]), 2, array([ 2.68999405,  1.66250775]))

特征向量

“特征”在模式识别和图像处理中是非常常见的一个词汇。我们要认识和描绘一件事物，首先得找出这个事物的特征。同样的道理，要让计算机识别一件事物，首先就要让计算机学会理解或者抽象出事物的特征。什么样的东西能当成特征呢？那必须是能“放之四海皆准”的依据，不论个体如何变换，都能从中找到这类群体共有的特点。例如，计算机视觉中常用的SIFT 特征点 是一种很经典的用于视觉跟踪的特征点，即使被跟踪的物体的尺度、角度发生了变化，这种特征点依然能够找到关联。在机器学习中， 特征向量选取也是整个机器学习系统中非常重要的一步。

在线性代数中，“特征” 就是一种更抽象的描述。我们知道，矩阵乘法对应了一个变换，是把任意一个向量变成另一个方向或长度都大多不同的新向量。在这个变换的过程中，原向量主要发生旋转、伸缩的变化。如果矩阵对某一个向量或某些向量只发生伸缩（尺度）变换，而没有产生旋转的效果（也就意味着张成的子空间没有发生改变），这样的向量就认为是特征向量。

/[/mathbf{T}(/vec{/mathbf{v}}) = /underbrace{/mathbf{A}}_{n/times n}/vec{/mathbf{v}} = /underbrace{/lambda}_{特征值} /overbrace{/vec{/mathbf{v}}}^{特征向量}/]

其中， /(T/) 是一种线性变换，我们知道线性变换可以用矩阵向量积来表示，因此可以表示成 /mathbf{A}/vec{/mathbf{v}}。/(/mathbf{A}/) 是一个 /(n/times n/) 的方阵。/(/vec{/mathbf{v}}/) 就是特征向量（Eigen Vector），也就是 能被伸缩的向量 （要求是非 /(/mathbf{0}/) 向量），而 /(/lambda/) 是特征向量 /(/vec{/mathbf{v}}/) 所对应的特征值，也就是 伸缩了多少 。如果特征值是负数，那说明了矩阵不但把向量拉长（缩短）了，而且让向量指向了相反的方向。

听起来很抽象，放个例子就清楚了。下图出自 wikipedia的《 特征向量 》一文：

在这个仿射变换中，蒙娜丽莎的图像被变形，但是中心的纵轴在变换下保持不变。（注意：角落在右边的图像中被裁掉了。）蓝色的向量，从胸部到肩膀，其方向改变了，但是红色的向量，从胸部到下巴，其方向不变。因此红色向量是该变换的一个特征向量，而蓝色的不是。因为红色向量既没有被拉伸又没有被压缩，其特征值为1。所有沿着垂直线的向量也都是特征向量，它们的特征值相等。它们构成这个特征值的特征空间。

求解特征值

非 /(/mathbf{0}/) 向量 /(/vec{/mathbf{v}}/) 是线性变化矩阵 /(/mathbf{A}/) 的特征向量，需要满足如下条件

eq: 1 »

：

/[det(/lambda /mathbf{I}_n - /underbrace{/mathbf{A}}_{n/times n}) = 0/]

其中，/(det/) 表示矩阵行列式，/(/lambda/) 是特征值，/(/mathbf{I}/) 是单位矩阵。

例如矩阵 /(/mathbf{A} = /begin{bmatrix}1 & 2 // 4 & 3/end{bmatrix}/) ，代入公式 2 得：

/[ /begin{align} det/left( /lambda /begin{bmatrix} 1 & 0 // 0 & 1 /end{bmatrix}-/begin{bmatrix} 1 & 2 // 4 & 3 /end{bmatrix} /right) &=0 // det/left( /begin{bmatrix} /lambda & 0 // 0 & /lambda /end{bmatrix}-/begin{bmatrix} 1 & 2 // 4 & 3 /end{bmatrix} /right) &=0 // det/left( /begin{bmatrix} /lambda -1 & -2 // -4 & /lambda -3 /end{bmatrix} /right) &=0 /end{align} /]

所以有：

/[/begin{align} (/lambda -1)(/lambda -3)-8 & =0 // /lambda ^{ 2 }-4/lambda -5 &=0 // (/lambda - 5)(/lambda +1) &= 0/end{align}/]

因此 /(/lambda/) 的值为 5 或者 -1 。

在 Python 中，可以使用 numpy.linalg.eigvals 方法求解一个方阵的特征值：

>>> a = np.matrix('1 2;4 3')
>>> print np.linalg.eigvals(a)
[-1.  5.]

前面说了变换矩阵必须是方阵，所以如果用在其他形状的矩阵上就会抛出 LinAlgError 错误：

>>> b = np.matrix('1 2 3;4 3 1')
>>> print np.linalg.eigvals(b)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "/usr/local/lib/python2.7/dist-packages/numpy/linalg/linalg.py", line 902, in eigvals
    _assertNdSquareness(a)
  File "/usr/local/lib/python2.7/dist-packages/numpy/linalg/linalg.py", line 212, in _assertNdSquareness
    raise LinAlgError('Last 2 dimensions of the array must be square')
numpy.linalg.linalg.LinAlgError: Last 2 dimensions of the array must be square

求解特征向量

变换矩阵 /(/mathbf{A}/) 的特征空间（特征向量张成的空间）可以用下面的等式来求解：

eq: 2 »

/[/mathbf{E}_{/lambda}=N(/lambda I_n - /mathbf{A})/]

例如上面的变换矩阵 /(/mathbf{A} = /begin{bmatrix}1 & 2 // 4 & 3/end{bmatrix}/) ，代入公式 3 得：

/[{ E }_{ /lambda }=N/left( /lambda I_{ n }-/begin{bmatrix} 1 & 2 // 4 & 3 /end{bmatrix} /right) =N/left( /lambda /begin{bmatrix} 1 & 0 // 0 & 1 /end{bmatrix}-/begin{bmatrix} 1 & 2 // 4 & 3 /end{bmatrix} /right) =N/left( /begin{bmatrix} /lambda -1 & -2 // -4 & /lambda -3 /end{bmatrix} /right) /]

当 /(/lambda = 5/) 时，

/[{ E }_{ 5 }=N/left( /begin{bmatrix} 4 & -2 // -4 & 2 /end{bmatrix} /right) /]

利用前面所学的，得

/[{ E }_{ 5 }= span/left(/begin{bmatrix}/frac{1}{2} // 1 /end{bmatrix}/right) /]

同样地，当 /(/lambda = -1/) 时，

/[{ E }_{ -1 }= span/left(/begin{bmatrix}1 // -1 /end{bmatrix}/right) /]

在 Python 中，可以使用 numpy.linalg.eig 方法来求解方阵的特征值和特征向量：

>>> a = np.matrix('1 2;4 3')
>>> print np.linalg.eig(a)
(array([-1.,  5.]), matrix([[-0.70710678, -0.4472136 ],
        [ 0.70710678, -0.89442719]]))

得到的元组中，第一部分是特征值，和前面使用 numpy.linalg.eigvals 得到的结果完全一样；第二部分是特征向量，乍一看好像和我们上面求解的结果不一样，但如果我们这么写就完全一样了：/(/begin{bmatrix}-0.70710678/begin{bmatrix}1 // -1/end{bmatrix} & -0.89442719/begin{bmatrix}/frac{1}{2} // 1/end{bmatrix} /end{bmatrix}/)

小结

终于完成了线性代数的系列。作为保研党，真正系统学习线性代数也就是在大一的时期，然后大学四年也没怎么用到数学，渐渐地就忘得差不多了。后来读研的时候虽然也用到些线性代数，但都是用到啥补啥，跟其他考研上来的同学比起来，心里面总是缺少一点底气。在中科院实习结束的时候，陈宝权老师和 Andrei 一直劝我读博，最后我婉拒了，其中一个原因也和这个“没底气”有关吧。而今我也工作快两年了，虽然还是没有读博的念头，但还是希望把数学捡起来，让自己也有底气一些。

读者也许会发现最近我很喜欢写系列文章。我倒不是为了要出书啦。只是我觉得既然博客的文章不止是写给我一个人看的，那么也得考虑读者的感受。如果把一篇文章写得太长，那就很难让人坚持读完，更别说这种公式很多的文章了；而如果写得太短，又不够完整，读得不够尽兴，于我也没有多少益处。

写系列文章其实最大的难点在于把握好 tradeoff 。像线性代数的知识点，两三篇文章的篇幅肯定是讲不完的，有些知识点如果再深入一下，就又拔出萝卜带出泥。比如最后一节提到特征向量，其实我还可以继续讨论特征值分解，然后又可以扯到奇异值分解。这样就很容易把整个系列写成像裹脚布一样了。所以，我只讲最基础的知识点，而且是可能对机器学习有帮助的，目的是让自己今后读相关的文章时有底气一些，至少不会在“秩”、“转置矩阵”这种最基础的知识点上犯晕。有了这个基础后，再去学习像奇异值分解之类的其他知识也会轻松很多。如果这个系列也能对读者们有所帮助，那就再好不过了。

如果您希望将这个线性代数子系列保存为书签，作为后面的工具文来查阅，我建议您保存我在wiki上的线性代数笔记（跳转入口）。因为我的 wiki 的更新频率会更频繁一些。且日后随着我的学习还可能继续添加一些新的内容。

下篇文章我将继续从一个机器学习工程师的角度，开始回顾微积分的基础知识点。