看穿机器学习（W-GAN模型）的黑箱
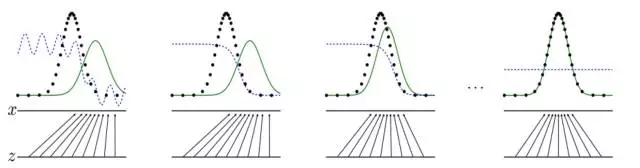
图a. Principle of GAN.
前两天纽约暴雪，天地一片苍茫。今天元宵节，长岛依然清冷寂寥，正月十五闹花灯的喧嚣热闹已成为悠远的回忆。这学期，老顾在讲授一门研究生水平的数字几何课程，目前讲到了2016年和丘成桐先生、罗锋教授共同完成的一个几何定理【3】，这个工作给出了经典亚历山大定理（Alexandrov Theorem）的构造性证明，也给出了最优传输理论（Optimal Mass Transportation）的一个几何解释。这几天，机器学习领域的Wasserstein GAN突然变得火热，其中关键的概念可以完全用我们的理论来给出几何解释，这允许我们在一定程度上亲眼“看穿”传统机器学习中的“黑箱”。下面是老顾下周一授课的讲稿。
生成对抗网络 GAN
训练模型 生成对抗网络GAN （Generative Adversarial Networks）是一个“自相矛盾”的系统，就是以己之矛克以己之盾，在矛盾中发展，使得矛更加锋利，盾更加强韧。这里的矛被称为是判别器（Descriminator），这里的盾被称为是生成器（Generator）。
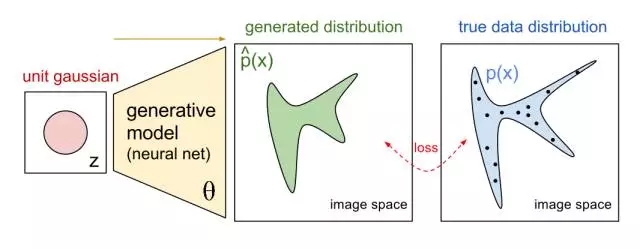
图b. Generative Model.
生成器G一般是将一个随机变量（例如高斯分布，或者均匀分布），通过参数化的概率生成模型（通常是用一个深度神经网来进行参数化），进行概率分布的逆变换采样，从而得到一个生成的概率分布。判别器D也通常采用深度卷积神经网。
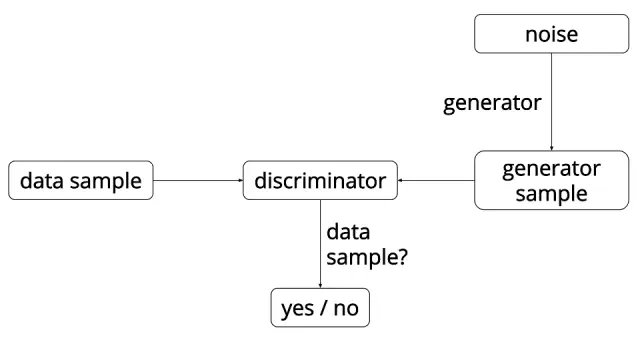
图1. GAN的算法流程图。
在训练中，判别器D和生成器G交替学习，最终达到纳什均衡（零和游戏），判别器无法区分真实样本和生成样本。
优点 GAN具有非常重要的优越性。当真实数据的概率分布不可计算的时候，传统依赖于数据内在解释的生成模型无法直接应用。但是GAN依然可以使用，这是因为GAN引入了内部对抗的训练机制，能够逼近一下难以计算的概率分布。更为重要的，Yann LeCun一直积极倡导GAN，因为GAN为无监督学习提供了一个强有力的算法框架，而无监督学习被广泛认为是通往人工智能重要的一环。
为此，我们引入最优传输的几何理论（Optimal Mass Transportation），这个理论可视化了W-GAN的关键概念，例如概率分布，概率生成模型（生成器），Wasserstein距离。更为重要的，这套理论中，所有的概念，原理都是透明的。例如，对于概率生成模型，理论上我们可以用最优传输的框架取代深度神经网络来构造生成器，从而使得黑箱透明。
最优传输理论梗概
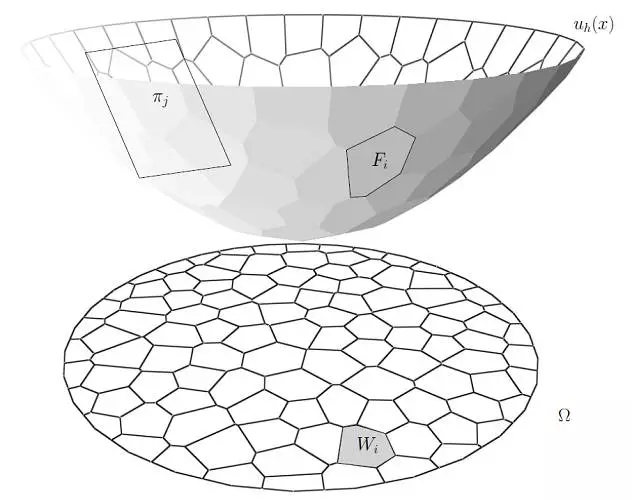
图2. 亚历山大定理。
后面，我们可以看到，这个凸多面体就是Brenier势能函数，其梯度映射将一个概率分布.映到另外一个概率分布，并且这两个概率分布之间的Wasserstein 距离对偶于此凸多面体决定的体积。理论上，这个凸多面体可以作为W-GAN模型中的生成器G。
W-GAN中关键概念可视化
Wasserstein-GAN模型中，关键的概念包括概率分布（概率测度），概率测度间的最优传输映射（生成器），概率测度间的Wasserstein距离。下面，我们详细解释每个概念所对应的构造方法，和相应的几何意义。
图3. 由保角变换（conformal mapping）诱导的圆盘上概率测度。
概率测度可以看成是一种推广的面积（或者体积）。我们可以用几何变换随意构造一个概率测度。如图3所示，我们用三维扫描仪获取一张人脸曲面，那么人脸曲面上的面积就是一个概率测度。我们缩放变换人脸曲面，使得总曲面等于π。然后，我们用保角变换将人脸曲面映射到平面圆盘。如图3所示，保角变换将人脸曲面上的无穷小圆映到平面上的无穷小圆，但是，小圆的面积发生了变化。每对小圆的面积比率定义了平面圆盘上的概率密度函数。
图4. 两个概率测度之间的最优传输映射。
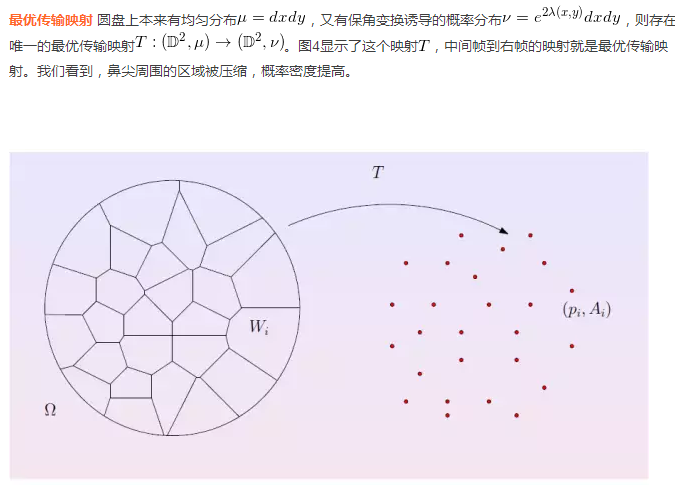
图5. 离散最优传输。
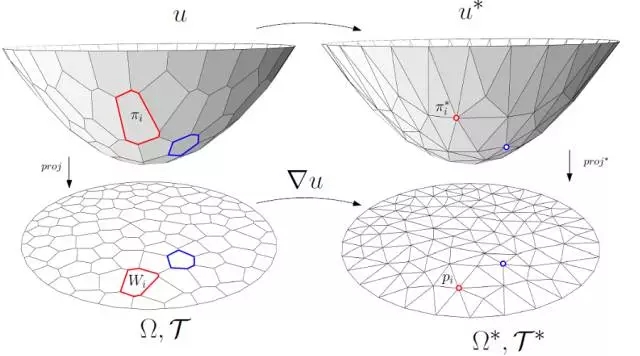
图6. 离散Brenier势能函数，离散最优传输映射。
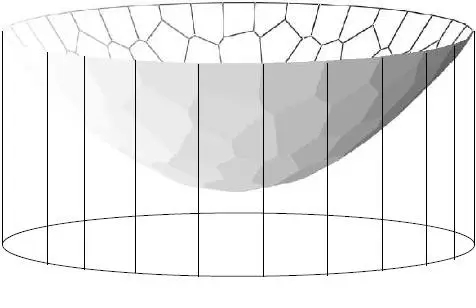
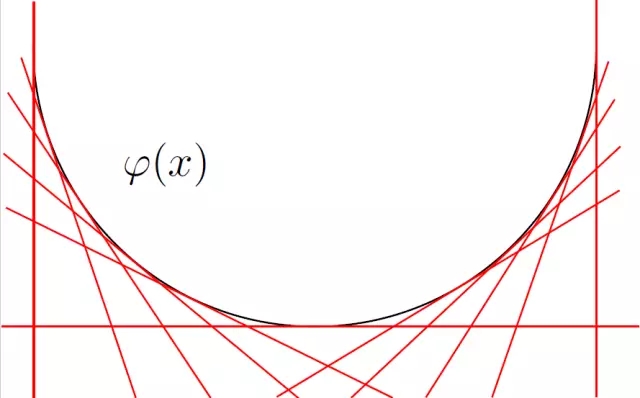
图8.凸函数的图像由其切线包络而成，切线集合被表示成原函数的勒让德对偶。
图9. 图解勒让德变换。
总结
通过以上讨论，我们看到给定两个概率分布 
，则存在唯一的一个凸函数（Brenier 势函数） 
，其梯度映射 
把一个概率分布T映成了另外一个概率分布。这个最优传输映射的传输代价就给出了两个概率分布之间的Wasserstein距离。Brenier势能函数，Wasserstein距离都有明晰的几何解释。
在Wasserstein-GAN模型中，通常生成器和判别器是用深度神经网络来实现的。根据最优传输理论，我们可以用Briener势函数来代替深度神经网络这个黑箱，从而使得整个系统变得透明。在另一层面上，深度神经网络本质上是在训练概率分布间的传输映射，因此有可能隐含地在学习最优传输映射，或者等价地Brenier势能函数。对这些问题的深入了解，将有助于我们看穿黑箱。
图10. 基于二维最优传输映射计算的曲面保面积参数化（area preserving parameterization），苏政宇作。
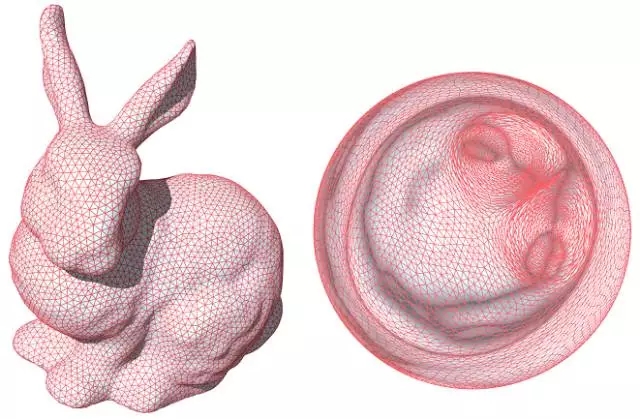
图11. 基于三维最优传输映射计算的保体积参数化 （volume preserving parameterization），苏科华作。
（在2016年，老顾撰写了多篇有关最优传输映射的博文，非常欣慰地看到这些文章启发了一些有心的学者，发表了SIGGRAPH论文，申请了NSF基金。感谢大家关注老顾谈几何，希望继续给大家灵感。）
参考资料
[1]Arjovsky, M. & Bottou, L.eon (2017) Towards Principled Methods for Training Generative Adversarial Networks
[2] Arjovsky, M., Soumith, C. & Bottou, L.eon (2017) Wasserstein GAN.
[3] Xianfeng Gu, Feng Luo, Jian Sun and Shing-Tung Yau, Variational Principles forMinkowski Type Problems, Discrete Optimal Transport, and Discrete Monge-Ampere
Equations, Vol. 20, No. 2, pp. 383-398, Asian Journal of Mathematics (AJM), April 2016.
欢迎加入本站公开兴趣群
商业智能与数据分析群
兴趣范围包括各种让数据产生价值的办法，实际应用案例分享与讨论，分析工具，ETL工具，数据仓库，数据挖掘工具，报表系统等全方位知识
QQ群：81035754
正文到此结束
热门推荐
相关文章
近期评论
-
666
-
文章和留言都翻到11页了 没有OOM
-
-
朋友，翻页到11页，及以后，会出现OOM，无法访问
-
-
-
-
版本号是多少，你可以下载哪个代码仓库，jdk选1.8 直接跑就行
-
-
Loading...
![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)
