转载

谷歌新论文提出批再规范化：可降低批规范化模型中的minibatch依赖

摘要：批规范化（Batch Normalization）可以十分有效地加速和提升深度模型的训练。但是，当训练的 minibatch 较小或不是由独立的样本组成时，它的有效性会降低。我们假设这是由 minibatch 中所有样本上的模型层输入（model layer inputs）的依赖性（dependence）和训练与推理之间产生的不同激活（activation）所造成的。我们提出了一种简单却有效的扩展——批再规范化（Batch Renormalization），以确保训练和推理模型可以基于单个样本而非整个 minibatch 而生成同样的输出。当用小或 non-i.i.d.（非独立同分布）minibatch 训练时，用批再规范化训练的模型的表现显著优于批规范化训练的模型。与此同时，批再规范化还保留了批规范化的优点，例如对初始化不敏感和训练效率。

算法 1：使用批再规范化的训练（上）和推理（下），其在一个 minibatch 上应用了激活 x。在反向传播过程中使用了标准的链式法则。用 stop_gradient 标记的值被当作一个给定训练步骤的常量处理，而且该梯度不会经由它们传播。

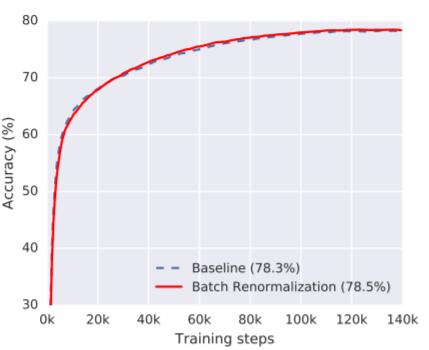
谷歌新论文提出批再规范化：可降低批规范化模型中的minibatch依赖

图 1：分别使用批规范化和批再规范化的 Inception-v3 模型的验证 top-1 准确度（validation top-1 accuracy），模型是在 50 个同步的工作器（worker）上训练的，其中每一个工作器处理大小为 32 的 minibatch。使用批再规范化的模型实现了略高一点的验证准确度。

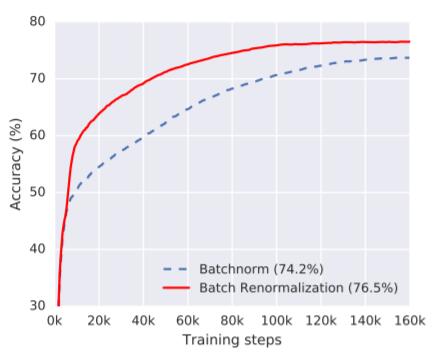
谷歌新论文提出批再规范化：可降低批规范化模型中的minibatch依赖

图 2：分别使用批规范化和批再规范化的模型的验证准确度，其中规范化是在有 4 个样本的集合上执行的（但带有被 50 个工作器处理过的在所有 50×32 个样本上聚集的梯度）。批再规范化让模型能更快地训练和实现更高的准确度，尽管规范化 32 个样本的集合会表现更好。

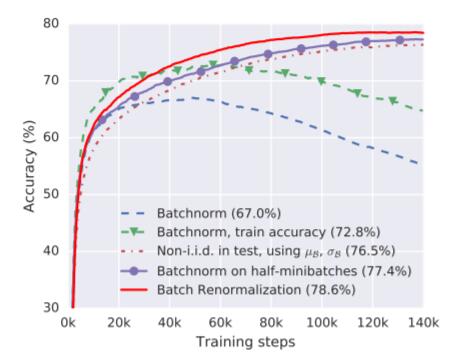
谷歌新论文提出批再规范化：可降低批规范化模型中的minibatch依赖

图 3：当在 non-i.i.d. minibatch 上训练时所得到的验证准确度，这是通过为 16 个（取自共 1000 个）随机标签中的每一个标签采样 2 张图像得到的。这种分布偏差不仅会导致测试的低准确度，也会导致在训练集上的低准确度，最后还会下降。这表明在这个特定的 minibatch 分布上出现了过拟合，这通过我们的改进得到了证实——当测试 minibatch 也是每个标签包含 2 张图像，并且批规范化在推理过程中使用了 minibatch 统计 µB、σB 时。如果批规范化被分别应用于一个训练 minibatch 的两半，使其中每一半都更 i.i.d.，那么它还会进一步提升。最后，通过使用批再规范化，我们可以仅通过正常的训练和评估就实现如我们在图 1 中的 i.i.d. minibatch 上所得到的同样的验证准确度。

原文 http://www.jiqizhixin.com/article/2276

正文到此结束