转载

Wasserstein GAN 的 TensorFlow 实现

Facebook 人工智能研究中心（FAIR）近日提出的 Wasserstein GAN 引起了人工智能研究界的广泛关注，参见机器之心的文章 《学界 | FAIR 提出常见 GAN 训练方法的替代方法：WGAN》和《专栏 | 看穿机器学习（W-GAN 模型）的黑箱》，其中在前一篇文章也给出了 WGAN 的 PyTorch 实现，今天这里要介绍的是 WGAN 的 TensorFlow 实现：WassersteinGAN.tensorflow。

项目地址：https://github.com/shekkizh/WassersteinGAN.tensorflow

相关链接：

论文地址：https://arxiv.org/abs/1701.07875
PyTorch 实现：https://github.com/martinarjovsky/WassersteinGAN
Reddit 上有趣的讨论：https://www.reddit.com/r/MachineLearning/comments/5qxoaz/r_170107875_wasserstein_gan/

注意：该实现引用的论文将鉴别器（discriminator）写作 critic，以下叙述中两个词会交替出现。

最近，一篇引人关注的论文讨论了 GAN 的稳定性和训练中损失函数的可解释性。GAN 本质上是一种试图通过生成对抗数据，通过最小化 f-divergence（概率分布的差异）来学习真实数据分布的模型。最初提出的 GAN 的最小最大目标的收敛可以解释为最小化 Jensen Shannon（JS）散度（divergence）。在本论文的研究中，作者发现当被比较的两个分布的支撑集不重叠时，这种方式存在缺陷，并提出了使用 earth movers/wasserstein distance 作为 JS 的替代品。同样在 f-divergence metrices 上的例子进一步支持了这一观点。注意，当 f-divergence 是离散的（如在 JS 和 KL 中），我们可能在具有梯度的学习模型中遇到问题，因为散度损失并不是在每一处都是可微分的。

该论文中提出的定理 1 是大多数人认为 wasserstein distance 能够帮助训练 GAN 的关键。该定理阐述了相对于其参数和局部 lipchitz 是连续的分布映射函数（critic）具有连续的和几乎无处不在的可微分 wasserstein distance。

连续性和几乎无处不在的微分度量将意味着我们可以在对生成器进行更新之前大强度地训练鉴别器，前者进而将接收改进的可靠梯度以从鉴别器进行训练。由于训练鉴别器强烈地导致消失的梯度，使用早期的 GAN 的方式不可能进行这样的训练。

鉴于神经网络在参数方面通常是连续的，所以可以确定的是 critic 是 Lipschitz 的。通过在 critic 中剪裁权重参数，我们可以在模型接近线性增长时阻止它饱和。这意味着函数的梯度由该线性度的斜率成为了 Lipschitz 界限的边界。

先决条件

该代码在使用英伟达 Titan GPU 的 Linux 系统中经过了测试
模型在 TensorFlow v0.11 与 Python2.7 的环境下经过了训练。新版本的 TensorFlow 需要更新 summary statements 以防止错误警告
请手动下载和解压 CelebA 数据集，下载链接：https://www.dropbox.com/sh/8oqt9vytwxb3s4r/AADIKlz8PR9zr6Y20qbkunrba/Img/img_align_celeba.zip
main.py 的默认 arguments 运行带有交叉熵目标函数的 GAN
run_main.sh 有运行 Wasserstein GAN 模型的命令

结果

用于训练模型的网络架构与原始 DCGAN 中使用的网络架构非常相似。这不同于在论文研究中 PyTorch 版本代码中所实现的生成器和鉴别器都有「额外层（extra layers）」跨度的结果。
网络中的所有偏差项都已被去除。我们目前还无法确定在生成器中丢弃偏差的理由，但在 critic 中，我们可能必须将函数约束到更小的 lipschitz 边界内。
以下结果是在 1e5 次迭代后，我们的系统花了大约 18 小时得到的。这可能不是最收敛的结果，所以不要对此过于严肃。

在训练 GAN 之后生成的图像的随机样本的 wasserstein distance 为 1e5 次迭代，lr = 5e-5，RMSPropOptimizer。

Wasserstein GAN 的 TensorFlow 实现

作为比较：使用具有交叉熵目标的GAN生成的图像的随机采样为2e4 次迭代，lr = 2e-4，AdamOptimizer。

Wasserstein GAN 的 TensorFlow 实现

观察报告

在经过长时间的试验后，我们发现实现论文中的理论是如此的简单。从实现的角度来看，主要的变化是：

鉴别器/critic 不再产生 S 形或概率输出。鉴别器的损失是简单的实际和生成图像之间的输出差。
每一次升级生成器后都要多次训练 critic。
Critic 的权重被限制在接近零的低值上。
需要不使用动量的低学习率和优化器。
在给定了非常低的学习率和在每次生成器升级后，鉴别器多次升级的情形下，训练的速度会非常慢，这是我们事先料到的。

Wasserstein GAN 鉴别器损失。注意在原论文中鉴别器损失被标记了负号，因此在图上的方向出现了翻转。据我观察，鉴别器的总体趋势是收敛的，但它在特定区间可能会有一些涨落。

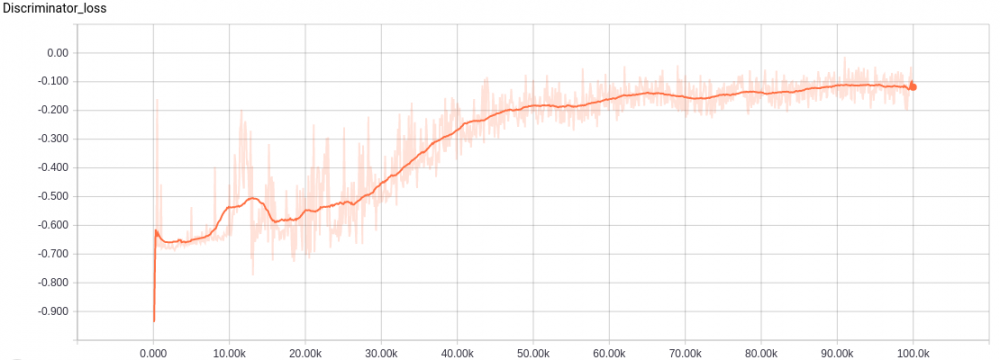
Wasserstein GAN 的 TensorFlow 实现

在这个问题空间中最小化 wasserstein distance 的训练可以解释为使得 critic 将低值分配给真实数据，将高值分配给假数据。另一方面，生成器试图生成 critic 给予的类似真实图像那样的低值图像。换句话说，当 critic 不再能够区分和分配不同的值到生成的和真实的图像时，模型收敛——所以我认为论文中把鉴别器（discriminator）称作是 critic 有一些道理。
上文提到的生成器试图为 critic 分配像真实图像那样的低值。虽然训练生成器得到的值一直接近于零。

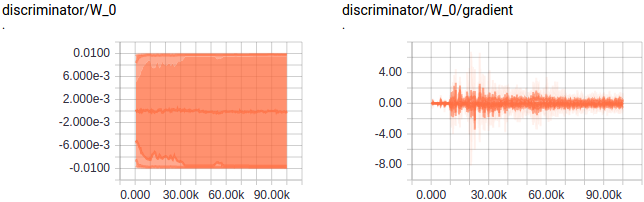
Wasserstein GAN 的 TensorFlow 实现