转载

【机器学习】tensorflow: GPU求解带核函数的SVM二分类支持向量机

SVM本身是一个最优化问题，因此理所当然可以用简单的最优化方法来求解，比如SGD。2007年pegasos就发表了一篇文章讲述简单的求解SVM最优化的问题。其求解形式简单，但是并没有解决核函数计算量巨大的问题。这里给出了一个tensorflow的带核函数的SVM的解法，使用GPU加速，并且支持在线学习。
pegasos给出的优化公式如下：

a r m i n λ 2 ∑ i , j α i α j ( x i , x j ) + ∑ i m a x { 0 , 1 − i ∑ j α j ( x i , x j ) } p r e i c t : = ∑ α i i ( x , x i )

我用rbf核函数来试验一下。其中数据以半径为10的圆圈分割成两个部分。tensorflow代码如下：

sigma = 0.5
kkx = np.square(np.tile(x[:,0].T,[x.shape[0],1])-np.tile(x[:,0],[1,x.shape[0]]))
#print(kkx)
kkx += np.square(np.tile(x[:,1].T,[x.shape[0],1])-np.tile(x[:,1],[1,x.shape[0]]))
kkx = np.sqrt(kkx)
kkx = np.exp(-sigma * kkx )
lam = 1./2.
batch = x.shape[0]
with tf.device('/gpu:0'):#使用GPU计算
    alpha = tf.Variable(tf.random_uniform([batch,1],-1.0,1.0))
    alpha = tf.maximum(0.,alpha)
    KX = tf.placeholder("float", shape=[batch,batch])
    y = tf.placeholder("float", shape=[batch,1])
    loss = lam*tf.reduce_sum(tf.matmul(alpha,tf.transpose(alpha))*KX)
    tmp = tf.matmul(KX, alpha)
    tmp = y*tmp
    tmp = 1. - tmp
    tmp = tf.maximum(0.,tmp)
    tmp = 1./batch*tf.reduce_sum(tmp)
    loss += tmp
    optimizer = tf.train.GradientDescentOptimizer(0.0002)
    train_op = optimizer.minimize(loss)

为了简化，KX直接用numpy计算好 ( x i , x j )

$K(x_i,x_j)$ 之后传入。经过优化后，我们取出 α $/alpha$ ，这里我不去掉0，就直接套用在原来的数据上进行预测：

resA = sess.run(alpha)
predict=np.multiply(resA,x[:,2])
#print(predict.shape)
predict=np.sum(np.multiply(predict,kkx),axis=0)
predict = predict.T
predict=np.tile(predict,[1,3])
#print(predict>0.0)
ax = np.array(x)
predictSet1=ax[predict>0.0].reshape([-1,3])
predictSet2=ax[predict<0.0].reshape([-1,3])
fig = plt.figure()
ax = fig.add_subplot(211)
ax.scatter(x=data1[:,0],y=data1[:,1])
ax.scatter(x=data2[:,0],y=data2[:,1])
ax = fig.add_subplot(212)
ax.scatter(x=predictSet1[:,0],y=predictSet1[:,1])
ax.scatter(x=predictSet2[:,0],y=predictSet2[:,1])
fig.show()

得到图像如下：
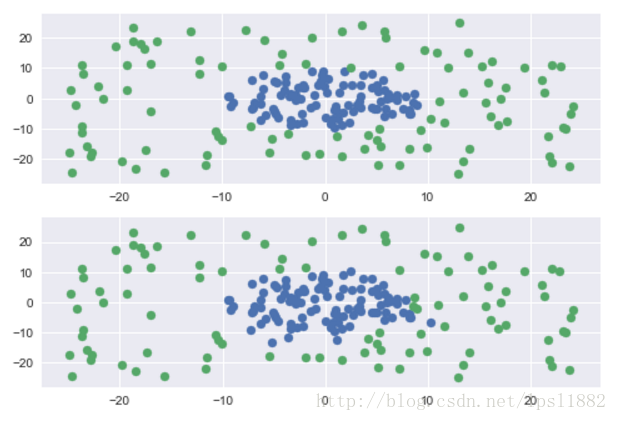
【机器学习】tensorflow: GPU求解带核函数的SVM二分类支持向量机
上图是原始数据集，下图是预测集。可以看出来，tensorflow能够优化求解svm，比较万金油。