卷积神经网络可视化:以Keras处理猫图片为例
众所周知,在过去几年里,深度学习领域里的很多主要突破都来源于卷积神经网络(CNNs 或者 ConvNets),但对大多数人来说卷积神经网络是一个非常不直观的推断过程。我一直想剖析卷积神经网络的各个部分,看看它在每个阶段的图像处理结果是怎样的,而本篇文章就是我的方法简述。
从高层来看卷积神经网络
首先,卷积神经网络擅长干什么?卷积神经网络主要被用来寻找图像中的特征。你可以通过卷积一幅图像来寻找这些特征。卷积神经网络的前几层能够识别线和角,而后随着我们把神经网络做得更深(层更多),我们能把这些特征在神经网络里继续传递下去,并在神经网络的高层开始识别更复杂的特征。卷积神经网络的这个特性使得它非常擅长图像中的物体识别。
什么是卷积神经网络?
卷积神经网络是一个通常包含几种不同类型层的神经网络,它里面每一层是卷积层、或者池化(Pooling)层、或者激活层,三者之一。
卷积层
为了理解卷积神经网络是什么,你需要理解卷积是如何工作的。想象一下,你有一个由 5x5 的矩阵数组表示的图像,而你有一个 3x3 大小的矩阵,沿着图像滑动这个 3x3 的矩形窗。在 3x3 窗所访问的每个位置,会把当前窗口所覆盖的图像像素值与 3x3 矩形窗中的值进行矩阵乘。这个矩阵乘得到了一个数值,它用来代表图像中那个窗口覆盖下的所有值。为了明晰这个过程,这里有一个非常好的 gif 图:

正如你所看到的,特征矩阵中的每一项对应图像中的一个区域。(注意:核矩阵的值是 gif 图角落里的红色数字。)
那个「访问」完整张图像的「窗口」被称为核(kernel)。核通常是正方形的,而且对于小型图像来说,3x3 是一个相当常见的核尺寸。窗口每次滑动的距离被称为步长(stride)。需要额外说明的是,在做卷积时有时需要在图像的边界外附上一圈零值,用来抑制图像边缘的卷积值(其基本想法是一般情况下的图像中间部分更为重要)。
卷积层的目的是用来滤波。当我们遍历图像时,我们能有效的查看相应图像区域的特征。之所以能做到这一点是因为滤波器,以及许多组成向量的权重值,这些权重值是由卷积的输出结果相乘而来的。当训练一幅图像时,这些权重值会发生变化,所以当到了真实场景中去评估一幅图像时,如果神经网络认为它「看」到了一个以前「看」到过的特征,那么这些权重将会被赋予高值。从各种滤波器得到的这些高权值的组合会使网络能够预测图像的内容。这就是为什么在卷积神经网络结构图中,卷积这步是用一个盒子表示的而不是一个矩形;第三维代表的是滤波器。
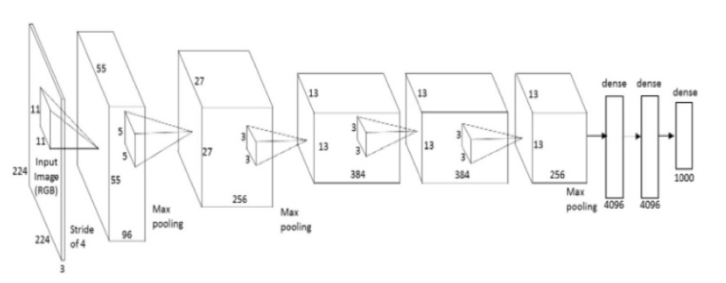
AlexNet 的架构
需要注意:
-
卷积的输出(长和宽)小于原始图像
-
核与核下面的图像窗口之间做的是一种线性函数运算
-
滤波器的权值可以通过「看」很多图像来学习得到
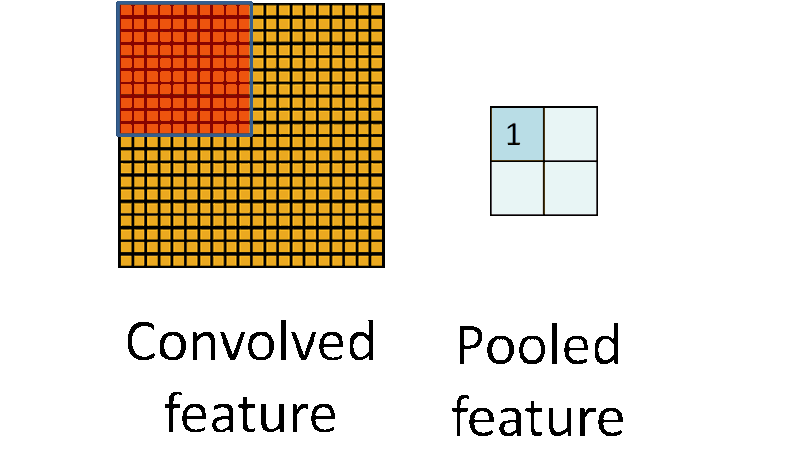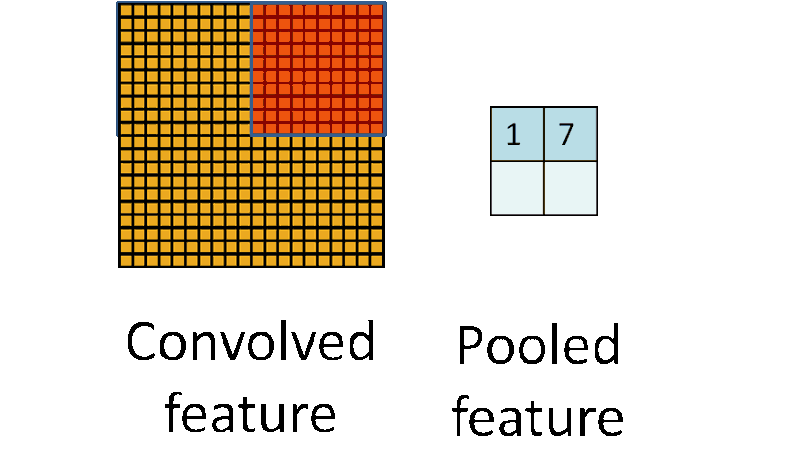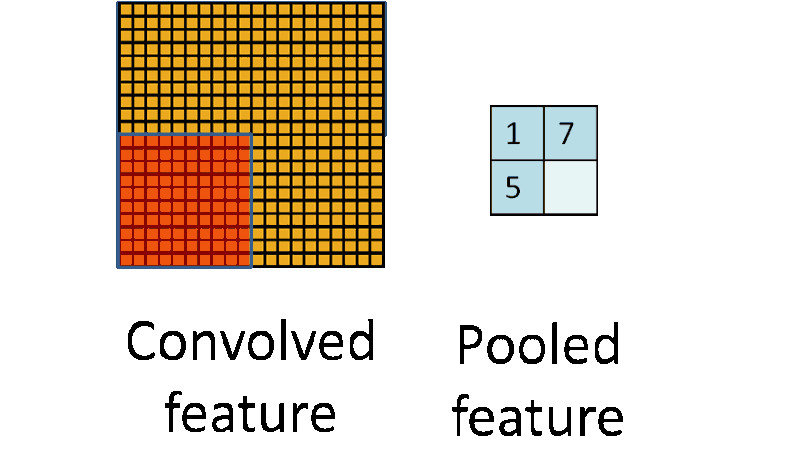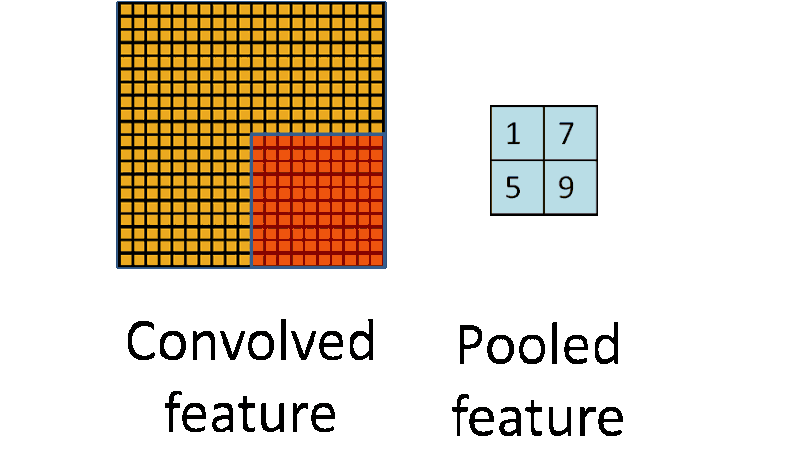
池化(pooling)层
池化的操作很像卷积,它们都是采用一个核来遍历整个图像,唯一的不同是用于计算核和图像窗口值的函数不是线性的。
最大池化和平均池化是两种最常用的池化函数。最大池化取当前核覆盖窗口下的图像最大值,而平均池化取核覆盖窗口下对应所有图像值的平均值。
激活层
卷积神经网络中激活层的工作方式与激活层在其他神经网络中的工作过程是完全一致的,即一个值通过函数处理后都被「压缩」到一个特定范围内。这里是一些常用的激活函数:
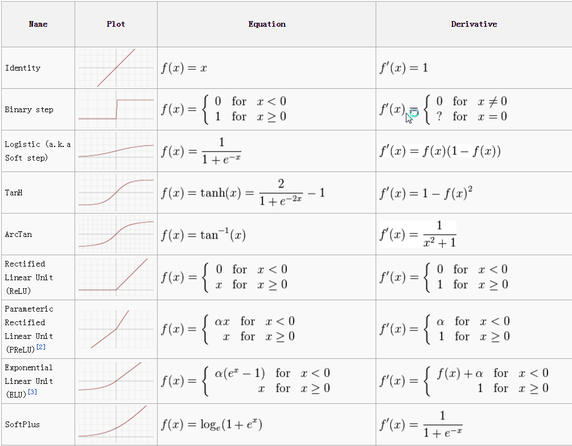
在卷积神经网络中最常用的激活函数是 ReLU(修正线性单元)。人们喜欢用 ReLU 出于很多种原因,其中最大原因是因为执行起来开销很小,如果当前的数为负:输出值 0;其他情况:输出值为这个数本身。开销低使得它能更快的训练网络。
扼要重述
-
卷积神经网络三种主要层的类型:卷积(Convolutional)、池化(Pooling)、激活(Activation)
-
卷积层将图像窗口与核值相乘,随着时间的推移使用梯度下降来优化核权重
-
池化层使用图像在核窗口下的最大值或平均值来描述该图像的窗口
-
激活层将核值限定在某个范围内,通常范围是 [0,1] 或 [-1,1]
卷积神经网络看起来是什么样的?
在我们进入主题之前,先来了解一些相关背景。第一个成功的 CNN 应用由 Yann LeCun 于 90 年代实现,他创造了一种叫做 LeNet 的网络,可用于阅读手写数字。从那时起,计算方面的进展以及 GPU 的强大性能助长了研究人员的雄心壮志。2010 年,斯坦福视觉实验室(Stanford Vision Lab)发布了 ImageNet 数据集——包含有 1400 万张带有详细信息标签的图像。这个数据集已成为研究领域中用于比较 CNN 模型的标准之一,而当前世界上最好的模型可以成功检测数据集中 94% 以上的图像。时不时的经常有新模型出现并在检测结果上打败以往的高分模型而且这是一件很了不起的事。2014 年是 GoogLeNet 和 VGGNet,在这之前是 ZF Net。应用于 ImageNet 的第一个切实可行 的 CNN 实例是 2012 年的 AlexNet,在此之前,研究人员尝试在 ImageNet 上使用传统的计算机视觉技术,AlexNet 的表现优于之前所有出现过的技术大约 15 个百分点。
不管怎么说,来看看 LeNet 的结构:
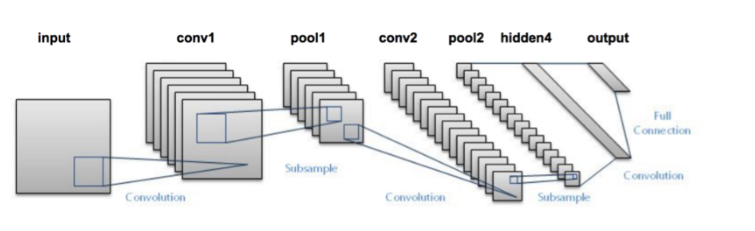
LeNet 架构
这张图表并没有显示激活函数,不过整体架构是这样的:
输入图片→卷积层→激活函数(ReLU)→最大池化(MaxPooling)→卷积层→激活函数(ReLU)→最大池化→隐藏层→Softmax(激活)→输出层
识别猫的时候到了!
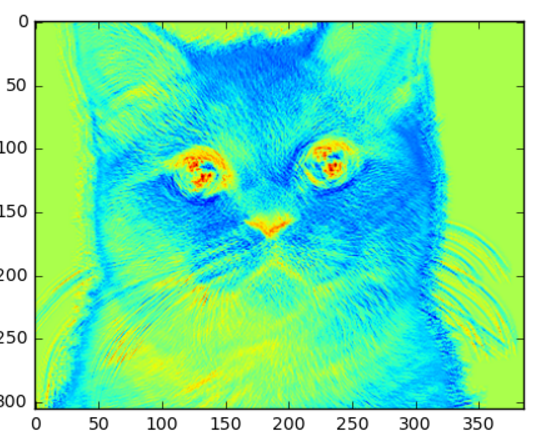
这是一张猫的图片:
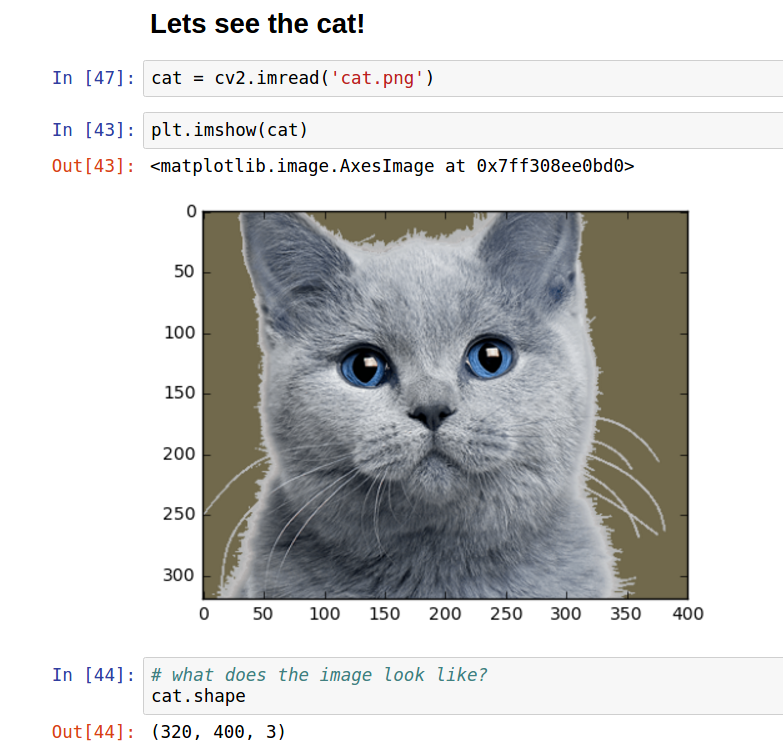
我们这张猫咪图片有 320 像素高、400 像素宽,RGB 三色通道模式
卷积层
那么它在经过一层卷积后看起来是什么样的?
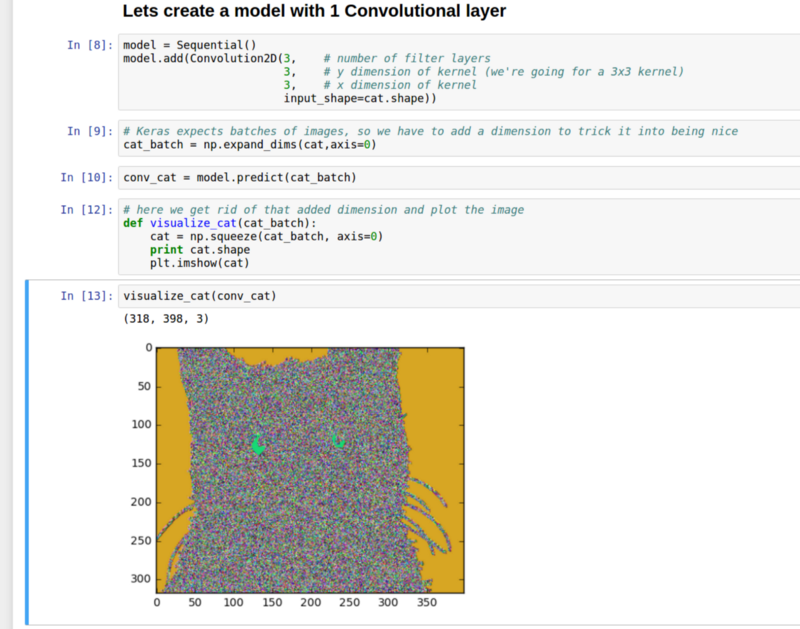 经过一次卷积之后猫的图片
经过一次卷积之后猫的图片
遍历这张猫图片的核尺寸为 3x3,有 3 个过滤器(如果超过 3 个过滤器则我们就不能绘制猫咪的 2D 图像。高维度的猫咪处理起来异常棘手。)。
这张猫咪图像看起来非常嘈杂,因为所有权重都是随机初始化的,而且我们还没有训练网络。再者它们彼此向上堆叠,因此即使每一层包含有详细信息我们也无法看到。不过我们可以找出图像中与猫眼睛颜色相同的区域以及背景颜色相同的区域。如果我们将核增大至 10x10 会发生什么?
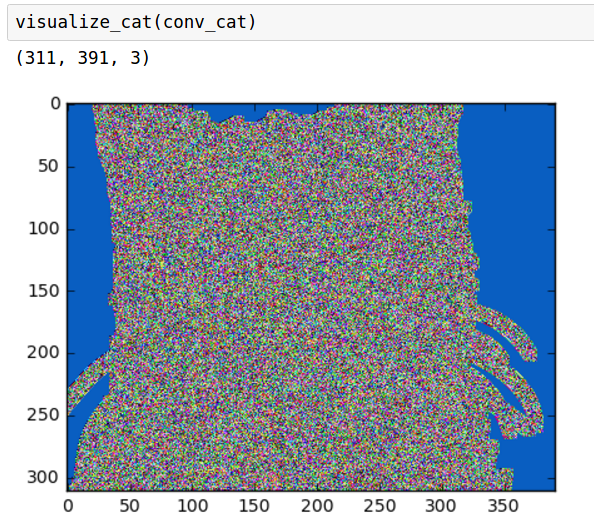
从上图可以看出,由于核过大,我们失去了一些细节。我们还注意到,图像形状由于更大的核而变得稍小,而这些东西是由数学计算所控制。
如果我们把它缩小一点,颜色通道会看起来好点吗?
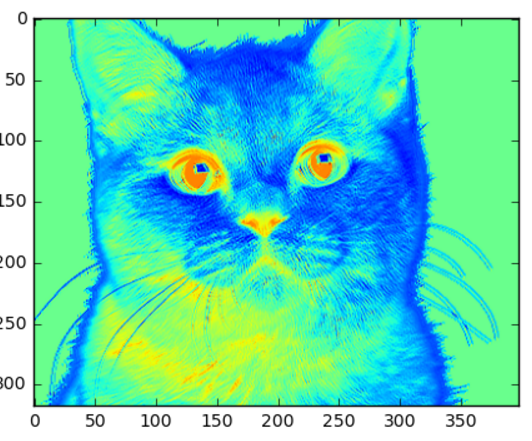
好多了!现在我们可以看到一些滤波器所「看到」的东西。看起来红色似乎真的很喜欢那一点黑色的鼻子和眼睛,而蓝色是在挖掘勾勒猫咪外形的浅灰色部分。我们可以开始看到层是如何捕捉照片中一些更重要细节的。
3x3 核的卷积猫

原图
15x15 像素的核
现在如果我们显著增大核尺寸,我们得到的图像细节就更少,而图像尺寸也比其他两幅更小了。
添加一个激活层
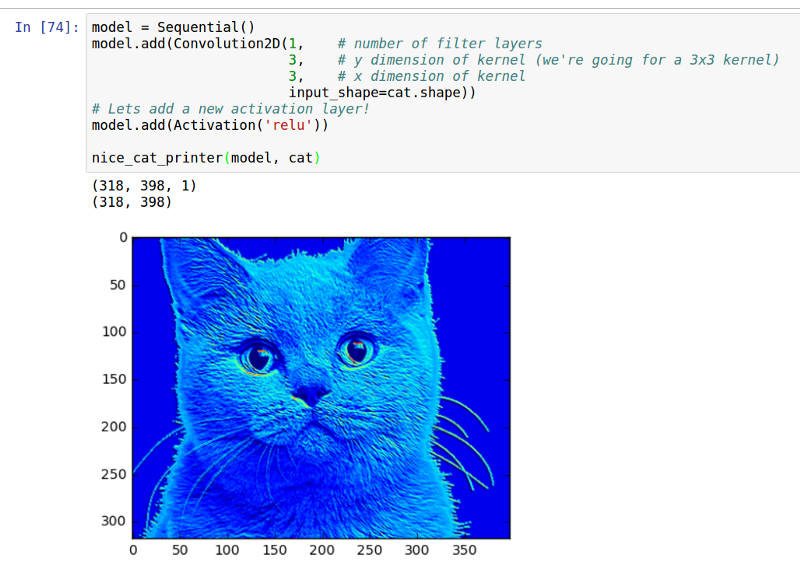
经过 ReLU 函数之后猫的图片
We get rid of a lot of the not blue-ness by adding a relu.
通过添加 ReLU 激活函数,我们去掉了许多非蓝色区。
添加一个池化层
我们添加了一个池化层(用最大池化是为了更易于显示出池化后的图片效果并去掉上一步的激活函数 ReLU)
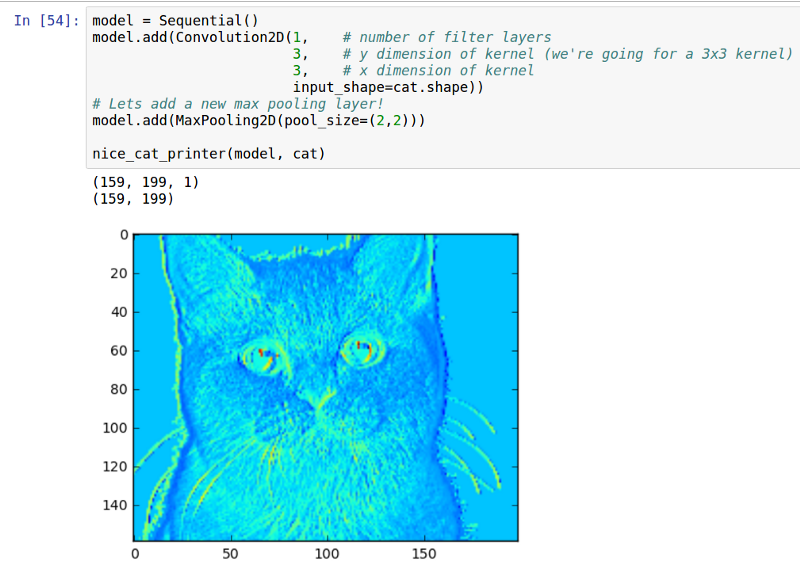
池大小 2x2
如所期望的那样,猫图片色块化了,不过我们还能做出更色块化的图片!
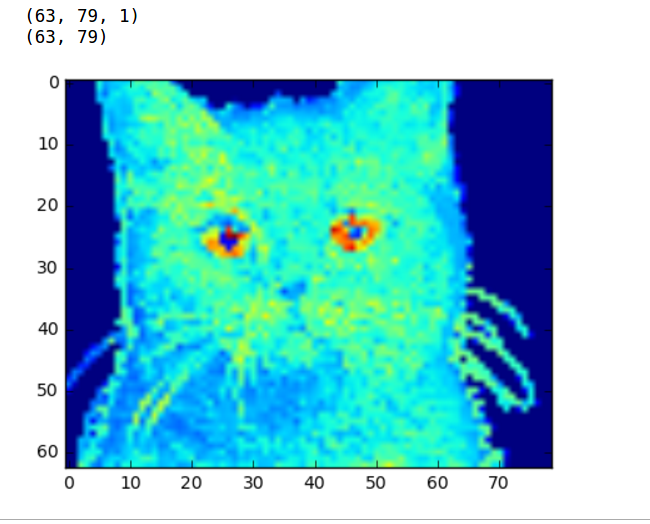
池大小 5x5 的猫池化图片。你的所有池化都属于我们
注意现在的图像大小是如何变成原始大小的三分之一的。
激活(Activation)与最大池化(MaxPooling)
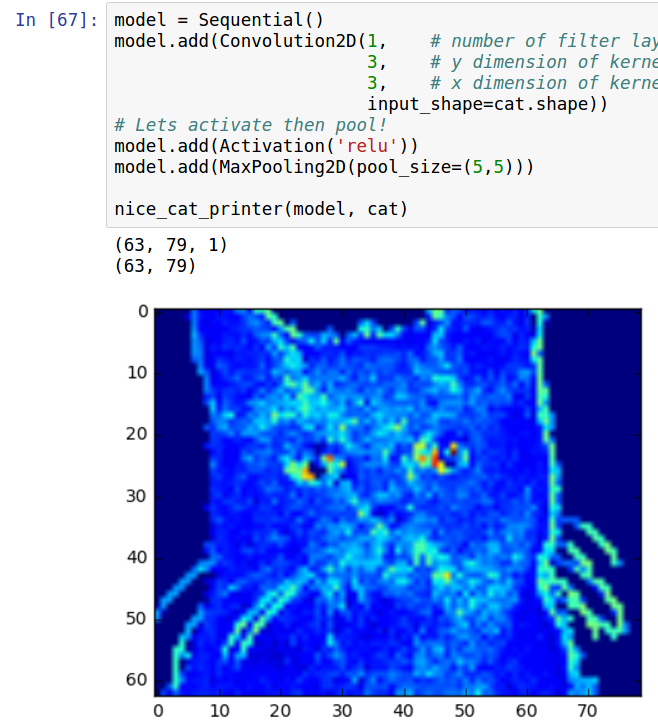
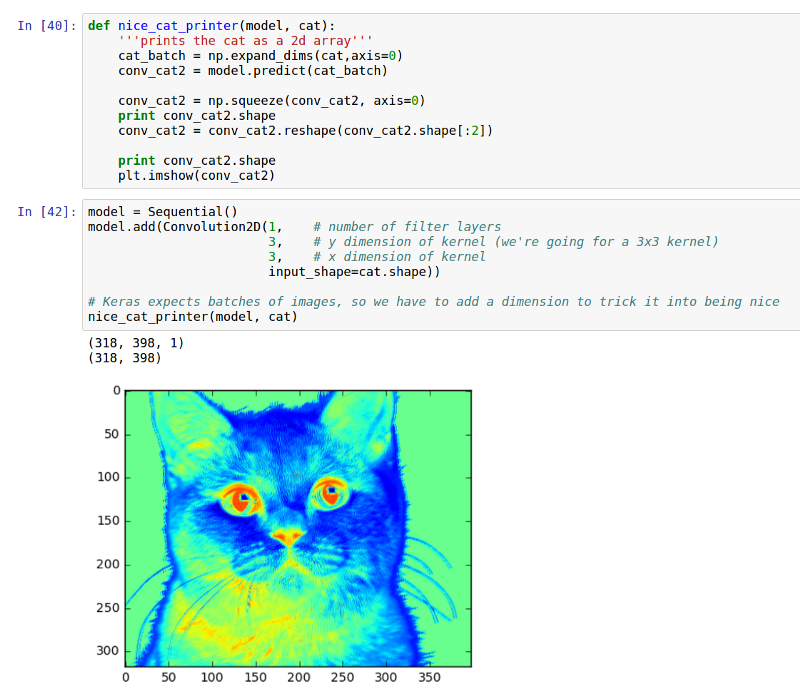
LeNet 模型处理的猫图片
如果我们将猫图片经由 LeNet 中卷积与池化部分处理,处理后的猫图片看起来会是怎样的?
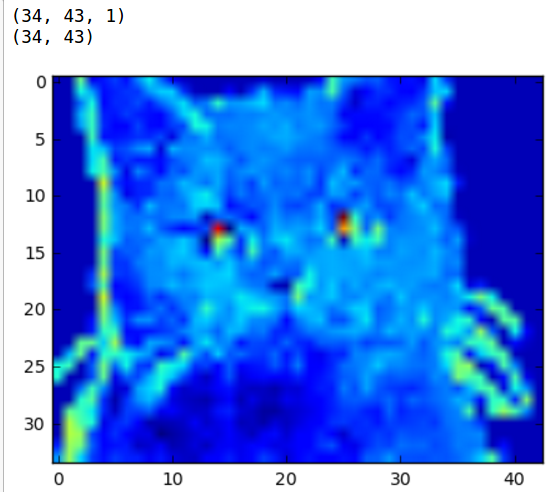
每个卷积层有 1 个过滤器
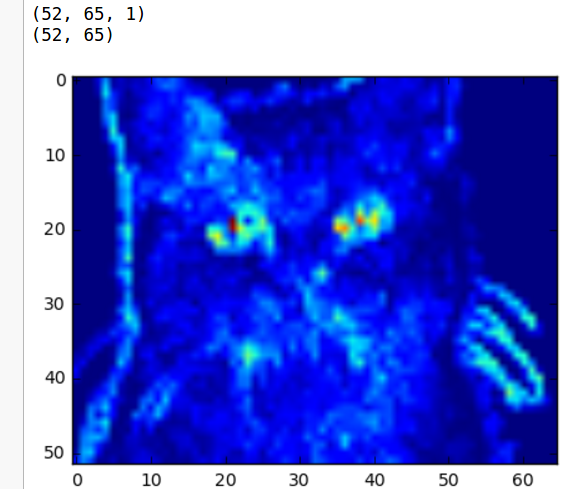
第一个卷积层有 3 个过滤器,第二个卷积层有 1 个过滤器
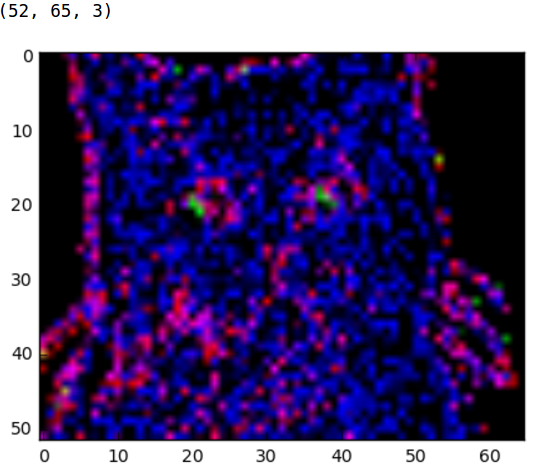
每个卷积层有 3 个过滤器
总结
鉴于卷积神经网络(ConvNet)能够提取图像的核心特征,并使用这些特征来识别包含类似特征的图像,因而十分强大。进一步通过我们后面的两个 CNN 范例,我们也可以看到该网络对诸如猫的胡须、鼻子和眼睛之类的区域关注较多。正是这些类型的特征将使得 CNN 能够将猫同鸟区分出来。
CNN 相当强大,尽管这些可视化效果并不完美,但是我希望它们能更好地帮助到像我一样仍然在学习 CNN 原理的人。
所有代码都可在此查询: https://github.com/erikreppel/visualizing_cnns
作者 Twitter:@programmer (https://twitter.com/programmer)
延伸资源
Andrej Karpathy's cs231n (http://cs231n.github.io/convolutional-networks/)
A guide to convolution arithmetic for deep learning by Vincent Dumoulin and Francesco Visin (https://arxiv.org/pdf/1603.07285v1.pdf)










![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)

