转载

CoreAnimation初探(一) —— 图形学基础

关于CoreAnimation

CoreAnimation是苹果提供的一套基于绘图的动画框架，下图是官方文档中给出的体系结构。

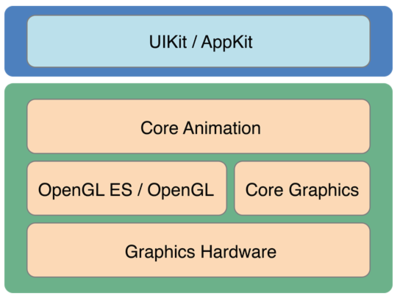
CoreAnimation所在位置

从图中可以看出，最底层是图形硬件(GPU)；上层是OpenGL和CoreGraphics，提供一些接口来访问GPU；再上层的CoreAnimation在此基础上封装了一套动画的API。最上面的UIKit属于应用层，处理与用户的交互。所以，学习CoreAnimation也会涉及一些图形学的知识，了解这些有助于我们更顺手的使用以及更高效的解决问题。本篇从以下几点简单整理了一些图形学的知识，以对其中原理有个概念上的认识。

什么是图形学

图形变换

曲线和曲面

1.什么是图形学

简单的说，计算机图形学是指用计算机产生对象图形输出的技术。更确切的说，是研究通过计算机将数据转换为图形，并在专门显示设备上显示的原理、方法和技术的学科。

举一个简单的例子，如果只提供给我们一个方法setPixel(x,y)用来点亮屏幕上坐标为(x,y)的像素点，如何在两点(x1,y1)、(x2,y2)之间画一条直线呢？（这是图形学研究的一个最基本问题：图形基元的显示。图形基元指一些基本的集合图形，如线段、圆、多边形等。）

我们最容易想到、也是最直接的方法便是计算出该直线在每个整数点对应的坐标值，四舍五入点亮与其最近的像素点（称为数值微分分析，DDA），如下图所示。

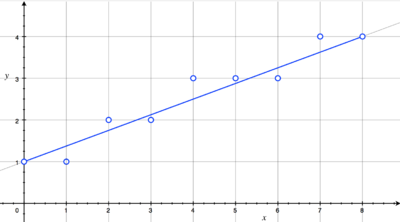
CoreAnimation初探(一) —— 图形学基础

直线扫描转换（斜率<1时）

但这种方法有很大的缺点：对于直线y=mx+b，我们在计算每个整数点坐标时，需要一次乘法和一次加法运算。而m、b都不一定是整数，所以更准确的说是浮点数乘法，这对于底层硬件实现是很伤的。

基于这种消除乘法和浮点数运算的思想便有了中心点画线法。

首先对于消除乘法运算，不必每次算坐标时都乘以斜率m，而是采用增量计算的方法；

而对于消除浮点数，则可以使用只含整数参数的直线方程计算：ax+by+c=0（这里a,b,c可以都为整数，因为我们的起点(x1,y1)和终点(x2,y2)是屏幕上的像素点一定都为整数，可以计算得出一个满足条件的整数方程：a=y1-y2, b=x2-x1, c=x1y2-x2y1）。

为方便讨论我们仍假设直线的斜率<1，在循环点亮路径上的像素点时，x坐标每次加1，y坐标每次要么加1要么不变取决于交点的位置。通过判断中心点位于直线的上方还是下方即可确定y坐标是否需要加1，如下。

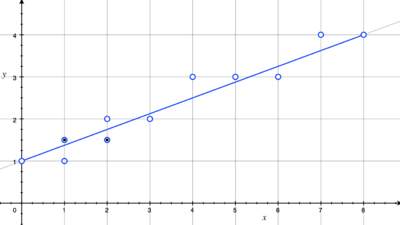
CoreAnimation初探(一) —— 图形学基础

中心点画线（斜率<1时）

我们可以构造判别式d=F(x+1,y+0.5)=a(x+1)+b(y+0.5)+c：d>0则中点在直线上方，反之在下方。用增量方式计算下一个中点的判别式：

若d>0，则y不变，d1=F(x+2,y+0.5)=a(x+2)+b(y+0.5)+c=d+a;

若d<0，则y+1，d2=F(x+2,y+1.5)=a(x+2)+b(y+1.5)+c=d+(a+b);

初值d0=F(x0+1,y0+0.5)=a(x0+1)+b(y0+0.5)+c=a+0.5b，由于只对d判别正负，可以用2d消除浮点数运算：

x=x0, y=y0, d=2*a+b;
d1=2*a, d2=2*(a+b);

setPixel(x,y);
while(x < x1)
{ 
    if(d < 0)
    {
        x++;
        y++;
        d+=d2;
    }
    else
    {
        x++;
        d+=d1;
    }
    setPixel(x,y);
}

中点画线法只包含整数变量且没有乘法运算，适合硬件实现。

还有一种更好的方法Bresenham画线算法，原理和中点画线法一样，不同的是使用交点到上下两个像素点的距离差作为判别式，同样采用增量计算，只含整数变量和加法、乘2(位移)运算，不再赘述。

以上便是图形学里最简单的图形基元——线段的扫描转换。为了方便底层硬件实现，这些算法都会尽可能的使用整数变量，使用增量计算减少乘除法(或转化为2的幂次通过位移实现)。按照这种套路不难理解圆、椭圆、多边形的扫描转换算法，这里就不一一探讨了。

有了这些图形基元后，通过变换、投影、裁剪、组合等方式便可以得到更加复杂的图形。

2.图形变换

计算机本身只能处理数字信息，各种图形在计算机系统内也是以数字的形式存在的。为了使被显示的对象数字化，就需要在被显示对象所在的空间中定义一个坐标系。

这里稍微区分一下几种不同坐标系的概念：

本体坐标系也称模型坐标系，为将对象数字化而建立的长度单位和坐标轴方向适合被现实对象描述的坐标系。一个复杂模型可能包含很多简单物体，可以分别对给他们建立一个方便建模的本体坐标系。
用户坐标系也称世界坐标系，我们对一个复杂模型建立了很多个本体坐标系，需要在一个大坐标系中将它们组合成一个整体，即世界坐标系。
观察坐标系，以观察姿态引入的坐标系。通常约定眼睛的位置为坐标原点，x轴水平向右，y轴竖直向上，z轴离开眼睛射向前方称为右手系，反之为左手系。
设备坐标系，为了最终将被描述的物体在显示器上显示或绘制出来，需要在显示器屏幕上定义一个二维直角坐标系。而为了达到与具体设备无关而引入的规范化设备坐标系规定坐标范围为均为0到1。

搞这么多坐标系，目的其实都是为了方便建模和处理，可见物体从建模到被显示出来的过程离不开坐标的变换。而为了统一地处理各种坐标变换，需要引入齐次坐标的概念。

齐次坐标表示法就是用n+1维向量表示一个n维向量。n维空间中的一个点(P1,P2,...,Pn)在n+1维空间中的齐次坐标表示为(hP1,hP2,...,hPn,h)。齐次坐标是不唯一的，当h=1时前n个坐标即为原n维空间中的点。

齐次坐标可以表示无穷远点，例如：(a,b,0)表示二维空间中直线bx-ay=0上的无穷远点。

应用齐次坐标可以有效地用矩阵运算将点从一个坐标系转换到另一个坐标系中。

可以理解为低维空间中的某个点p朝着某方向无限延伸到高一维空间中，延伸路径上的点p1,p2,......都映射到低维空间的p点上，p1,p2......在低维空间中都相当于原始点p。（个人理解。。）

为什么用齐次坐标就能统一处理变换，从表面上看增加一个维度可以将不同的变换放在同一个矩阵中表示，利用矩阵乘法的结合律也能轻松处理各种变换的组合，至于其中包含的理论原理就不做深入了，可以从变换矩阵的定义中简单体会一下：

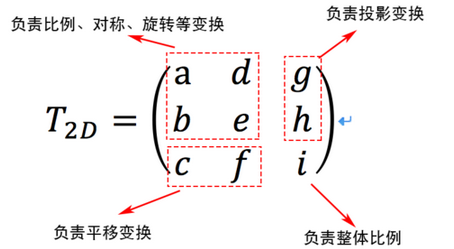
CoreAnimation初探(一) —— 图形学基础

二维齐次坐标变换矩阵形式

将每一行看做齐次坐标，如果是一个单位矩阵，则第一行(1,0,0)表示x轴上的无穷远点，第二行(0,1,0)表示y轴上的无穷远点，第三行(0,0,1)则表示坐标原点。所以当二维变换矩阵是单位矩阵时，相当于定义了二维空间中的直角坐标系。

将点p=(x,y,1)变换后的坐标记为p'=(x',y',1)，可得到下面的几何变换矩阵：

平移变换：x方向移动Tx，y方向移动Ty，则p'=(x+Tx, y+Ty, 1)

CoreAnimation初探(一) —— 图形学基础

二维平移变换矩阵

比例变换：x方向缩放Sx，y方向缩放Sy，则p'=(x·Sx, y·Sy, 1)

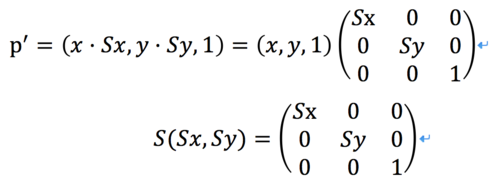
CoreAnimation初探(一) —— 图形学基础

二维比例变换矩阵

旋转变换：绕坐标原点逆时针旋转θ，则p'=(x·cosθ-y·sinθ, x·sinθ+y·cosθ, 1)

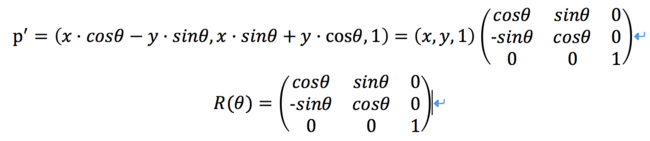
CoreAnimation初探(一) —— 图形学基础

二维旋转变换矩阵

这些变换都对应3×3的变换矩阵，根据矩阵乘法结合律可以组合出一些复杂的变换，例如绕任意点(x0,y0)旋转θ：可以先平移让其位于坐标原点，相对于原点作旋转变换后在平移回去：

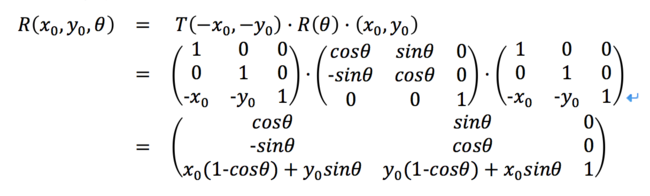
CoreAnimation初探(一) —— 图形学基础

绕点(x0,y0)旋转θ的变换矩阵

这便是用齐次坐标变换矩阵的方便之处。

类似的，可以推导出三维图形变换的齐次坐标变换矩阵，这里不再罗列公式了，我们从苹果提供的API中简单了解一下：

/* Homogeneous three-dimensional transforms. */
/* 齐次三维变换 */

/* 齐次三维变换的数据结构，为一个4×4矩阵 */
struct CATransform3D
{
  CGFloat m11, m12, m13, m14;
  CGFloat m21, m22, m23, m24;
  CGFloat m31, m32, m33, m34;
  CGFloat m41, m42, m43, m44;
};

typedef struct CATransform3D CATransform3D;

CATransform3D.h中提供的一些函数：

/* The identity transform: [1 0 0 0; 0 1 0 0; 0 0 1 0; 0 0 0 1]. */
/* 返回一个4×4单位矩阵 */
CA_EXTERN const CATransform3D CATransform3DIdentity
    CA_AVAILABLE_STARTING (10.5, 2.0, 9.0, 2.0);

/* Returns true if 't' is the identity transform. */
/* 判断变换矩阵t是否为单位矩阵 */
CA_EXTERN bool CATransform3DIsIdentity (CATransform3D t)
    CA_AVAILABLE_STARTING (10.5, 2.0, 9.0, 2.0);

/* Returns true if 'a' is exactly equal to 'b'. */
/* 判断变换矩阵a和b是否相等 */
CA_EXTERN bool CATransform3DEqualToTransform (CATransform3D a,
    CATransform3D b)
    CA_AVAILABLE_STARTING (10.5, 2.0, 9.0, 2.0);

/* 下面三个函数用来生成三维平移、比例、旋转变换矩阵 */

/* Returns a transform that translates by '(tx, ty, tz)':
 * t' =  [1 0 0 0; 0 1 0 0; 0 0 1 0; tx ty tz 1]. 
 * 返回一个三维平移变换矩阵 */
CA_EXTERN CATransform3D CATransform3DMakeTranslation (CGFloat tx,
    CGFloat ty, CGFloat tz)
    CA_AVAILABLE_STARTING (10.5, 2.0, 9.0, 2.0);

/* Returns a transform that scales by `(sx, sy, sz)':
 * t' = [sx 0 0 0; 0 sy 0 0; 0 0 sz 0; 0 0 0 1]. 
 * 返回一个三维比例变换矩阵 */
CA_EXTERN CATransform3D CATransform3DMakeScale (CGFloat sx, CGFloat sy,
    CGFloat sz)
    CA_AVAILABLE_STARTING (10.5, 2.0, 9.0, 2.0);

/* Returns a transform that rotates by 'angle' radians about the vector
 * '(x, y, z)'. If the vector has length zero the identity transform is
 * returned. 
 * 返回一个三维旋转变换矩阵，旋转轴为(x,y,z) */
CA_EXTERN CATransform3D CATransform3DMakeRotation (CGFloat angle, CGFloat x,
    CGFloat y, CGFloat z)
    CA_AVAILABLE_STARTING (10.5, 2.0, 9.0, 2.0);

/* 下面三个函数用来“对变换做变换”，??注意都是左乘 
 * 这里有点绕，比如对一个平移变换T做缩放变换S，得到的变换
 * 效果是先缩放在平移。我的理解是好比我们看3D电影时，一般
 * 都将3D镜片放在我们的近视镜前面，其实是对3D影像先进行处
 * 理，然后通过近视镜呈现给我们的眼睛，对于影片来说是先进
 * 行3D处理再做近视的变换；而对于眼镜来说，是它的近视变换
 * 之前被加上了一层3D处理。放在前面的变换才会影响到后面的
 * 变换，即对后面的变换“做了变换”。这里也是按着苹果注释中
 * 的定义强行理解了一波，不知道是不是这样，还请指教。。 */

/* Translate 't' by '(tx, ty, tz)' and return the result:
 * t' = translate(tx, ty, tz) * t. */
 * 对变换t进行(tx, ty, tz)的平移 */
CA_EXTERN CATransform3D CATransform3DTranslate (CATransform3D t, CGFloat tx,
    CGFloat ty, CGFloat tz)
    CA_AVAILABLE_STARTING (10.5, 2.0, 9.0, 2.0);

/* Scale 't' by '(sx, sy, sz)' and return the result:
 * t' = scale(sx, sy, sz) * t. 
 * 对变换t做(sx, sy, sz)的缩放 */
CA_EXTERN CATransform3D CATransform3DScale (CATransform3D t, CGFloat sx,
    CGFloat sy, CGFloat sz)
    CA_AVAILABLE_STARTING (10.5, 2.0, 9.0, 2.0);

/* Rotate 't' by 'angle' radians about the vector '(x, y, z)' and return
 * the result. If the vector has zero length the behavior is undefined:
 * t' = rotation(angle, x, y, z) * t. 
 * 对变换t做旋转angle，旋转轴为(x,y,z) */
CA_EXTERN CATransform3D CATransform3DRotate (CATransform3D t, CGFloat angle,
    CGFloat x, CGFloat y, CGFloat z)
    CA_AVAILABLE_STARTING (10.5, 2.0, 9.0, 2.0);

/* Concatenate 'b' to 'a' and return the result: t' = a * b. 
 * 组合a,b两个变换，返回矩阵a*b，相当于先做a变换再做b变换 */
CA_EXTERN CATransform3D CATransform3DConcat (CATransform3D a, CATransform3D b)
    CA_AVAILABLE_STARTING (10.5, 2.0, 9.0, 2.0);

/* Invert 't' and return the result. Returns the original matrix if 't'
 * has no inverse. 
 * 反向变换，相当于对矩阵求逆 */
CA_EXTERN CATransform3D CATransform3DInvert (CATransform3D t)
    CA_AVAILABLE_STARTING (10.5, 2.0, 9.0, 2.0);

3.曲线和曲面

我们开发时经常会用到或见到一个叫贝塞尔曲线的东西，它到底是什么，能做什么用，这里同样仅从概念上总结下计算机处理曲线和曲面的一些基础知识以及贝塞尔曲线的原理。

曲线和曲面的表示形式

我们都知道x^2+y^2=r^2 表示一个半径为r的圆，x^2+y^2=r^2叫做这个圆的方程；我们还可以用x=r·cosθ,y=r·sinθ表示这个圆，称为它的参数方程。

在空间曲线的参数表示中，曲线上每一个点的坐标均要表示成某个参数t的函数，即：x=x(t), y=y(t), z=z(t)
类似可以得出曲面的参数方程形式：x=x(u,v), y=y(u,v), z=z(u,v)
曲面的一般形式f(x,y,z)=0，而非参数形式的曲线可以定义为两个柱面的交线
1963年美国波音飞机公司的Fe

rguson首先提出将曲线曲面表示为参数的向量方程的方法。在此之前的画法几何和机械制图中，很难对自由型曲线进行清晰的表示。

插值和逼近

计算机中通常事先给定一些离散点（称为型值点），由这些点得出曲线的方法大体分为两类：一类要求曲线通过这些离散点，称为插值；另一类用这些点形成控制多边形来控制形状，称为逼近。

当型值点太多时，构造插值函数通过所有型值点是很困难的；或者当型值点本身带有误差时也没有必要寻找一个插值函数通过所有型值点，此时我们往往希望构造一条曲线在某种意义上逼近这些型值点。由型值点求插值或逼近曲线曲面的问题称为曲线或曲面的拟合。

贝塞尔曲线(Bézier curve)

法国雷诺(Renault)汽车公司的工程师Bézier于1971年发表了一种有控制多边形定义曲线的方法。设计员只要移动控制点就可以方便的修改曲线的形状，而且形状变化完全在意料之中，漂亮的解决了整体形状控制的问题。

贝塞尔曲线的定义其实并不复杂，我们用P0,P1,...,Pn表示给定的n+1个型值点（为什么是n+1，因为至少要有两个点才能构造线。。），而贝塞尔曲线的实质就是用n次多项式函数对这n+1个点进行混合：

CoreAnimation初探(一) —— 图形学基础

贝塞尔曲线的参数定义

所以，n次贝塞尔曲线其实就是一条n次参数多项式曲线。由于组合多项式的特殊性，贝塞尔曲线也有很多有意思的性质，比如：

起点和终点处的切线与控制多边形的第一和最后一边重合；
某一起点或终点的r阶导数由起点或终点以及它们的r个邻近的控制点决定，事实上正是由该性质推导出的贝塞尔曲线；
对称性：从起点出发和从终点出发得到同一条曲线。
分割递推性：由P0,P1,...,Pn所确定的n次贝塞尔曲线在点t的值可以由点P0,P1,...,Pn-1所确定的n-1次贝塞尔曲线在点t的值，与由点P1,P2,...,Pn所确定的n-1次贝塞尔曲线在点t的值通过线性组合求得：

CoreAnimation初探(一) —— 图形学基础