转载

Introduction: Tracking, Fusion and Deep learning for ADAS

作者：@强大的宇宙法德国大陆集团自动驾驶部门软件架构师海德堡大学博士candidate 汉诺威大学通信研究生西安电子科技大学电子信息本科主要从事多目标追踪以及深度学习，对智能驾驶以及计算机视觉算法领域有兴趣并且有自己的想法。

欢迎原链接转发，付费转载请前往 @强大的宇宙 的主页获取信息，盗版必究。

敬请关注和扩散本专栏及同名公众号，会邀请 全球知名学者 陆续发布运筹学、人工智能中优化理论等相关干货、知乎Live及行业动态：『运筹OR帷幄』大数据人工智能时代的运筹学

因为有计算机视觉和机器学习背景，上次和同事聊天中，同事建议我可以给一个小的Presentation来讲一下相关内容。于是我就花了一天时间准备了一下，给全组人做了一个1个半小时的汇报，大家讨论的也很热烈，功夫没白费。就把内容翻译成中文，一方面记录一下，另一方面也许有兴趣的朋友也可以了解一下。

题目很大，关于追踪，传感器融合和深度学习。就简单的讲一讲，这样受众面也会更广一些。

Tracking

卡尔曼滤波器可能很多人都听说过，它真的不是过滤咖啡的装置。它是一个optimal estimate (最优估计)。

什么时候需要用它呢？

举个例子，假如你要开车去机场接你的朋友，你的车上有三种传感器，加速度传感器，速度传感器，以及GPS定位系统。

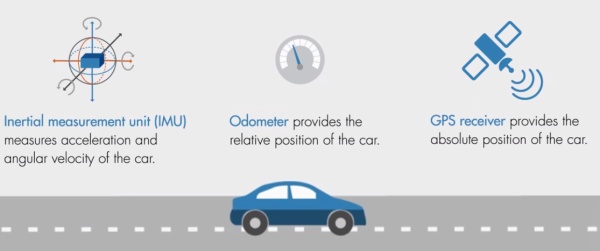
所有的这些传感器都能帮助你的汽车去寻找自己的位置。然而，这些传感器都有这样或那样的优点和缺点，都不完美。加速度传感器和速度仪都能实时更新，但是很容易累计错误。GPS可以提供绝对位置，但容易失去信号，噪声也很大。怎么办呢？

此时此刻，卡尔曼老先生发明了一个优美的算法，用这个算法就可以计算最优的汽车位置，即使传感器并不是很靠谱。

下图首先列出了tracking的精神纲领: 贝叶斯滤波 的数学公式。这个公式可以说是我最崇拜的一种看待世界的角度。 一切皆随机 。

我们把汽车位置以及所有的观测都看作是随机变量，有均值和方差。然后通过贝叶斯公式，可以很容易推导出以下公式，当然我们有一些假设，比如马尔科夫假设来简化计算难度。

如果我们此时假设所有变量皆满足高斯分布，并且所有的运动模型和观测模型都是线性的，那么我们就得到了卡尔曼滤波器。此时的update的过程，其实也可以看做是预测和测量的融合。

我们很容易找到卡尔曼滤波的公式，但看起来还是很复杂，到底公式的背后是什么，如何推导，相信很多人都打了退堂鼓。其实不难，我们可以拿一个1D的例子来说明。

如果都是高斯假设，那么我们如果按照贝叶斯公式，我们就相当于是将预测分布和测量分布直接相乘，也就是说直接让两个高斯密度函数相乘。我们会惊奇的发现，原来高斯乘以高斯，结果不仅仅是高斯，而且他的新的均值和方差竟然都是两个高斯方差的加权平均，也就是说，其实说白了，就是用各自的方差作为权值，重新更新了一下。然后其实卡尔曼增益不过就是两个权值的一种比例系数，方便后续计算而已。

So easy！

但是我们又要问了，那如果非高斯非线性，我们怎么追踪。呵呵，大师们早都已经解决了这个问题，我最喜欢的莫过于粒子滤波。背后的思想让我拍手称绝。

要了解粒子滤波，必须先了解蒙特卡洛方法。当年去摩纳哥的蒙特卡洛赌场小玩老虎机，确实好玩又刺激。不过小赌怡情，大赌伤身，就玩了5欧，最后输完了。

回归正题，假设你要计算圆周率，你想简单算，不想太复杂。那么你可以用笔在纸上画一个正方形，然后用圆规画一个四分之一内接圆。接下来就是见证奇迹的时刻，你抓一把豆子，均匀的撒在纸上矩形区域，并数落在圆形内部的豆子数目，和落在外面的豆子数目。然后你就可以根据豆子数目的比例，简单的计算出圆周率。是不是很神奇！

同样的思想用在追踪问题上，就更不可思议了。你可以用一些样本点来代替你需要的复杂分布，然后你就不再需要用这个复杂的分布来计算了，只需要这些采样的样本点就可以了。无论线性变换还是非线性变换，都很轻易的就可以计算出样本点的变换，然后通过变换后的样本点来统计新的均值和方差，就完成了复杂分布的非线性变换过程，够简单够暴力？哈哈，是的。

当然代价就是你要计算每一个样本点，计算开销很大。

Multi-sensor fusion

传感器融合这个topic太火了，现在硬件平台上集成了一圈各式各样的传感器，怎么博采众长海纳百川，是个问题。

不过都难不倒贝叶斯老先生，在贝叶斯的眼里，这些都是浮云。

举个例子，雷达和红外摄像机的融合。雷达距离探测的非常准确，但是红外摄像机方位角很准确，那么如何结合两者的优点呢。我们采用融合measurement likelihood方法来做，因为假设两个传感器都是条件独立的，意味着传感器并不互相影响。那么我们只需要简单的将两个各自的likelihood的函数相乘，然后我们就会得到新的统一的likelihood function. 神奇的发现，最终的分布函数形状变的更小更尖了，意味着新的likelihood具有更好的方位角和距离信息了。

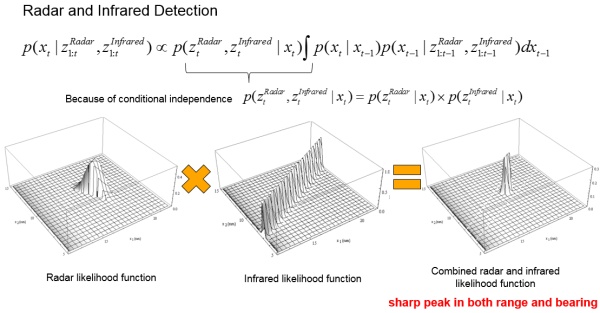
是不是很神奇？针对之前汽车的例子，我们也可以融合GPS, 加速度传感器以及速度传感器一起，做到博采众长的追踪。

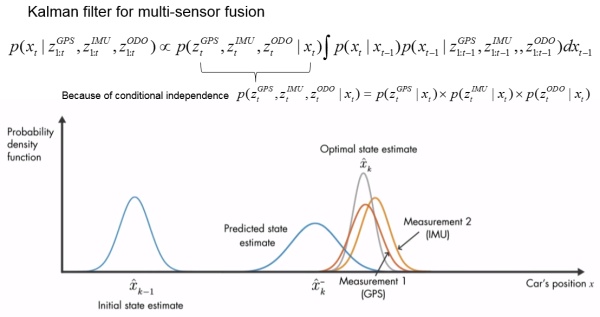
Deep learning

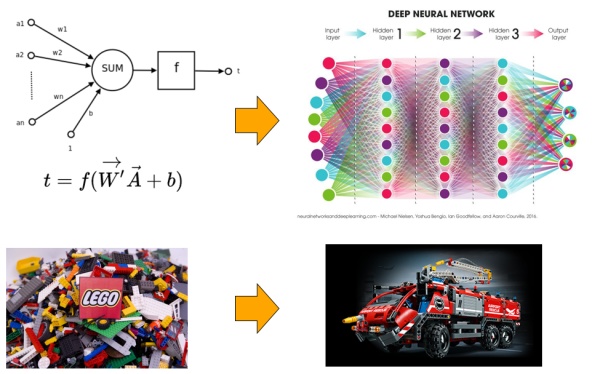
神经网络已经有年头了，但都没有像最近这么火，无敌了。我记得我第一次接触是在本科的时候，数模竞赛的时候。其实神经网络应该就是一种函数模拟器，只要你组织好input data和output data, 剩下的就交给神经网络去学习吧。当然你也要设计一个优美的loss function来告诉神将网络做人的底线和原则。

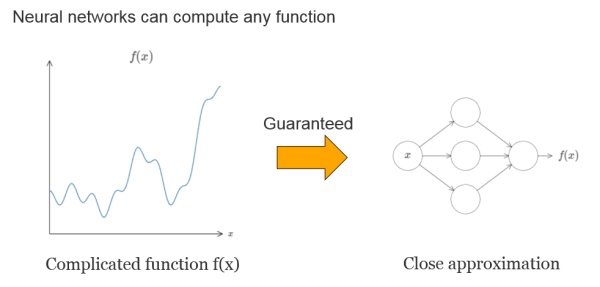
神经元是神经网络的基本组成单位，多输入，单输出，加一个非线性激活函数，如此简单。就像乐高玩具一样，你可以随意组合你的神经元们，让他变得更加强大和不可思议。这就是深度神经网络。

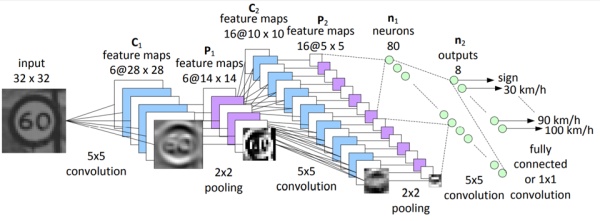
目前最热门的应用还属CNN, 卷积神经网络。如下图所示，输入是交通限速标志，输出是限速的具体速度值。当然要用反向传播算法来update神经网络里神经元的权重，下面这个图就非常直观明了:

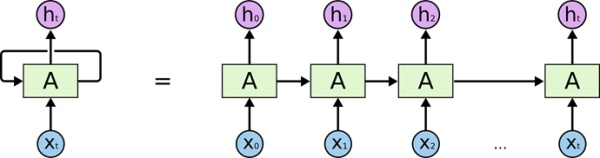
另外一个其实应该更有意思的神经网络结构RNN (Recurrent Neural Network), 递归神经网络。有记忆的神经网络，因为有feedback的过程，所以很适合做序列数据的预测。之前有很长时间在用它来做tracking，效果一般但觉得很有前途。当然用它可以写诗，写音乐，或者写代码，以及翻译等等工作，很像人类的思维方式，这恐怕才是人工智能的未来。