经验分享 | 记一次RSA破解
最近好久没更新博客，因为在忙着考雅思还有一直也在看CTF（=_=上个星期玩了一下腾讯的CTF……这酸爽，我一直都认为比赛是最容易提升自己实力的一种途径，上次比赛也发现了自己的不足，继续努力吧少年），今天看了一天的RSA算法。以前在上课的时候，记得老师光讲这个算法就讲了有两堂课。现在在看一下其实也不是很难（别骗自己了=_=），所以写这篇文章记录一下，顺便加深一下自己的印象。
0×1
首先开始之前我们要补充一下关于RSA的一些常识。
（1）选择一对不同的、足够大的素数p，q。
（2）计算n=pq。
（3）计算f(n)=(p-1)(q-1)，同时对p, q严加保密，不让任何人知道。
（4）找一个与f(n)互质的数e，且1<e<f(n)。
（5）计算d，使得de≡1 modf(n)。这个公式也可以表达为(d*e-1)% f(n)=0
这里要解释一下，≡是数论中表示同余的符号。公式中，≡符号的左边必须和符号右边同余，也就是两边模运算结果相同。
显而易见，不管f(n)取什么值，符号 右边1 mod f(n)的结果都等于1；符号的左边d与e的乘积做模运算后的结果也必须等于1。
这就需要计算出d的值，让这个同余等式能够成立。
（6）公钥KU=(e,n)，私钥KR=(d,n)。
（7）加密时，先将明文变换成0至n-1的一个整数M。若明文较长，可先分割成适当的组，然后再进行交换。设密文为C，
则加密过程为：C≡M^e(mod n)。
（8）解密过程为：M≡C^d(mod n)。
同余：数论中的重要概念。给定一个正整数m，如果两个整数a和b满足（a-b）能够被m整除，即（a-b）/m得到一个整数，那么就称整数a与b对模m同余。
记作a≡b(mod m)。对模m同余是整数的一个等价关系。
有了上面的RSA基础可以知道RSA中的。
p: 第一个大素数
q: 第二个大素数
模数n: n = p*q
f(n): (p-1)*(q-1)
公钥指数e: 与 f(n)互质, 且 1 < e < f(n)
私钥指数d: 满足e * d ≡ 1 (mod f(n))
公钥 = {n, e}，一般公开
私钥 = {d, e}
0×2
就拿实验吧上面的一个题做这个例子吧因为最近也一直在玩CTF。
http://ctf5.shiyanbar.com/crypto/RSAROLL.txt
第一行我们看到了这样一组数，直觉告诉我们这个很有可能是公钥(当然也不排除出题师傅直接把私钥给你，这样出题师傅是不是就太可爱了呀)。
{920139713,19}
根据我们上面补充的知识知道要按照步骤来获取私钥。
(1) n = 920139713 e =19
(2) 这时候我们要将整数n分解为两个素数，我们可以使用在线网站直接来获取。
http://www.factordb.com/index.php
当然我们可以写代码来实现
如下：defdivde(n):
start =2
whilestart < math.sqrt(n):
if (n%start==0):
record = start
print(“大整数可以分解为:”,str(start),str(int(n/base)))
break
base+=1
return (start,int(n/base))
(3) 经过上面的操作我们可以获得
p = 18443,q =49891,f(n) = (p-1)*(q-1)/p，q 是上n分解的两个质数，f(n)是欧拉函数
(4) 根据我们现在已经获得的条件以及前面补充的RSA知识我们知道只要找到一个满足e * d ≡ 1 (mod f(n)) 这个方程式的d，我们就成功获取的私钥(于是我就自己写了一个函数跑了一下，跑了好长时间仍然没有结果，在我快要放弃的时候我忽然想到了gmpy2，其中有一个神奇的函数)
(g,d,_) = gcdext(e,f(n)) //不知道为什么是这种格式但是它的效果是与e * d ≡ 1 (mod f(n)) 使用此函数只用了不到一秒的时间就获得了私钥d= 96849619
(5) 至此成功拿到了私钥，剩下的就剩解密密文
利用pow(i,d,n))解密密文//这里的i就是密文，d是我们刚才获取的私钥，n公钥如下图一
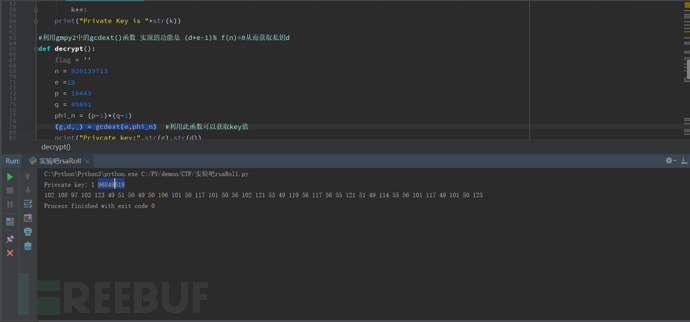
图一获取的是ASCII
(6) 最后将ASCII转化为相应的字符 (这里我用了自己写的一个小脚本工具)
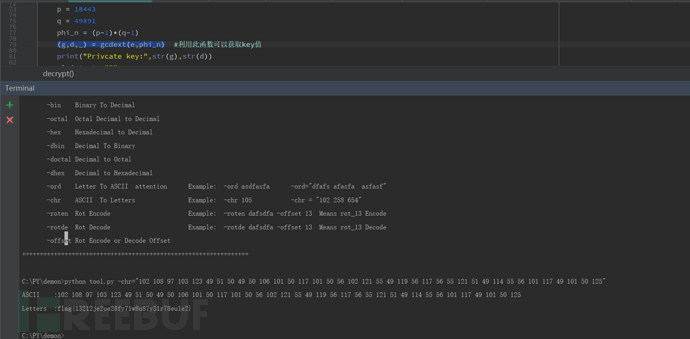
图二将ASCII转化为字符
0×3 代码部分
#-*- coding:utf-8 -*-
from gmpy2 import *
from Crypto.Util.number import *
利用gmpy2中的gcdext()函数实现的功能是 (d*e-1)% f(n)=0从而获取私钥d
def decrypt():
flag = ''
n= 920139713
e=19
p= 18443
q= 49891
phi_n = (p-1)*(q-1)
(g,d,_) = gcdext(e,phi_n) #利用此函数可以获取私钥d值
print("Privcate key:",str(g),str(d))
plaintext =""" 704796792
752211152
274704164
18414022
368270835
483295235
263072905
459788476
483295235
459788476
663551792
475206804
459788476
428313374
475206804
459788476
425392137
704796792
458265677
341524652
483295235
534149509
425392137
428313374
425392137
341524652
458265677
263072905
483295235
828509797
341524652
425392137
475206804
428313374
483295235
475206804
459788476
306220148
"""
plaintext = plaintext.split()
for i in plaintext:
#利用pow(l,d,n) l的d次方然后取n的余数
i = int(i)
print((pow(i,d,n)),end=' ')
if __name__=='__main__':
decrypt()
0×4 后记
嘻嘻，前段时间女朋友闹着分手，上个星期她又打电话说对不起，我们重新和好吧。嗯~ o(*￣▽￣*)o知错就改还是好同志嘛！之前好伤心呢，现在一起都过去了。我会以更加昂扬的斗志生活。
后后记+_+ pwn好难呀，不会呀！要多多看看这方面的文章。
*本文作者：白帽子马振华，转载请注明FreeBuf.COM
正文到此结束
热门推荐
相关文章
近期评论
-
文章和留言都翻到11页了 没有OOM
-
-
朋友，翻页到11页，及以后，会出现OOM，无法访问
-
-
搞个gitee的项目
-
-
版本号是多少，你可以下载哪个代码仓库，jdk选1.8 直接跑就行
-
-
-
Loading...
![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)
