转载

从字符级的语言建模开始，了解语言模型与序列建模的基本概念

循环神经网络（RNN）模型常用于训练这种语言模型，因为它们使用高维隐藏状态单元处理信息的能力非常强大，建模长期依赖关系的能力也非常强。任意语言模型的主要目的都是学习训练文本中字符／单词序列的联合概率分布，即尝试学习联合概率函数。例如，如果我们试图预测一个包含 T 个词的单词序列，那么我们试图获取令联合概率 P(w_1, w_2, …, w_T) 最大的词序列，等价于所有时间步 (t) 上条件概率的累乘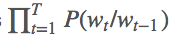：从字符级的语言建模开始，了解语言模型与序列建模的基本概念。

本文描述了字符级的语言模型，其中几乎所有概念都适用于其它语言模型，如单词级的语言模型等。字符级语言模型的主要任务是根据之前的所有字符预测下一个字符，即逐个字符地生成文本内容。更正式地来说，给出训练序列 (x^1,…,x^T)，RNN 使用输出向量序列 (o^1,…,o^T) 来获取预测分布 P(x^t|x^t−1)=softmax(o^t)。

下面我用我的姓氏（imad）为例介绍字符级语言模型的运行过程（该示例的详情见图 2）。

1. 我们首先用语料库中所有名字的字母（去掉重复的字母）作为关键词构建一个词汇词典，每个字母的索引从 0 开始（因为 Python 的索引也是从零开始），按升序排列。以 imad 为例，词汇词典应该是：{「a」: 0,「d」: 1,「i」: 2,「m」: 3}。因此，imad 就变成整数列表：[2, 3, 0, 1]。

2. 使用词汇词典将输入和输出字符转换成整型数列。本文中，我们假设所有示例中从字符级的语言建模开始，了解语言模型与序列建模的基本概念。因此，y=「imad」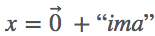，。换言之，x^t+1=y^t，y=[2,3,0,1]，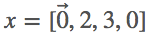

3. 对于输入中的每一个字符：

将输入字符转换成 one-hot 向量。注意第一个字符的转换过程。
计算隐藏状态层。
计算输出层，然后将计算结果传入 softmax 层，获得的结果就是概率。
把时间步 (t) 的目标字符作为时间步 (t+1) 的输入字符。
返回步骤 a，重复该过程，直到结束名字中的所有字母。

模型的目标是使概率分布层中的绿色数值尽可能大，红色数值尽可能小。原因在于概率趋近于 1 时，真正的索引具备最高的概率。我们可以使用交叉熵来评估损失，然后计算损失函数关于所有参数损失的梯度，并根据与梯度相反的方向更新参数。不断重复该过程并迭代地调整参数，这样模型就能够使用训练集中的所有名字，根据之前的字符预测后一个字符。注意：隐藏状态 h^4 具备所有之前字符的信息。

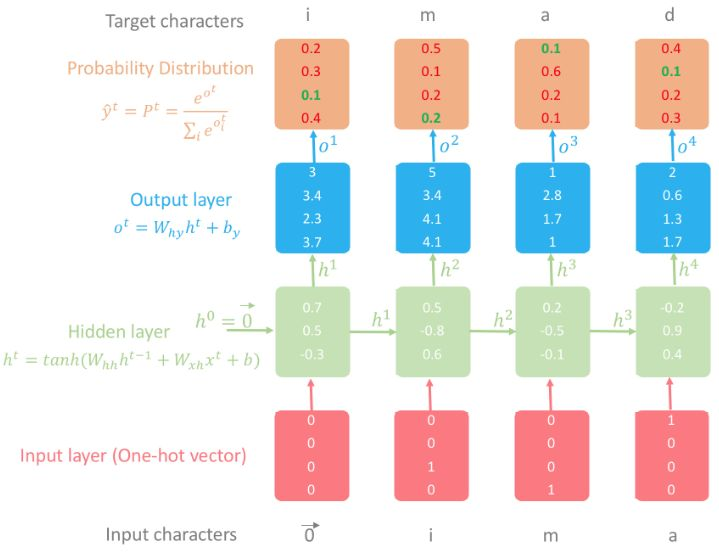
从字符级的语言建模开始，了解语言模型与序列建模的基本概念

图 2：使用 RNN 的字符级语言模型图示。

注意：为简洁起见，我删除了所有 Python 函数的文档注释，也没有包含一些无益于理解主要概念的函数。

notebook 和 script 地址：https://nbviewer.jupyter.org/github/ImadDabbura/blog-posts/blob/master/notebooks/Character-LeveL-Language-Model.ipynb

https://github.com/ImadDabbura/blog-posts/blob/master/scripts/character_level_language_model.py

训练

我们使用的数据集有 5163 个名字：4275 个男性名字，以及 1219 个女性名字，其中有 331 个名字是中性的。我们将使用多对多的 RNN 架构来训练字符级语言模型，其中输入（T_x）的时间步等于输出（T_y）的时间步。换句话说，输入和输出的序列是同步的（详见图 3）。

数据集地址：http://deron.meranda.us/data/census-derived-all-first.txt

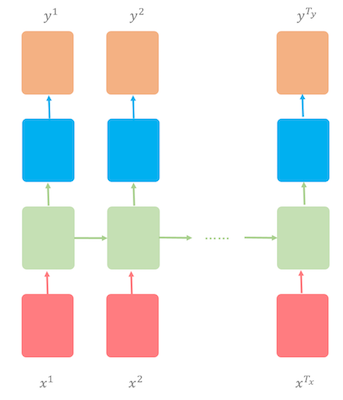
从字符级的语言建模开始，了解语言模型与序列建模的基本概念

图 3：多对多的 RNN 架构。

该字符级语言模型将在名字数据集上训练，然后我们可以使用该模型生成一些有趣的名字。

在这一节中，我们将介绍 4 个主要内容：

1 前向传播

2 反向传播

3 采样

4 拟合模型

前向传播

我们将使用随机梯度下降（SGD），其中每个 Batch 只包含一个样本。也就是说，RNN 模型将从每个样本（名字）中分别进行学习，即在每个样本上运行前向和反向传播，并据此更新参数。以下是前向传播所需步骤：

使用全部小写字母（无重复）构建词汇词典：
创建不同字符的索引词典，使每个字符以升序对应索引。例如，a 的索引是 1（因为 Python 的索引是从 0 开始，我们将把 0 索引保存为 EOS「/n」），z 的索引是 26。我们将使用该词典将名字转换成整数列表，其中的每个字母都用 one-hot 向量来表示。
创建一个字符词典的索引，使索引映射至字符。该词典将用于将 RNN 模型的输出转换为字符，然后再翻译成名字。
初始化参数：将权重初始化为从标准正态分布中采样的较小随机数值，以打破对称性，确保不同的隐藏单元学习不同的事物。另外，偏置项也要初始化为 0。
W_hh：权重矩阵，连接前一个隐藏状态 h^t−1 和当前的隐藏状态 h^t。
W_xh：权重矩阵，连接输入 x^t 和隐藏状态 h^t。
b：隐藏状态偏置项向量。
W_hy：权重矩阵，连接隐藏状态 h^t 与输出 o^t。
c：输出偏置项向量。
将输入 x^t 和输出 y^t 分别转换成 one-hot 向量：one-hot 向量的维度是 vocab_size x 1，除了在字符处的索引是 1，其他都是 0。在我们的案例中，x^t 和 y^t 一样需要向左移一步。例如，如果我们使用「imad」作为输入，那么 y=[3,4,1,2,0]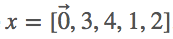，。注意：，索引不是 0。此外，我们还使用「/n」作为每个名字的 EOS（句子／名字末尾），这样 RNN 可以将「/n」学习为任意其它字符。这会帮助网络学习什么时候停止生成字符。因此，所有名字的最后一个目标字符都将是表示名字末尾的「/n」。
使用以下公式计算隐藏状态：

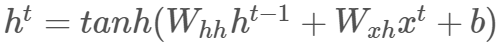
从字符级的语言建模开始，了解语言模型与序列建模的基本概念

注意我们使用双曲正切从字符级的语言建模开始，了解语言模型与序列建模的基本概念作为非线性函数。主要优势是双曲正切函数在一定范围内近似于恒等函数。

用以下公式计算输出层：

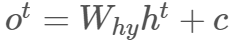
从字符级的语言建模开始，了解语言模型与序列建模的基本概念

将输出传输至 softmax 层，以归一化输出，这样我们可以将它表达为概率，即所有输出都在 0 和 1 之间，总和为 1。以下是 softmax 公式：

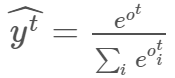
softmax 层和输出层的维度相同，都是 vocab_size x 1。因此，y^t[i] 表示时间步 (t) 下索引 i 对应字符为预测字符的概率。

如前所述，字符级语言模型的目标是最小化训练序列的负对数似然。因此，时间步 (t) 的损失函数和所有时间步的总损失为：

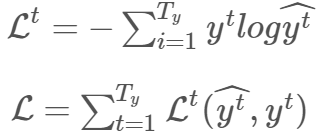
从字符级的语言建模开始，了解语言模型与序列建模的基本概念

由于我们使用 SGD，因此损失函数的一阶导作为下降方向会带有噪声，且会存在振荡现象，因此使用指数加权平均法消除噪声是一个不错的方法。

将目标字符 y^t 作为下一个输入 x^t+1，直到完成该序列。

# Load packages
import os

import numpy as np

os.chdir("../scripts/")
from character_level_language_model import (initialize_parameters,
                                            initialize_rmsprop,
                                            softmax,
                                            smooth_loss,
                                            update_parameters_with_rmsprop)


def rnn_forward(x, y, h_prev, parameters):
    """Implement one Forward pass on one name."""
    # Retrieve parameters
    Wxh, Whh, b = parameters["Wxh"], parameters["Whh"], parameters["b"]
    Why, c = parameters["Why"], parameters["c"]

    # Initialize inputs, hidden state, output, and probabilities dictionaries
    xs, hs, os, probs = {}, {}, {}, {}

    # Initialize x0 to zero vector
    xs[0] = np.zeros((vocab_size, 1))

    # Initialize loss and assigns h_prev to last hidden state in hs
    loss = 0
    hs[-1] = np.copy(h_prev)

    # Forward pass: loop over all characters of the name
    for t in range(len(x)):
        # Convert to one-hot vector
        if t > 0:
            xs[t] = np.zeros((vocab_size, 1))
            xs[t][x[t]] = 1
        # Hidden state
        hs[t] = np.tanh(np.dot(Wxh, xs[t]) + np.dot(Whh, hs[t - 1]) + b)
        # Logits
        os[t] = np.dot(Why, hs[t]) + c
        # Probs
        probs[t] = softmax(os[t])
        # Loss
        loss -= np.log(probs[t][y[t], 0])

    cache = (xs, hs, probs)

    return loss, cache

反向传播

在基于 RNN 的模型上使用的基于梯度的技术被称为随时间的反向传播（Backpropagation Through Time，BPTT）。我们从最后的时间步 T 开始，计算关于全部时间步的所有参数的反向传播梯度，并将它们都加起来（如图 4 所示）。

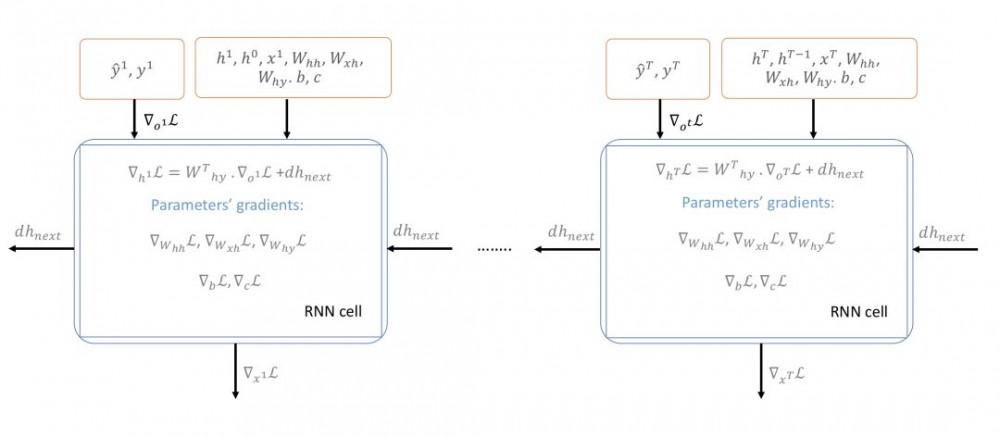
从字符级的语言建模开始，了解语言模型与序列建模的基本概念

图 4：随时间的反向传播（BPTT）。

此外，由于已知 RNN 有很陡峭的梯度变化，梯度可能会突然变得非常大然后使原来训练得到的进展功亏一篑，即使使用了适应性学习方法如 RMSProp。其原因是梯度是损失函数的线性近似，可能无法捕捉在评估的点之外的其它信息，例如损失曲面的曲率。因此，通常在实践中会将梯度限制在 [-maxValue, maxValue] 区间内。在这里，我们将把梯度限制在 [-5,5] 上。这意味着如果梯度小于-5 或者大于 5，它将分别被截断为-5 和 5。以下是所有时间步上用于计算损失函数对所有参数的梯度所需的公式。

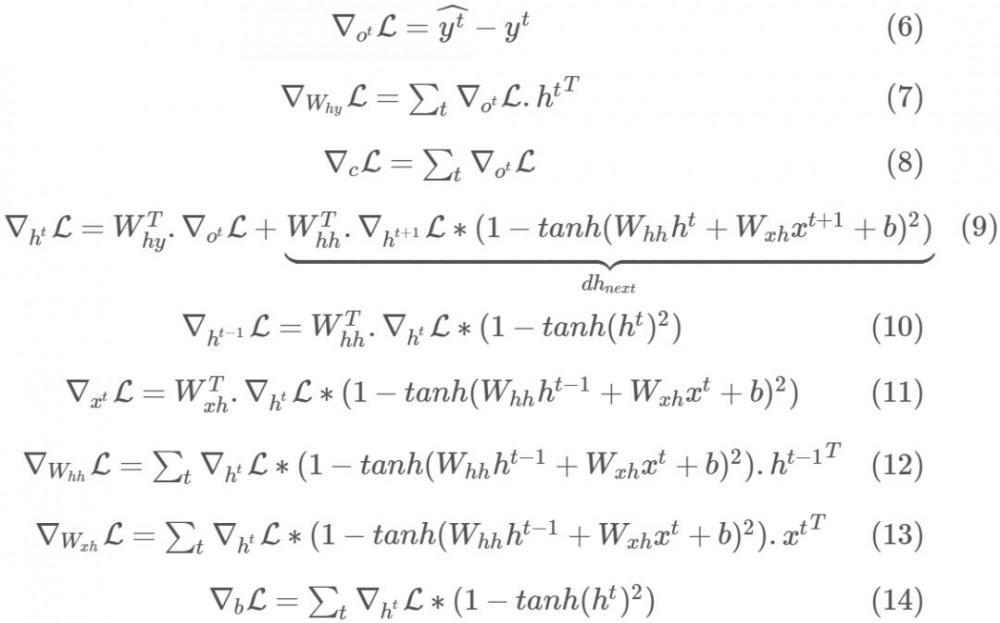
从字符级的语言建模开始，了解语言模型与序列建模的基本概念

注意，在最后的时间步 T，我们将初始化 dh_next 为 0，因为其无法在未来得到任何更新值。由于 SGD 可能存在很多振荡，为了在每个时间步稳定更新过程，我们将使用其中一种适应性学习率的优化方法。具体来说，我们将使用 RMSProp，该方法能够获得可接受的性能。

def clip_gradients(gradients, max_value):
    """
    Implements gradient clipping element-wise on gradients to be between the
    interval [-max_value, max_value].
    """
    for grad in gradients.keys():
        np.clip(gradients[grad], -max_value, max_value, out=gradients[grad])

    return gradients


def rnn_backward(y, parameters, cache):
    """
    Implements Backpropagation on one name.
    """
    # Retrieve xs, hs, and probs
    xs, hs, probs = cache

    # Initialize all gradients to zero
    dh_next = np.zeros_like(hs[0])

    parameters_names = ["Whh", "Wxh", "b", "Why", "c"]
    grads = {}
    for param_name in parameters_names:
        grads["d" + param_name] = np.zeros_like(parameters[param_name])

    # Iterate over all time steps in reverse order starting from Tx
    for t in reversed(range(len(xs))):
        dy = np.copy(probs[t])
        dy[y[t]] -= 1
        grads["dWhy"] += np.dot(dy, hs[t].T)
        grads["dc"] += dy
        dh = np.dot(parameters["Why"].T, dy) + dh_next
        dhraw = (1 - hs[t] ** 2) * dh
        grads["dWhh"] += np.dot(dhraw, hs[t - 1].T)
        grads["dWxh"] += np.dot(dhraw, xs[t].T)
        grads["db"] += dhraw
        dh_next = np.dot(parameters["Whh"].T, dhraw)
        # Clip the gradients using [-5, 5] as the interval
        grads = clip_gradients(grads, 5)

    # Get the last hidden state
    h_prev = hs[len(xs) - 1]

    return grads, h_prev

采样

正是采样过程使得用 RNN 在每个时间步生成的文本变得有趣和有创造性。在每个时间步 (t)，给定所有的已有字符，RNN 可输出下一个字符的条件概率分布，即 P(c_t|c_1,c_2,…,c_t−1)。假设我们在时间步 t=3，并尝试预测第三个字符，其条件概率分布为 P(c_3/c_1,c_2)=(0.2,0.3,0.4,0.1)。其中有两种极端情况：

最大熵：字符会使用均匀概率分布进行选取；这意味着词汇表中的所有字符都是同等概率的。因此，我们最终将在选取下一个字符的过程中达到最大随机性，而生成的文本也不会有意义。
最小熵：在每个时间步，拥有最高条件概率的字符将会被选取。这意味着下一个字符的选取将基于训练中的文本和已学习的参数。因此，生成的命名将是有意义的和有真实性的。

随着随机性的增大，文本将逐渐失去局部结构；然而，随着随机性的减小，生成的文本将变得更具真实性，并逐渐开始保留其局部结构。在这里，我们将从模型生成的分布中采样，该分布可被视为具有最大熵和最小熵之间的中等级别的随机性（如图 5 所示）。在上述分布中使用这种采样策略，索引 0 有 20% 的概率被选取，而索引 2 有 40% 的概率被选取。

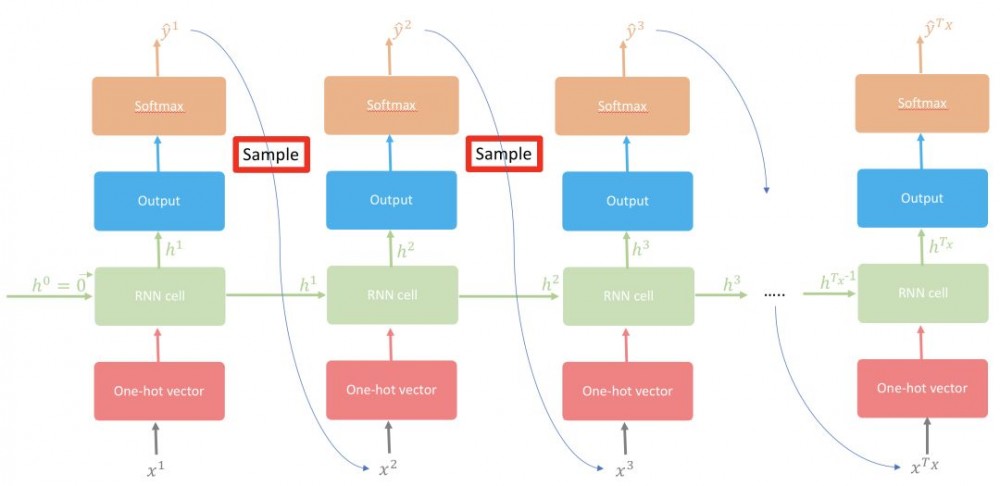
从字符级的语言建模开始，了解语言模型与序列建模的基本概念

图 5：采样：使用字符级语言建模预测下一个字符的图示。因此，采样过程将在测试时用于一个接一个地生成字符。

def sample(parameters, idx_to_chars, chars_to_idx, n):

   """
    Implements sampling of a squence of n characters characters length. The
    sampling will be based on the probability distribution output of RNN.
    """
    # Retrienve parameters, shapes, and vocab size
    Whh, Wxh, b = parameters["Whh"], parameters["Wxh"], parameters["b"]
    Why, c = parameters["Why"], parameters["c"]
    n_h, n_x = Wxh.shape
    vocab_size = c.shape[0]

    # Initialize a0 and x1 to zero vectors
    h_prev = np.zeros((n_h, 1))
    x = np.zeros((n_x, 1))

    # Initialize empty sequence
    indices = []
    idx = -1
    counter = 0
    while (counter <= n and idx != chars_to_idx["/n"]):
        # Fwd propagation
        h = np.tanh(np.dot(Whh, h_prev) + np.dot(Wxh, x) + b)
        o = np.dot(Why, h) + c
        probs = softmax(o)

        # Sample the index of the character using generated probs distribution
        idx = np.random.choice(vocab_size, p=probs.ravel())

        # Get the character of the sampled index
        char = idx_to_chars[idx]

        # Add the char to the sequence
        indices.append(idx)

        # Update a_prev and x
        h_prev = np.copy(h)
        x = np.zeros((n_x, 1))
        x[idx] = 1

        counter += 1
    sequence = "".join([idx_to_chars[idx] for idx in indices if idx != 0])

    return sequence

拟合模型

在介绍了字符级语言建模背后的所有概念/直觉思想之后，接下来我们开始拟合模型。我么将使用 RMSProp 的默认超参数设置，并迭代地运行模型 100 次。在每次迭代中，我们将输出一个采样的命名，并平滑损失函数，以观察生成的命名如何（随着迭代数的增加和梯度的下降）变得越来越有趣。当模型拟合完成后，我们将画出损失函数并生成一些命名。

def model(
        file_path, chars_to_idx, idx_to_chars, hidden_layer_size, vocab_size,
        num_epochs=10, learning_rate=0.01):
    """Implements RNN to generate characters."""
    # Get the data
    with open(file_path) as f:
        data = f.readlines()
    examples = [x.lower().strip() for x in data]

    # Initialize parameters
    parameters = initialize_parameters(vocab_size, hidden_layer_size)

    # Initialize Adam parameters
    s = initialize_rmsprop(parameters)

    # Initialize loss
    smoothed_loss = -np.log(1 / vocab_size) * 7

    # Initialize hidden state h0 and overall loss
    h_prev = np.zeros((hidden_layer_size, 1))
    overall_loss = []

    # Iterate over number of epochs
    for epoch in range(num_epochs):
        print(f"/033[1m/033[94mEpoch {epoch}")
        print(f"/033[1m/033[92m=======")

        # Sample one name
        print(f"""Sampled name: {sample(parameters, idx_to_chars, chars_to_idx,
            10).capitalize()}""")
        print(f"Smoothed loss: {smoothed_loss:.4f}/n")

        # Shuffle examples
        np.random.shuffle(examples)

        # Iterate over all examples (SGD)
        for example in examples:
            x = [None] + [chars_to_idx[char] for char in example]
            y = x[1:] + [chars_to_idx["/n"]]
            # Fwd pass
            loss, cache = rnn_forward(x, y, h_prev, parameters)
            # Compute smooth loss
            smoothed_loss = smooth_loss(smoothed_loss, loss)
            # Bwd pass
            grads, h_prev = rnn_backward(y, parameters, cache)
            # Update parameters
            parameters, s = update_parameters_with_rmsprop(
                parameters, grads, s)

        overall_loss.append(smoothed_loss)

    return parameters, overall_loss

# Load names data = open("../data/names.txt", "r").read() # Convert characters to lower case data = data.lower() # Construct vocabulary using unique characters, sort it in ascending order, # then construct two dictionaries that maps character to index and index to # characters. chars = list(sorted(set(data))) chars_to_idx = {ch:i for i, ch in enumerate(chars)} idx_to_chars = {i:ch for ch, i in chars_to_idx.items()} # Get the size of the data and vocab size data_size = len(data) vocab_size = len(chars_to_idx) print(f"There are {data_size} characters and {vocab_size} unique characters.") # Fitting the model parameters, loss = model("../data/names.txt", chars_to_idx, idx_to_chars, 100, vocab_size, 100, 0.01) # Plotting the loss plt.plot(range(len(loss)), loss) plt.xlabel("Epochs") plt.ylabel("Smoothed loss");

There are 36121 characters and 27 unique characters. Epoch 0 ======= Sampled name: Nijqikkgzst Smoothed loss: 23.0709 Epoch 10 ======= Sampled name: Milton Smoothed loss: 14.7446 Epoch 30 ======= Sampled name: Dangelyn Smoothed loss: 13.8179 Epoch 70 ======= Sampled name: Lacira Smoothed loss: 13.3782 Epoch 99 ======= Sampled name: Cathranda Smoothed loss: 13.3380

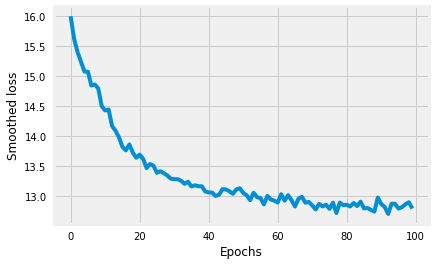
从字符级的语言建模开始，了解语言模型与序列建模的基本概念