转载

通过 GPU 加速浏览器浮点数计算能力

这是一个颜值即正义的年代，可谁曾知道，一副酷炫的 3D 画面背后，是难以想象的，数以吨计的数学运算。为了完成这些繁重的任务，显卡(GPU)提供了强有力的计算加速支持，这种加速能力并不仅仅局限在图像渲染领域，在科学计算，AI，区块链都有广泛地使用。如 AMD 下的 OpenCL、Nvida 的 CUDA 都是可以将 GPU 用于通用数学计算的项目。

通过 GPU 加速浏览器浮点数计算能力

直到 WebGL 技术出现，浏览器也解锁了这种加速 “福利”，我们终于可以在 web 页面中看到 3D 场景了。那浏览器是否也可以用 GPU 进行通用计算呢？

答案是，能！

由于这里涉及很多跨领域知识，为了让所有前端er 们能深入的理解其来龙去脉，下面做一些周边知识铺垫。

CPU VS GPU

为什么要 GPU 来提供计算加速 ? CPU 不行吗？

解释这个问题，要从这两种芯片的设计定位说起，如下图

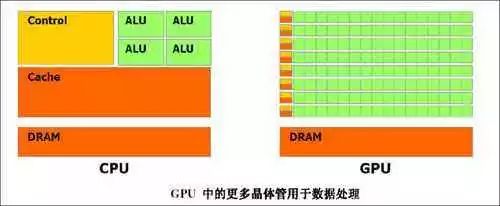
通过 GPU 加速浏览器浮点数计算能力

上图绿色方块即是算术运算单元(ALU)，可以看出就单个 ALU 单元来讲，CPU 比 GPU 要强大很多，频率也高出很多（普遍在 1.2 - 4 Hz）。但为什么总体计算力却相差很多呢？关键问题在于数量与排布。

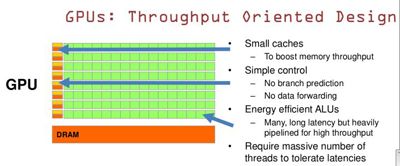
简单来说，计算能力只是 CPU 的众多能力之一，除此之外 CPU 还要随时处理读取、中断、译码、转址等多种繁杂工作。自 1989 年 i486 首次采用流水线概念后，CPU 的利于效率被大幅提升，但受限于任务种类庞杂，过长的流水线必然会导致这条流水线上总有几个执行单元处于闲置状态， Intel 公司用了数年的时间来平衡这一设计。

GPU 面临的情况则不同，3D 空间顶点变换是一种类型完全相同的计算，只不过数量较大而已，完全可以打造出多条与任务匹配的 “临时流水线” 并行工作，分担这些工作。

通过 GPU 加速浏览器浮点数计算能力

就像上面，当茶壶的视角发生变化，其 MV 矩阵（模型视图矩阵）也会变化，重新计算 MV 矩阵并不费力，费力的是要将新矩阵应用到茶壶的每一个顶点。所以像更新矩阵这种 “高技术含量” 的工作一般由 CPU 来负责，而对每一个顶点执行结果这种 “体力活” 由 GPU 负责。总的来讲 GPU 更适合处理大批量的简单任务，而 CPU 趋向的是一种全能型设计。两者分工不同，相互辅佐。

GLSL

GLSL 是一种可编程着色器语言，通过它，我们可以将大量的 GPU 计算单元组成临时的流水线。 GLSL 原生支持向量、矩阵计算，可以方便的在编程中完成空间变形。 WebGL 中也需要用到 GLSL ，源码一般存在 JS 文件中，使用时被编译成着色器对象。受篇幅限制，关于更多 GLSL 的信息在扩展阅读 GLSL-Card中文手册

下面介绍如何在浏览器端使用 WebGL 进行通用计算：

Step 1. 编写 GLSL 版的计算程序

浏览器环境中，所有在 JS 中进行的计算统统会在 CPU 中进行。所以我们需要编写一版功能相同的 GLSL 代码，代替 JS 的工作。

举个例子：计算 0.123456789 的平方。

JS 版本:

GLSL 版本:

接着，创建 canvas 对象，这里要注意画布的尺寸不能太大（256x256），因为 WebGL 中坐标系的边界为 -1 ， 1 。尺寸太大的 canvas 可能会在 gl 光栅化时坐标精度不够发生错位,无法准确的选到指定数据对应的那个像素。

通过 WebGL 提供的 API 将 attribute 变量 a_somefloat 送入 GLSL 。

如何使用 webGL API 并不是本文讨论的重点，涉及到的部分作用领会即可。总之，上面的目的是将包含 0.123456789 这个 float 数的 bufferObject 发送至 GLSL。

注：js 中的 number 是 64bit double ，目前 GLSL 一般最高只支持到 32位浮点数精度，这里会有一些精度流失

Step 2. GLSL 分割计算结果

由于 WebGL 并不提供数据输出接口，所以我们要把计算后的数据转换成 8bit * 4 的 RGBA 颜色形式。这么做虽然有点无奈，不过方法可行。

举例来说，要把 0.123456789 转换成 8bit * 4 的形式方法如下：

确定 R：

确定 G:

确定 B:

确定 A:

结果：

RGBA = (31,154,221,55)，转换为 0-1 范围为：

示意图：

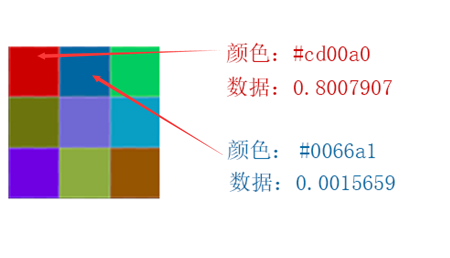
通过 GPU 加速浏览器浮点数计算能力

当然，这是一种比较理想的状况，如果浮点数的整数位有值得话，很可能还需要再分出 8 bit 来用于表示整数，这样会导致只有 3 字节的体积来表示尾数，计算精度会遭到损失。

最后将 RGBA 数据绘制在 canvas 的指定位置上。

Step 3. JS 还原数据

JS 读取 canvas 上面的像素颜色，并将其进行还原。

可以看出 0.123456789 - 0.12345678894780576 = 5.21942350450999e-11 ，造成精度差异的原因有两个，

1.GLSL 本身支持精度限（GLSL 非 IEEE 754 浮点数标准）。

2.将结果转换为 8bit * 4 RGBA 形式时产生的精度差异（最大精度 2^-16）。

总结

这是一种剑走偏锋的方法，虽然实现了最终结果，但精度误差使我们不得不从新考量它的实用性。在 github 上已经有在此方法理论上做出工具库 webglcl 、 gpu.js ，笔者跑了它提供的 benchmarks demo ，性能约为纯 CPU 计算的 10-30 倍之间。相信如果任务数再扩大一些，这个分数差距很可能会更大。

通过 GPU 加速浏览器浮点数计算能力