转载

如何使用变分自编码器VAE生成动漫人物形象

以上是通过变分自编码器生成的动画图片样本。想要获得本文在 Github 代码仓库中的相关代码请点击：https://github.com/wuga214/IMPLEMENTATION_Variational-Auto-Encoder

在图像生成领域，人们总是喜欢试着将变分自编码器（VAE）和对抗生成网络（GAN）相比较。人们的共识是，VAE 更容易被训练，并且具有显式的分布假设（高斯分布）用于显式的表示和观察，而 GAN 则能够更好地捕获观测值的分布并且对观测分布没有任何的假设。结果就是，每个人都相信只有 GAN 能够创造出清晰而生动的图片。虽然可能确实是这样，因为从理论上讲，GAN 捕获到了像素之间的相关性，但是没有多少人试过用比 28*28 维的 MNIST 数据更大的图片作为输入训练 VAE 来证明这一点。

在 MNIST 数据集上有太多变分自编码器（VAE）的实现，但是很少有人在其他的数据集上做些不一样的事情。这是因为最原始的变分自编码器的论文仅仅只用 MNIST 数据集作为了一个例子吗？

流言终结者！

现在，让我们做一个「流言终结者」的实践来看看 VAE 图像生成器的效果是多么不尽人意。例如，下面这些图像。

如何使用变分自编码器VAE生成动漫人物形象

模糊不清的 VAE 样例。

我们从寻找一些 GAN 的对比组开始。我在 Google 上搜索了」GAN 应用程序」，并且发现了一个非常有趣的 Github 代码仓库，这个代码仓库总结了一些 GAN 应用程序：https://github.com/nashory/gans-awesome-applications

为什么「GAN 应用程序」就可以呢？好吧，很难找到不是图像生成的 GAN 应用程序，不是吗？为了让这个实践更加令人兴奋，我们这次将尝试用生成模型输出一些动漫形象！

首先，让我们看看一个 GAN 模型完成这个任务的效果有多好。下面的两组图片来自于两个做动漫图片生成的项目，它们被很多人选择并且以此为基础开展工作：

1）https://github.com/jayleicn/animeGAN

2）https://github.com/tdrussell/IllustrationGAN

如何使用变分自编码器VAE生成动漫人物形象

还不错哦，不是吗？我喜欢它们的色彩，它们和真实的图片十分相似。

如何使用变分自编码器VAE生成动漫人物形象

尽管这些图片里面有些重影，但它们看上去更好。我猜窍门是放大图像，仅仅只看人脸。

结果表明，GAN 的优异表现令人印象深刻。这让我倍感压力。

额... 我们还应该继续吗...

从哪里获得数据？

很不幸，在网络上没有可以得到的标准动漫形象数据集。但是这不能阻止像我这样的人去寻找它。在浏览了一些 GitHub 代码仓库之后，我得到了一些提示：

一个叫做「Getchu」的日本网站有大量的动漫图片。
需要一些工具从网上下载图片，但是你需要自己找到这种工具。（我在这里向你提供一个可能是不合法的）
有很多预训练好的 U-net/ RCNN 动漫人脸检测器，比如 lbpcascade_animeface，这样一来你就可以将人脸提取成 64×64 的图片。

变分自编码器 VAE

本文假设你已经阅读了大量关于变分自编码器的帖子。如果你没有的话，我想向你推荐下面这几篇文章：

Intuitively Understanding Variational Autoencoders (https://towardsdatascience.com/intuitively-understanding-variational-autoencoders-1bfe67eb5daf)
Tutorial—What is a variational autoencoder? (https://jaan.io/what-is-variational-autoencoder-vae-tutorial/)
Introducing Variational Autoencoders (in Prose and Code) (http://blog.fastforwardlabs.com/2016/08/12/introducing-variational-autoencoders-in-prose-and.html)
在 TensorFlow 中对比两大生成模型：VAE 与 GAN

所以，在你知道了什么是 VAE 以及如何实现它之后，现在的问题就是「如果知道目标函数和实现方法就足够去训练一个变分自编码器了吗？」我认为答案是肯定的，但是它并不想通常说的那么简单。例如，这个目标函数来自哪里的问题，以及 KL 散度分量在这里有什么作用。在这篇帖子中，我会试着去解释 VAE 背后隐藏的奥秘。

变分推断是一种在概率图模型（PGM）中推断复杂分布的技术。直观地说，如果你不能很容易地捕获复杂分布的最优点，你就可以用一些像高斯分布这样的简单分布来近似估计它的上界或者下界。例如，下图展示了如何使用高斯分布近似估计局部最优解。

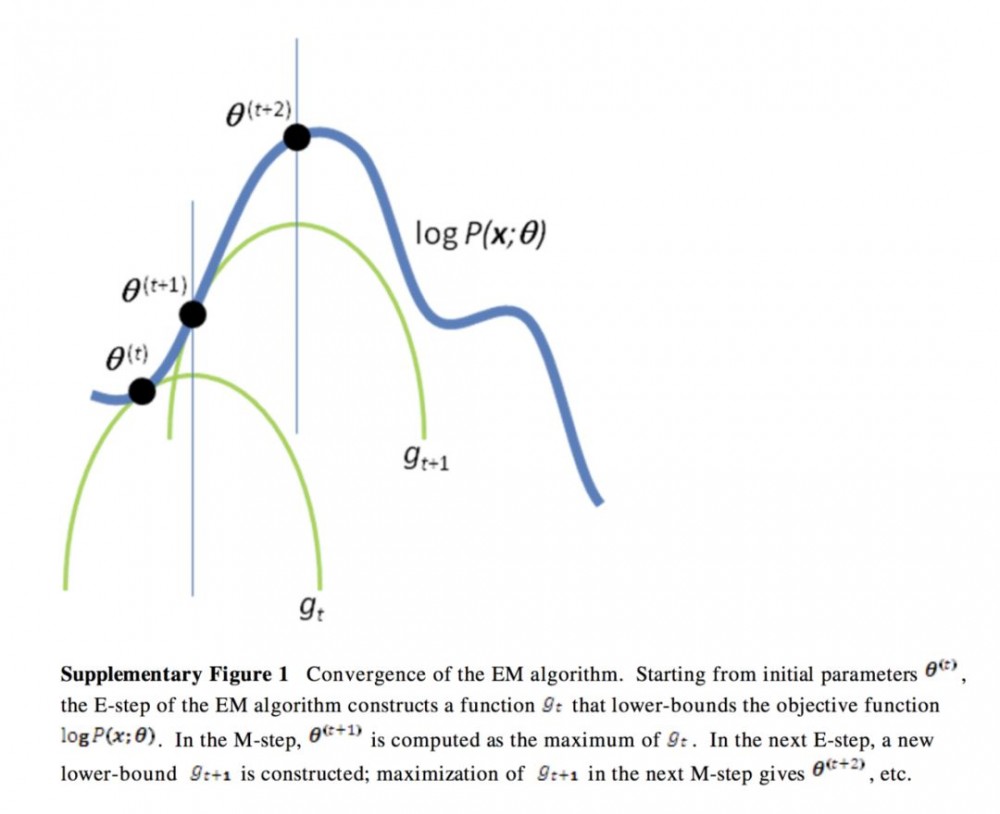
如何使用变分自编码器VAE生成动漫人物形象

图片来自：https://people.duke.edu/~ccc14/sta-663/EMAlgorithm.html

请忽略标题中的 EM（最大期望算法）。这是一个在概率图模型中经典的优化方法，它能够更新变分下界，但是现在你在深度学习中会使用随机梯度下降算法（SGD）。

KL 散度是另外一个在概率图模型中会用到的非常重要的技术。它用来测量两个分布之间的差异。它不是一个距离度量，因为 KL[Q||P] 不等于 KL[P||Q]。下面的幻灯片展示了这种差异。

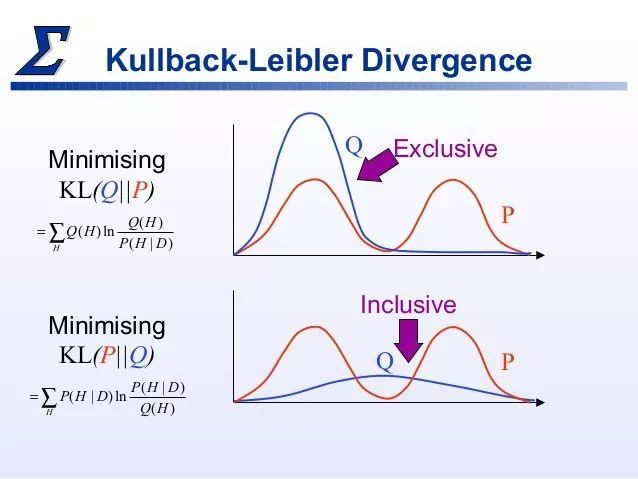
如何使用变分自编码器VAE生成动漫人物形象

图片来自： https://www.slideshare.net/Sabhaology/variational-inference

显然，在 Q>0 时，KL[Q||P] 不允许 P=0. 换句话说，当最小化 KL[Q||P] 时，你想用 Q 分布来捕获 P 分布的一些模式，但是你必然会忽略一些模式的风险。并且，在 P>0 时，KL[P||Q] 不允许 Q=0。换句话说，当最小化 KL[P||Q] 时，你想让 Q 捕获整个分布，而且如果有需要的话，完全忽略掉 P 的模式。

到目前为止，我们直观地明白了两个事实：

「变分」大致是对上界或者下界的近似。
「KL」衡量两个分部之间的差异。

现在让我们回过头来看看 VAE 的目标函数是怎么得来的。

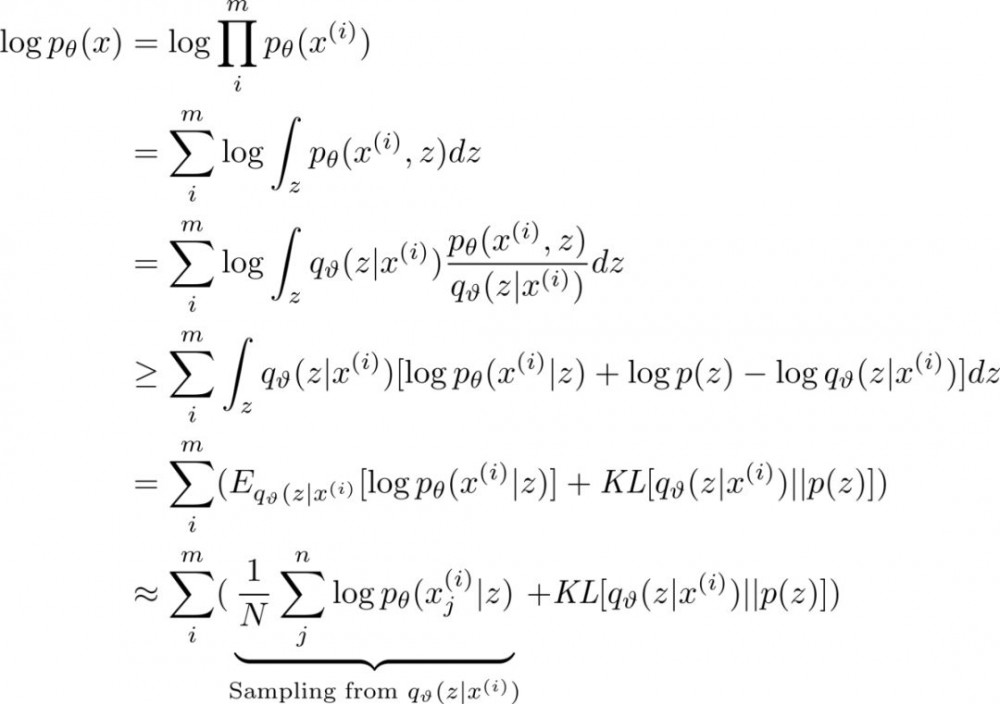
如何使用变分自编码器VAE生成动漫人物形象

这是我对 VAE 的推导。尽管它似乎与你可能在论文中看到的看起来不同，但这是我认为最容易理解的推导。

给定一些图像作为训练数据，我们想要拟合一些能够尽可能准确地表示训练数据的参数（theta）。正式一点说，我们想要拟合用于最大化观测值的联合概率的模型。因此，你会得到左边的表达式。

「z」从何而来？

z 是创造观测值（图像）的潜在表示。直观地说，我们假设一些神秘的画家在数据集中创作这些图像（x），我们将它们称作 Z。并且，我们发现 Z 是不确定的，有时 1 号画家创作了图片，有时候是 2 号画家创作了图片。我们仅仅知道所有的艺术家都对他们所画的图片有着特别的偏爱。

大于等于号是怎么来的？

Jensen 不等式如下所示。注意: log 是凹函数，所以在我们的例子中，不等式反过来的。

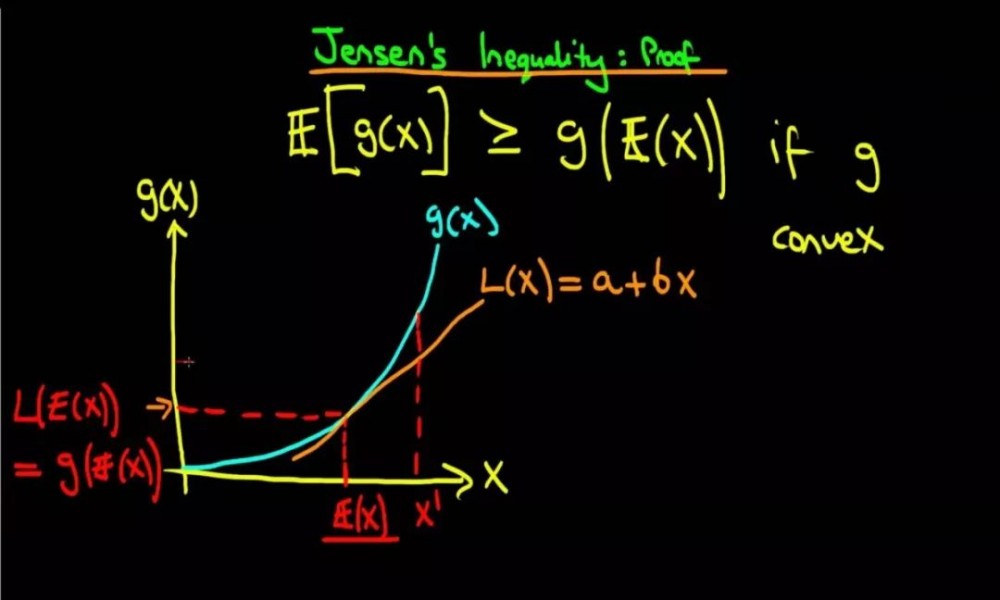
如何使用变分自编码器VAE生成动漫人物形象

图片来自 Youtube：https://www.youtube.com/watch?v=10xgmpG_uTs

为什么在最后一行取近似？

我们不能对无穷的可能的 z 做几分，所以我们使用数值逼近，这意味着我们从分布中进行抽样来对期望取近似。

什么是 P(x|z) 分布？

在变分自编码器中，我们假设它是高斯函数。这就是为什么在优化 VAE 时，要做均方误差（MSE）。

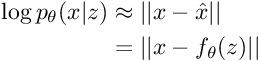
如何使用变分自编码器VAE生成动漫人物形象

f 函数是解码器！哦！在范数之后应该有平方符号。

@staticmethod
def _gaussian_log_likelihood(targets, mean, std):
    se = 0.5 * tf.reduce_sum(tf.square(targets - mean)) / (2*tf.square(std)) + tf.log(std)
    return se
@staticmethod
def _bernoulli_log_likelihood(targets, outputs, eps=1e-8):
    log_like = -tf.reduce_sum(targets * tf.log(outputs + eps)
                              + (1. - targets) * tf.log((1. - outputs) + eps))
    return log_like

P(x|z) 的假设: 高斯和伯努利分布。代码显示了负的对数似然，因为我们总是希望最小化错误，而不是在深度学习中显式地最大化似然。

你在 Github 中看到如此多的 softmax 函数的原因是，对于像 MNIST 这样的二进制图像，我们假设分布是伯努利分布。

什么是 P(z|x) 分布？

这是高斯分布。这就是为什么你看到 KL 散度的实现是一个近似的解。不明白吗？不要担心，你可以看看这篇里：https://stats.stackexchange.com/questions/318184/kl-loss-with-a-unit-gaussian

@staticmethod
def _kl_diagnormal_stdnormal(mu, log_var):
    var = tf.exp(log_var)
    kl = 0.5 * tf.reduce_sum(tf.square(mu) + var - 1. - log_var)
    return kl

Python 语言编写的 KL 散度近似形式的表达式

这个等式怎么能成为一个自编码器呢？

等式中有两类参数。参数 theta 是用来对分布 P(x|z) 建模的，它将 z 解码为图像 x。变体的 theta 是用来对分布 Q(z|x) 建模的，它将 x 编码成潜在的表示 z。

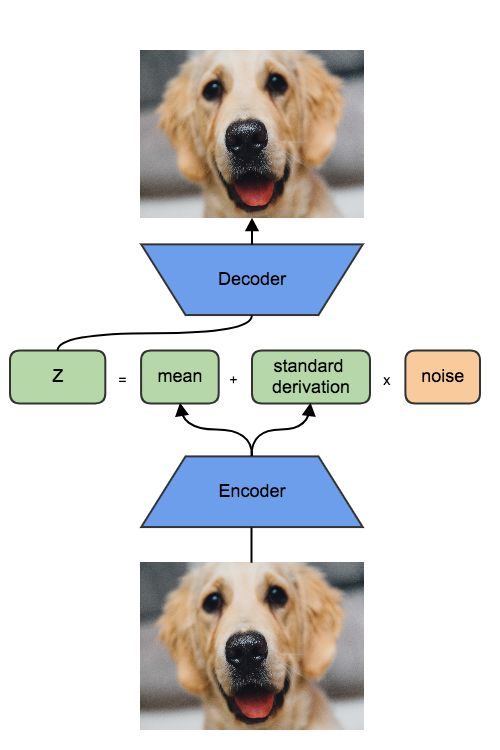
如何使用变分自编码器VAE生成动漫人物形象

自制的变分自编码器的示意图。绿色和蓝色的部分是可微的，琥珀色的部分代表不可微的白噪声。每个人都用著名的猫的图片，所以这里我使用了狗。我不知道我从哪里得到的这张可爱的狗狗图片。如果你知道，请告诉我，这样我可以正确地引用原始网站。

相应的 TensorFlow 计算图谱：

def _build_graph(self):
    with tf.variable_scope('vae'):
        self.x = tf.placeholder(tf.float32, shape=[None, self._observation_dim])
        with tf.variable_scope('encoder'):
            encoded = self._encode(self.x, self._latent_dim)
        with tf.variable_scope('latent'):
            self.mean = encoded[:, :self._latent_dim]
            logvar = encoded[:, self._latent_dim:]
            stddev = tf.sqrt(tf.exp(logvar))
            epsilon = tf.random_normal([self._batch_size, self._latent_dim])
            # Reparameterization Trick
            self.z = self.mean + stddev * epsilon
        with tf.variable_scope('decoder'):
            decoded = self._decode(self.z, self._observation_dim)
            self.obs_mean = decoded
            if self._observation_distribution == 'Gaussian':
                obs_epsilon = tf.random_normal([self._batch_size, 
                                                self._observation_dim])
                self.sample = self.obs_mean + self._observation_std * obs_epsilon
            else:
                self.sample = Bernoulli(probs=self.obs_mean).sample()

VAE 目标函数的两个组成部分的意义

最小化 KL 项：将 P(z|x) 看作 N(0,1)（标准正态分布）。我们希望通过从标准正态分布中抽样来生成图像。因此，我们最好让潜在的分布尽可能地接近标准正态分布。
最大限度地减小重构损失：创造尽可能生动/真实的图像。最小化真实的图像和生成的图像之间的误差。

很容易看到，为了使 VAE 很好的工作，平衡这两个部分是十分关键的。

如果我们完全忽略 KL 项，变分自编码器将收敛到标准的自编码器，它将删除目标函数中的随机部分。因此，VAE 不能生成新的图像，只能记住并且展示训练数据（或者创造纯粹的噪声，因为在那个潜在的位置没有编码的图像！）如果你足够幸运的话，理想的结果是实现了核主成分分析！

如果我们完全忽略了重构项，那么潜在的分布会退化成标准的正态分布。所以无论输入是什么，你总是得到类似的输出。

如何使用变分自编码器VAE生成动漫人物形象

一个 GAN 退化的案例。VAE 的情况也相同。图片来自：http://yusuke-ujitoko.hatenablog.com/entry/2017/05/30/011900

现在我们明白了：

我们希望 VAE 生成合理的图像，但是我们不想让它显示训练数据。
我们想从标准正态分布中取样，但是我们不想一次又一次地看到同样的图像。我们希望模型能产生差别非常大的图像。

那么，我们如何平衡它们呢？我们将观测值的标准差设置成一个超参数。

with tf.variable_scope('loss'):
    with tf.variable_scope('kl-divergence'):
        kl = self._kl_diagnormal_stdnormal(self.mean, logvar)
    if self._observation_distribution == 'Gaussian':
        with tf.variable_scope('gaussian'):
            # self._observation_std is hyper parameter
            reconst = self._gaussian_log_likelihood(self.x, 
                                                    self.obs_mean, 
                                                    self._observation_std)
    else:
        with tf.variable_scope('bernoulli'):
            reconst = self._bernoulli_log_likelihood(self.x, self.obs_mean)
    self._loss = (kl + reconst) / self._batch_size

我看到人们经常将 KL 项设定为一个像 0.001×KL + Reconstruction_Loss 这样的值，这是不正确的！顺便问一下，这就是很多人只在 MNIST 数据集上做 VAE 的原因吗？

还有什么值得注意的呢？模型的复杂程度是支撑损失函数的关键因素。如果解码器太复杂，那么即使是较弱的损失也不能阻止它过拟合。结果是，潜在的分布被忽略了。如果解码器太简单了，模型就不能合理地解码潜在的表示，最终只能捕获一些粗略的轮廓，就像我们之前所展示的图像那样。

最后，如果我们上面做的事情都是正确的，是时候看看 VAE 的力量了。

如何使用变分自编码器VAE生成动漫人物形象