新加坡国立大学论文:利用互补几何模型改善运动分割
许多几何模型被用于运动分割问题,模拟不同种类的相机、场景以及运动。通常情况下,这类问题的基本模型通常是被认为适用于不同场景的,而这些场景是互不重叠的。例如,当这个基础的运动是一种普通的运动时,人们一般使用基础矩阵来模拟对极几何 [16 , 23];而当场景里的运动退化成为平面内的运动或者一个纯旋转时,人们则通常选择单应性矩阵 [6 , 18]。然而,事实上,现实世界场景里的动作不是那么好划分的:它们可以是一个近似退化的场景,例如一个几乎却不完全是平面的场景,或者一个以旋转为主的运动同时兼有非零平移的运动。在这样的情景下,选用模型时如果采用了错误的分类,会给后续的子空间划分造成困难。
举个例子,众所周知,在具有主平面的场景中找到属于退化结构(主平面)的内点是简单的,但是可能导致基础矩阵的精确度非常低。大部分处于退化结构之外的内点会丢失,并且在很多情况下, 这种有错误的基础矩阵会选取异常值(例如:从其他动作组当中选取点)。由于这并不是一个单纯的平面场景,单纯地使用单应性矩阵也可能无法将所有的内点组合到一起,导致子空间的过度分割。
从运动分割相关文献的角度来看,对于许多模型来说,由于缺少 Hopkins155 基准 [31] 中提及的透视效应,通常都会回避使用基础矩阵。然而,这种方法中的退化导致的数值难题是否无法解决仍是未知的。并且,也没有人研究过其中得到的亲和矩阵(affinity matrix)到底是如何不适用于子空间划分的:仅仅由于退化还是存在别的影响因素?考虑现实生活中的许多应用(例如自动驾驶),在这些应用里透视效应是十分常见的,因此我们应该对基础矩阵(或单应性矩阵)用作运动分割模型的适应性有更深的了解。
事实上,研究者认为,事情不只是这么简单。举个例子,如果我们对宽视野场景运用基础矩阵,如同 KITTI 基准 [9] 中提到的一样,会比运用单应性矩阵得到更好的结果吗?我们暂时还没有理由相信结果将会是这种情况,因为通过比较,基于仿射模型的许多算法仍然能胜过那些基于拥有更大视野的单个 Hopkins 序列中基础矩阵的算法(尽管公认差不多)。其实,从用于测试现实世界场景中运动分割的 KITTI 序列得到的结果来看,其再次体现了基于单应性方法的优点。自然而然地,有人就会问,除了退化之外,是什么因素对基础矩阵方法产生了不好的影响?而且为什么单应性矩阵方法在处理广视角场景时能保持它自己的特点?什么时候它才会失去基础矩阵的几何精确性?
在这章节的余下部分里,我们将会简要的探讨单应性矩阵(H)和基础矩阵(F)作为几何模型应用于运动分割的适应性。之后我们将会将 H 和 F 的亲和矩阵相应地表示为 KH 和 KF。
H 的成功原因
前面的段落已经提及了亲和矩阵 KH 可能没有很高的集群内聚力的事实(由于相同刚体运动的不同平面间缺乏强的亲和性),所以可能导致人们对其是否适用运动分割任务表示怀疑。在 Hopkins155 数据集中,这并不是最重要的问题,因为大部分的场景拥有小的视野,并且场景足够遥远以至于可以被近似于一个平面;由于基于仿射子空间或单应性矩阵的各种方法得到的良好结果,这些近似被证明行之有效。最近的基于单应性的方法 [18] 称得到了目前最好的实验结果,平均误差为 0.83%。考虑到实际存在的一些有不可忽略透视效应的 Hopkins 序列,这个低误差的结果是值得关注的;同时,相比已经提出的一些原因,这种现象应该还有更好的解释。
上述成功可以归因为由单应性假设过程产生的许多平面切片;这些切片并不一定是场景中的真实物理平面(例如 图 1(a-b) 中的切片),但只要这些虚拟的平面属于同一个刚体运动,它们显然是可用单应性矩阵拟合的。这些场景的切片在多个真实平面的点之间建立了强大的关联,并得到了一个相对更少过度切割的亲和矩阵 KH。如果场景中只包含紧凑的物体或者分段光滑的结构,那么这种关联足以将一个刚性运动的各个表面绑定在一起。然而,在现实世界场景中,当上述情况不能满足的时候,我们怀疑这种关联可能不合适。图 1(c) 展示了一个包含了细长物体(红绿灯)和道路标志的背景。显而易见,在这个场景下,当像往常一样构造虚拟的平面切片时,得到的关联性相比之前提到的是要小的多(大部分的切片不能同时地将这两种元素的大分割块连接起来,不像图 1(a-b) 中的那样)。
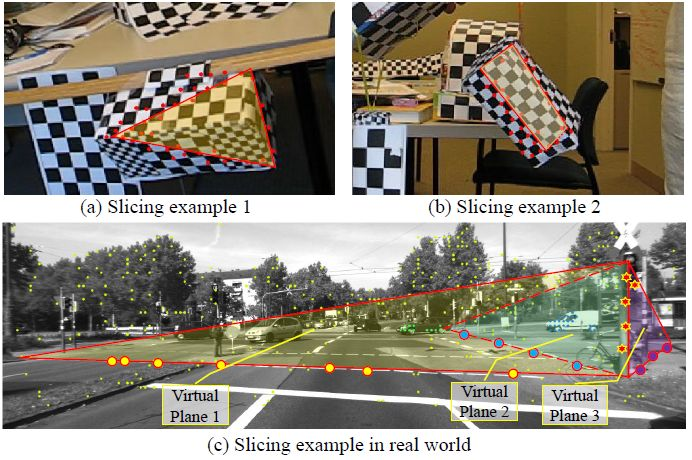 图 1:单应性变换的切片效果图。(a-b) 红色的点表示假设的内点。所有的点都分布在一个用黄色标示的虚拟平面上(立方体的一个切片)。(c) 虚拟的平面用三角形以及同色的内点标示。
图 1:单应性变换的切片效果图。(a-b) 红色的点表示假设的内点。所有的点都分布在一个用黄色标示的虚拟平面上(立方体的一个切片)。(c) 虚拟的平面用三角形以及同色的内点标示。
F 的问题
除了相关文献提及的经典结构中已为人熟知的退化问题之外,研究者认为用于运动分割问题的基础矩阵方法还有一个问题,那就是这个模型实际上是一个囊括了各种情况的模型,它包括了所有类型的场景运动情况。这种复杂模型为后面的聚类以及模型选择任务带来的风险是显而易见的。该模型过于丰富的特征集合使其很容易的捕捉到不同刚体运动之间的任何关联性。因此,相比较为简单的模型,例如单应性变换,它更容易导致不同刚体运动的子空间重叠。然而,这里还有一些其他的问题。作为一个几何上正确的模型(单应性模型很难与之相比),F 是不是提供了为找到最佳视野的最大范围呢?那么 F 应该捕捉多少正确信息呢?我们可能需要在正确的方向上作一些微调,来恢复 KF 应有的表现。从这个角度来看,即使处理一个没有退化的普通场景时,我们仍然有一个继续使用单应性模型的重要理由——得到之前没能得出的 KF。
推荐的解决方案
很不幸的是,我们不得不承认,很多现实世界场景不能被归入一个刚好吻合的类中,例如一个普通的或是退化的场景运动,因此不能通过诸如 H 或 F 之类的任何单一模型来完美解决。本文还讨论了基本矩阵方法的一些缺陷,并且推测尽管得到的 KF 可能不符合任何已有定义的聚类,但是如果我们巧妙地利用来自诸如 H 这类较简单模型的信息,KF 的全部潜力或许会被挖掘出来。考虑到这些,研究者提出了结合上述多种模型的多视角光谱聚类框架。由于还没有确定的关于这类模型性能的指标,作者评估了一些现有的结合性的方案。通过评估,其结果保证了该研究不是特定结合性方案的特例。就像之后将要展示的那样,通过使用改进的 KF,基础矩阵方法的表现将会有显著的提升。当然,我们不应该夸大这种基本矩阵方法的潜在价值。当场景包含了大量的退化的时候,比如真实世界场景,使用结合多视角的方法更容易得到最好的结果。也就是说,我们应当寻找同时考虑了改进的 KF 和改进的 KH 的共同光谱嵌入。
总而言之,本文贡献如下:首先,本文讨论了单应性矩阵和基础矩阵作为运动分割问题几何模型的一些优缺点。然后作者提出了使用亲和矩阵的融合作为处理现实世界效应的手段,而这些效应通常难以用纯粹的单应性或者基础矩阵建模。最后,作者对现有的运动分割数据进行了广泛的测试,基于这些数据该模型获得了当前最好的实验效果;作者还提出了一个改编自 KITTI 基准的更加现实和具有挑战性的数据集,它包括现实世界的一些效应例如强烈透视和强前向平移,这些都是传统数据集所没有的。
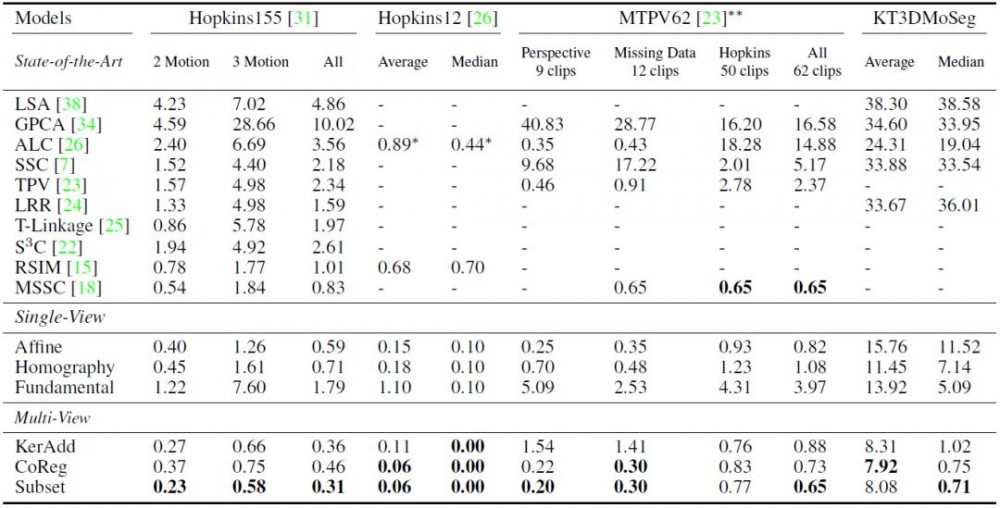
表 1:Hopkins155、Hopkins12、MTPV62 以及 KT3DMoSeg 数据集的运动分割分类误差(%)结果。∗表现最好的模型(RPCA+ALC5 是和 ALC[26] 对应的)。∗∗性能最佳模型的表现和拥有正确动作数量的序列相对应。『−』 意味着还没有测试数据或者没有可使用的开源代码。
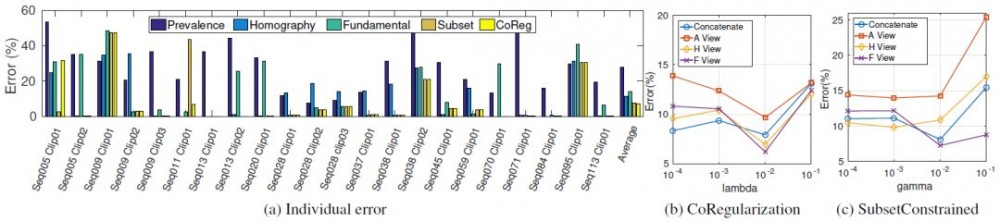
图 2:独立序列分类误差以及 KT3DMoSeg 基准对参数的敏感性。

图 3:KT3DMoSeg 场景序列的运动分割举例
论文:Motion Segmentation by Exploiting Complementary Geometric Models(利用互补几何模型的运动分割)

论文地址: https://arxiv.org/abs/1804.02142
许多现实世界的场景不能简单的被归类为普通的或者退化的;在这种情况之下,在处理运动分割问题按二分法选择利用基础矩阵或者单应性矩阵时,错误的选择会造成困难。即使是处理一般的运动场景,使用基础矩阵方法作为模型来处理运动分割问题仍然有其弊端,这些我们在文中都提到了。基础矩阵方法的全部潜力只有当我们小心地利用较为简单的单应性模型的信息时才能实现。考虑到这些,我们提出了一个结合了多种模型的多视角光谱聚类的框架。通过对现有的运动分割数据进行了广泛的测试,我们获得了最好的实验结果;我们还提出了一个改编自 KITTI 基准的更加现实和具有挑战性的数据集,它包括了现实世界的一些效应例如强烈透视和强前向平移,这些都是传统数据集所没有的。











![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)

