转载

TensorFlow入门：线性回归

TensorFlow也是很多程序员耳熟能详的机器学习框架了，于2014年开源并且有着活跃的社区，前几天TensorFlow开发者大会也宣布了TensorFlow for JS和Swift，借着这个机会来写一写TensorFlow的入门教程和机器学习入门需要用到的一些知识吧。这次从最基本的线性回归开始，这篇文章将会对一个数据集进行线性回归并且计算出来表达式。

问题描述：线性回归（Linear regression）

现行回归的思路并不难，线性回归的核心思路就是将一堆数据使用线性的解析式来表达，也就是一次函数。一次函数是每个人初中就学到的，y = k*x + b，其中k是斜率，b是纵截距。通过这个表达式，给一个x值，都会有一个y值与之对应。在现实生活中的很多现象也可以使用这个模型表现，在这里举一个例子，房屋的大小和价格，假设我们拿到了一组房屋大小和价格的表，并且将它绘制出来。

TensorFlow入门：线性回归

这时可以发现，价格和房屋大小是存在一个线性的关系，通过拟合一条直线就可以推断任何房屋大小的价格。

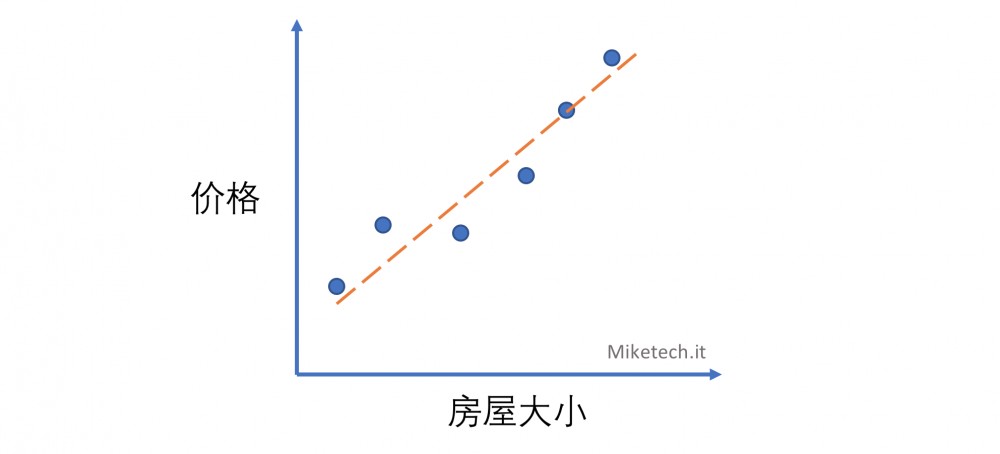
TensorFlow入门：线性回归

根据给出点的坐标，来拟合出一个直线，得到这个直线的解析式就是线性回归需要做的。在这里为了方便理解，我将 y = k*x + b 重新写成 y = w * x + b，w代表权重(weight),b代表偏差(bias)。那么，输入一系列点，程序算出来weight和bias就是这次的目的。

TensorFlow入门：线性回归

数据集读取

首先是数据集的读取，我预先在excel上生成了一些点，第一列代表横坐标，第二列代表纵坐标，从绘制的散点图来看，这一系列点完全程线性分布，那我我将会对这些点进行线性回归。

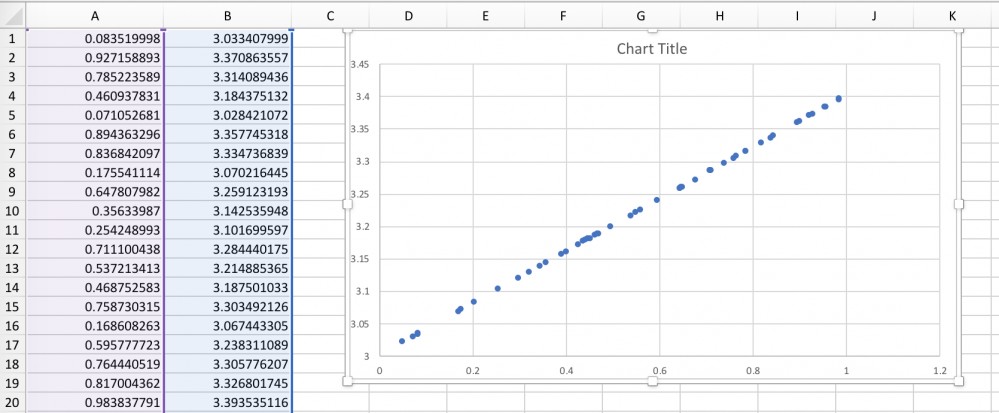
TensorFlow入门：线性回归

首先使用numpy读取这个CSV文件并且将第一列和第二列存到两个数组里

import tensorflow as tf
import numpy as np

my_data = np.genfromtxt('dataset.csv', delimiter=',', dtype=float)
x_data = np.array(my_data[:,0])
y_data = np.array(my_data[:,1])

print(x_data)
print(y_data)

运行程序，x_data和y_data被打印了出来

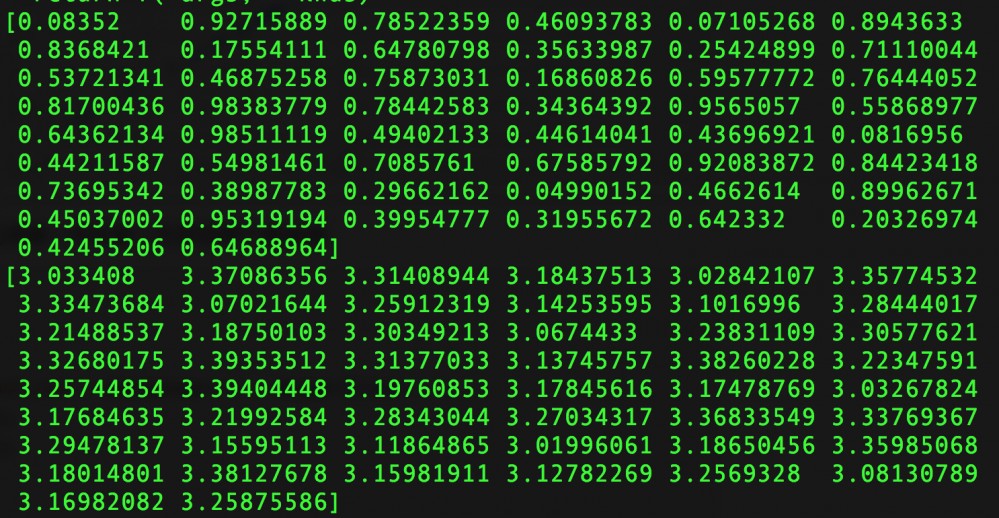
TensorFlow入门：线性回归

模型搭建

接下来就是搭建模型了，这个问题中当然是线性模型啦, 首先声明weights变量是一个 -1到 1值，bias变量默认为0，表达式 y = weights * x_data + biases 就是模型了。

weights = tf.Variable(tf.random_uniform([1], -1,0, 1.0))
biases = tf.Variable(tf.zeros([1]))

y = weights*x_data + biases

计算误差：均方误差（Mean Square Error）

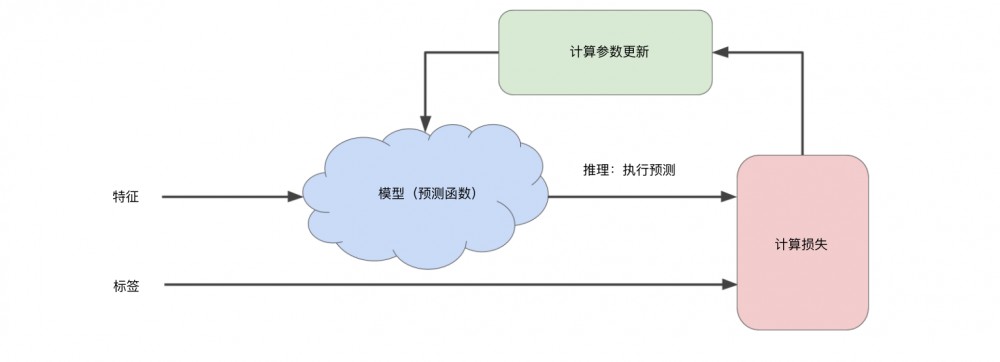
模型规定之后，开始训练之后TensorFlow会不断地生成weight和bias，但是weight和bias千千万，怎样能找到与数据集中的点最为匹配的呢？在下面一组图中，有三条曲线，每一条曲线都有斜率和截距，从图中看，第一条曲线是最匹配这些点的。不过，怎么用数学方法来表示呢？这就要引入平方损失了， 损失是一个数值，代表着对糟糕预测的惩罚 。

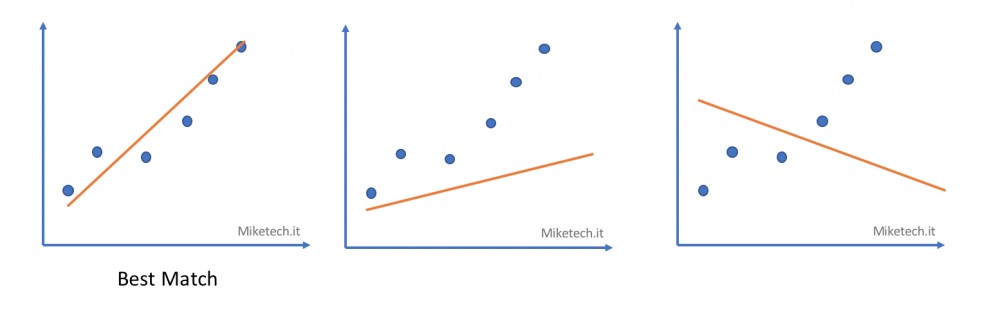
TensorFlow入门：线性回归

在下图中y点就是原坐标( observation )，y‘是预测出来的点( prediction )，红色的箭头就是损失( Loss )

TensorFlow入门：线性回归

平方损失的公式就是 （y – y’）^ 2

更多的时候，会使用 均方误差（MSE） 来计算损失，就是算出来所有样本点的平方误差再取平均数

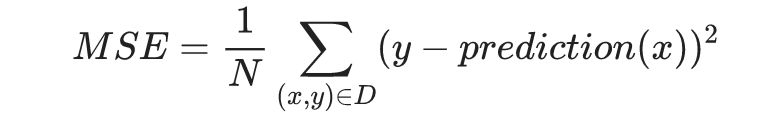
TensorFlow入门：线性回归

在TensorFlow中MSE很好表示

loss = tf.reduce_mean(tf.square(y-y_data))

误差传播：梯度下降法(Gradient Descent)

那么既然算出来了损失，那么总得想办法降低损失吧，在每次迭代的时候，通过传入的损失来对新预测的weight和bias进行调整。这个过程听起来抽象，不过大家都玩过猜价格的游戏吧，你猜一个东西的价格，我回答，“高了”或者“低了”来对你进行反馈，你通过我的反馈来对新猜出的价格进行调整，从而猜出正确的价格，这就是梯度下降法的核心思路。

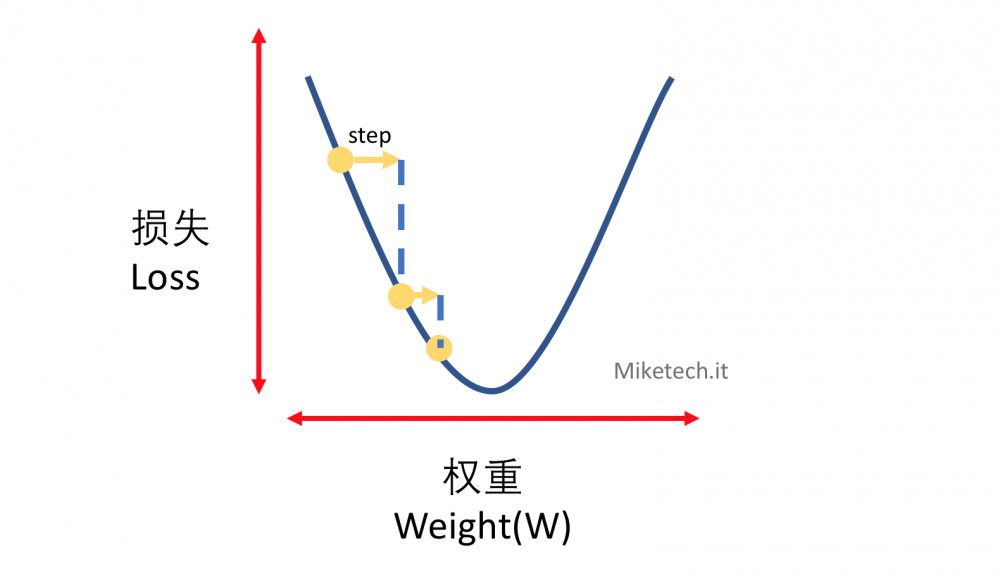
TensorFlow入门：线性回归

来画一个损失和权重的关系图，在所有权重范围（正无穷到负无穷）中，损失和权重的关系程碗型，在最低点的时候损失最小，在损失最小时候的对应权重即为合适的权重。下图从最左边的黄点来计算损失，不停地向右推进，每次推进的大小称之为步长（Step）或者 学习速率 ，直到推进到损失最小的点上。至于是向左推进还是向右推进，这是通过计算函数的偏导数来判断的，感兴趣的同学可以去学习下大学的高等数学。

TensorFlow入门：线性回归

TensorFlow代码实现很容易,下面代码中声明了一个GradientDescentOptimizer，学习速率为0.5

optimizer = tf.train.GradientDescentOptimizer(0.5)

训练

之后就可以开始训练了,首先调用global_variables_initializer()函数初始化所有的tensor变量，然后新建一个Session，然后运行迭代201次，每20词迭代输出一次weight和bias的值。

optimizer = tf.train.GradientDescentOptimizer(0.5)
train = optimizer.minimize(loss)

init = tf.global_variables_initializer() 

sess = tf.Session()
sess.run(init)         

for step in range(201):
    sess.run(train)
    if step % 20 == 0:
        print(step, 'weight: ',sess.run(weights), ' bias: ', sess.run(biases))

运行后可以发现结果是收敛的，weight最终结果大概为0.4，bias最终结果为2.999

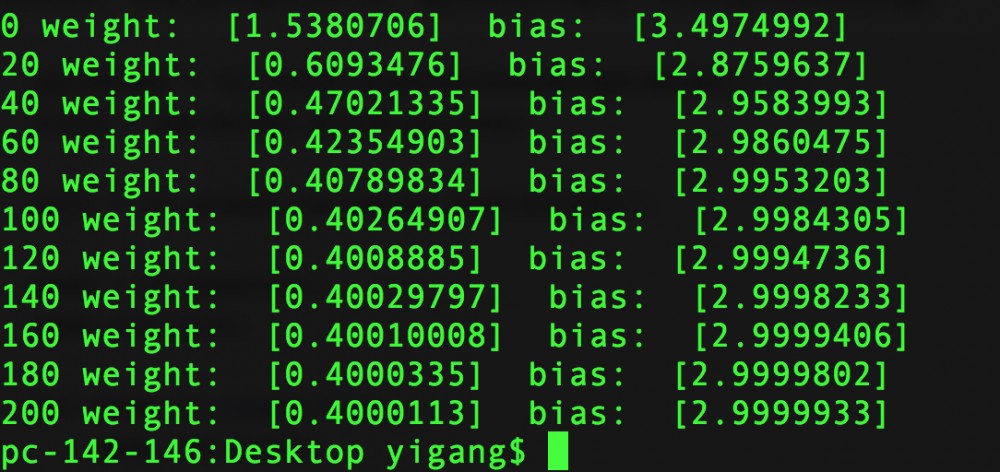
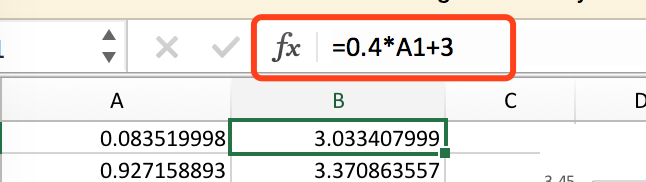
TensorFlow入门：线性回归