转载

跳表的深入浅出——SkipList

跳表作为存储数据结构，在谷歌的数据库开源代码 leveldb 中被广泛使用，当然还有大名鼎鼎的 redis 。跳表的原理相当简单，只要你能熟练操作链表，就能轻松实现一个 SkipList。从而摆脱了红黑树，或者AVL树之类的复杂写法，因为这类数据结构体都要要考虑很多细节，要参考一堆算法与数据结构之类的树，还要参考网上的代码，相当麻烦。跳表是在很多应用中有可能替代平衡树而作为实现方法的一种数据结构。跳跃列表的算法有同平衡树一样的渐进的预期时间边界，并且更简单、更快速和使用更少的空间。

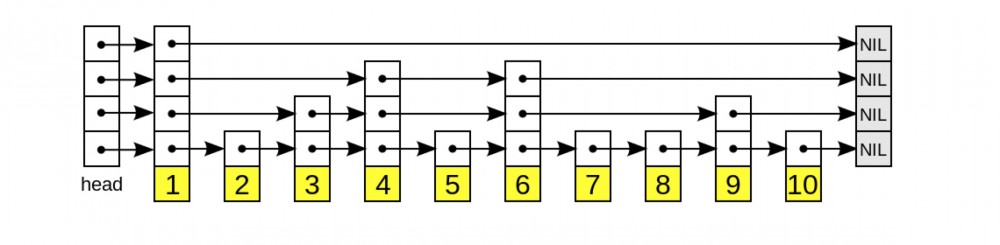
leveldb 存取数据，都在用 MemTable 这个结构体，而 MemTable 核心在于 level::MemTable::Table，也就是 typedef SkipList<const char*, KeyComparator> level::MemTable::Table 。 SkipList 看名字就知道，跳表，是一种数据结构，允许快速查询一个有序连续元素的数据链表。这是一种 “以空间换取时间” 的一种做法，值得注意的是， 这些链表都是有序的 。

跳表的深入浅出——SkipList

关于这个跳表，我查了一下作者(William Pugh)给出的解析:

Skip lists are a data structure that can be used in place of balanced trees. Skip lists use probabilistic balancing rather than strictly enforced balancing and as a result the algorithms for insertion and deletion in skip lists are much simpler and significantly faster than equivalent algorithms for balanced trees.

跳表是平衡树的一种替代的数据结构，但是和红黑树不相同的是，跳表对于树的平衡的实现是基于一种随机化的算法的，这样也就是说跳表的插入和删除的工作是比较简单的。

也就是说核心在于随机算法，一个靠谱的随机算法对跳表是非常重要的。

现在我们来一边用代码加图解来分析一下跳表魅力！

跳表数据存储模型

跳表数据结构如下：

template <typename Key, typename Value>
class SkipList {
private:
	struct Node; // 声明节点结构体
	
public:
  explicit SkipList(); 

private:
  int level_;  // 跳表层数
  Node* head_; // 跳表头部节点列表
  unit32_t rnd_; // 随机数因子
  
  // 生成节点方法
  Node* NewNode(int level, const Key& key,  const Value& value);
 
  Node* FindGreaterOrEqual(const Key& key, Node** prev) const;
  
};

节点数据结构：

template <typename Key, typename Value>
struct SkipList<Key, Value>::Node {

  explicit Node(const Key& k, const Value& v) : key(k), value(v) {}

  Key key;  
  Value value;
  
  void SetNext(int i, Node* x);  
  Node* Next(int i)；
  
private:
  struct Node* forward_[1]; // 节点数组列表，这个比较重要，后面会详细介绍，如果不理解这个变量，就很难理解跳表了
}

通过图来看一下总体结构

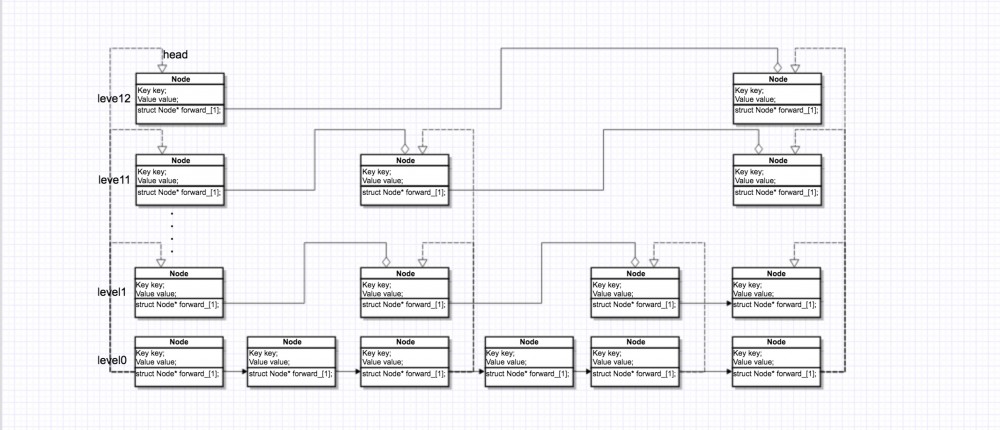
跳表的深入浅出——SkipList

ps:图中虚线链接表述数组关系，实现标识指针链表关系

上图假设 level 为 4 等级的一个跳表图，，forward_ 变量是一个指针数组，一边指向下一个节点(黑色填充箭头)的链表，一边又是这些链表的数组(透明填充箭头)这样的一个数据结构形成了我们需要的一个链表。

后面我们会称为图中竖向(dowm)节点为 节点数组 ，横向(left)的节点为 节点链表

初始化跳表

首先为了实现这个结构，我们来初始化跳表

enum {kMaxLevel = 12}; // 这里初始化默认跳表最大层数高度为12

template <typename Key, typename Value>
SkipList<Key, Value>::SkipList() : head_(NewNode( kMaxLevel, 0, 0)), rnd_(0xdeadbeef)
{
  // 将 head 节点数组全部初始化
  for (int i = 0; i < kMaxLevel; ++i) {
    head_->SetNext(i, nullptr); // 设置第 i 层节点
  }
}

现在我们的结构就实现了下图的样子了

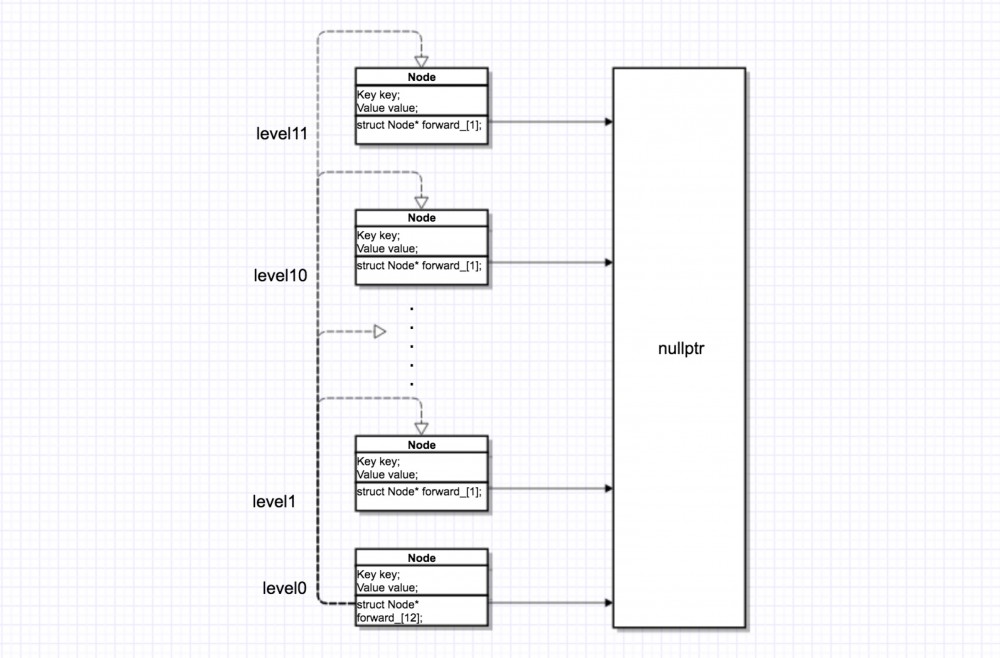
跳表的深入浅出——SkipList

当然，这些节点都是空的就是了。

插入操作

插入操作分为两步：

查找每层链表，知道找到该插入的位置（因为要保持有序的）
更新节点指针和跳表高度

第一步：

template <typename Key, typename Value>
typename SkipList<Key, Value>::Node*
SkipList<Key, Value>::FindGreaterOrEqual(const Key& key, Node** prev) const
{
  Node* x = head_, *next = nullptr;

  int level = level_ - 1;
  
  // 从最高层往下查找需要插入的位置
  // 填充 prev，prev 为用来记录每 层（level）跳点的位置
  for (int i = level; i >= 0 ; --i) {
    while ( (next = x->Next(i)) && next->key < key) {
      x = next;
    }
    if (NULL != prev) {prev[i] = x;}
  }
  return next;  // 返回第 level0 层最合适插入的节点位置
};

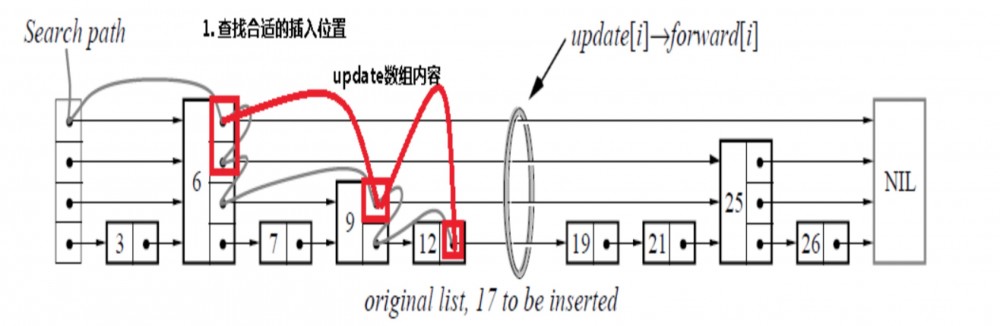
第一步操作如图3.1 所示，往这一跳表中插入 key=17 的操作，可以看出跳表不断寻找跳点，记录跳点 (红色框框住的点，我们以下称为跳点)，寻找该插入的位置，例如图3.1中运行上面代码后，返回了 next 为 key=12 的节点，因为 key=17 大于 12 ，小于 19。

图 3.1

跳表的深入浅出——SkipList

第二步：

template <typename Key, typename Value>
bool SkipList<Key, Value>::Insert(const Key& key, const Value& value) {
  
  /** 第一步实现*/  
  // prev 为用来记录每 层（level）跳点的位置
  Node* prev[kMaxLevel];

  // 查找每层链表，知道找到该插入的位置（因为要保持有序的）
  Node* next = FindGreaterOrEqual(key, prev);
	
  int level;	
  
  // 不能插入相同的key
  if ( next && next->key == key ) {
    return false;
  }
  
  /** 第二部实现， 第二步实现后的代码如图 3.2*/
  // 产生一个随机层数 k
  level = randomLevel();
  if (level > level_) {
    for (int i = level_; i < level; ++i) {
      prev[i] = head_; // 新增的层数初始化
    }
    level_ = level;
  }
  
  // 新建一个待插入节点 next，
  next = NewNode(level, key, value);
  // 逐层更新节点的指针, 一层一层插入
  for (int j = 0; j < level; ++j) {
    next->SetNext(j, prev[j]->Next(j)); // 该节点第 levelJ 层的节点指向 prev （跳点位置）的 levelJ 层链表指向的节点
    prev[j]->SetNext(j, next); // 将 pre 跳点第 levelJ 层链表指向了 Next 第 levelJ 层的链表节点
  }
  
    return true;
}

上述代码中 randomLevel() 生成的层数，就作为了跳表的总层数，同时，也代表了这个新增节点的层数，例如图3.2 中，节点 key=3，高度为1，key=6，高度为4。

图 3.2

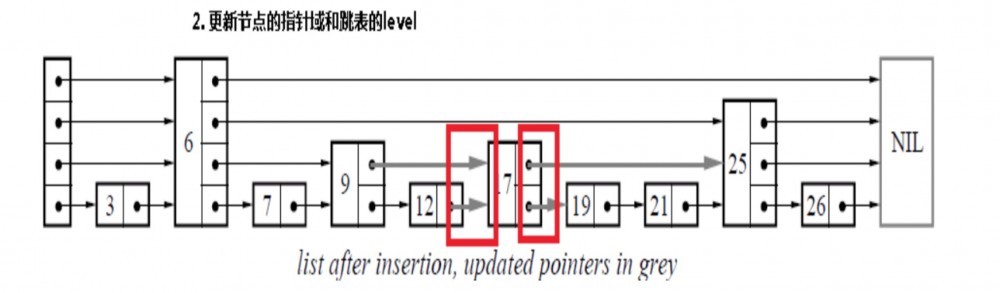
randomLevel 随机层数生成

查找操作

插入操作中的第一步就是我们的查找操作了，就不做解析了，直接封装一层代码

template <typename Key, typename Value>
Value
SkipList<Key, Value>::Find(const Key &key) {
  Node* node = FindGreaterOrEqual(key, NULL);
  if (node) {
    return node->value;
  }
  return NULL;
}

删除操作

在 leveldeb 中，跳表 SkipList 是没有删除操作的，leveldb 的跳表只是用来增加节点个查询节点，如果要删除某个节点，只是将某个节点标记为删除，因为删除操作又得重新计算 level 层数，更新每层的节点链表，这样太耗费性能了。

但是我们在这里还是实现一下跳表的删除操作，同样的，跳表删除和插入操作相同

首先查找到需要删除的节点
如果找到该节点，更新指针域，需要更新 level 的话，逐层更新每个链表

template <typename Key, typename Value>
bool
SkipList<Key, Value>::Delete(const Key&key)
{
  Node* prev[kMaxLevel];
  Node* next = FindGreaterOrEqual(key, prev);

  int level = level_;
  if (next && next->key == key) {
    // 将每层跳点链表设置到 next 节点所指向的每层的链表
    for (int i = 0; i < level; ++i) {
      if (prev[i]->Next(i) && prev[i]->Next(i)->key == next->key) {
        prev[i]->SetNext(i, next->Next(i));
      }
    }

    // 释放该节点数组的所有内存
    free(next);

    //如果删除的是最大层的节点，那么需要重新维护跳表的
    for (int j = level_-1; j >= 0 ; --j) {
      if (head_->Next(j) == NULL) {
        level_--;
      }
    }
    return true;
  }

  return false;
};

图4.1

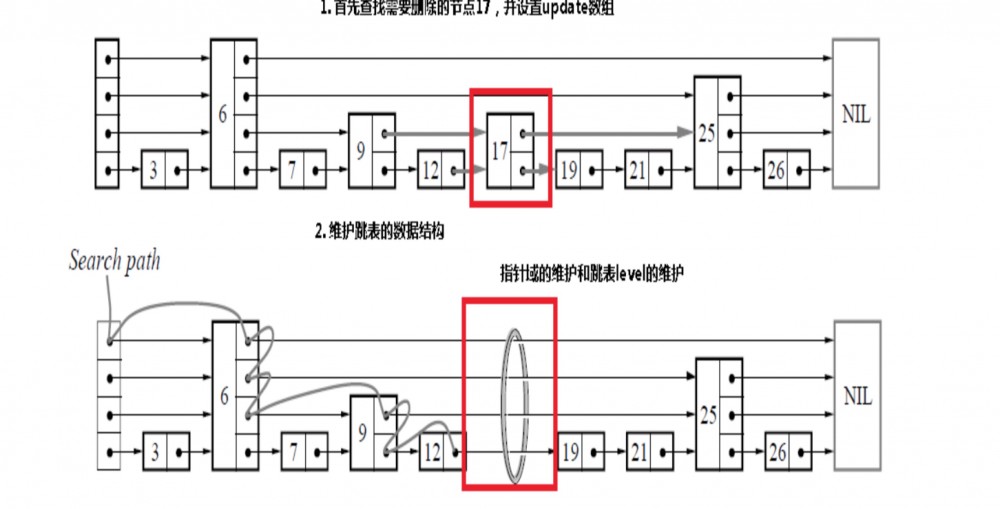
如图4.1所示，删除节点 key=17 时候的操作，先查找并返回 next 节点，检查 next 节点是否 key=17，如果是的是，则将逐层的跳点全部更新过来，并更新层数。

附属实现代码

生成节点方法

template <typename Key, typename Value>
typename SkipList<Key, Value>::Node*
SkipList<Key, Value>::NewNode(int level, const Key& key,  const Value& value)
{
  size_t men = sizeof(Node) + level * sizeof(Node*);
  Node* node = (Node*)malloc(men);
  node->key = key;
  node->value = value;
  return node;
}

代码中 sizeof(Node) 为本身结构体所需要的内存分配，level sizeof(Node ) 是为 forward_ 数组分配内存，因为要配 level 个节点链表。在 leveldb 中使用了字节对齐的方式来分配这块内存，我这边并没有写出来，有兴趣的可以浏览一下源码。

我们假设 level = 4

图 6.1

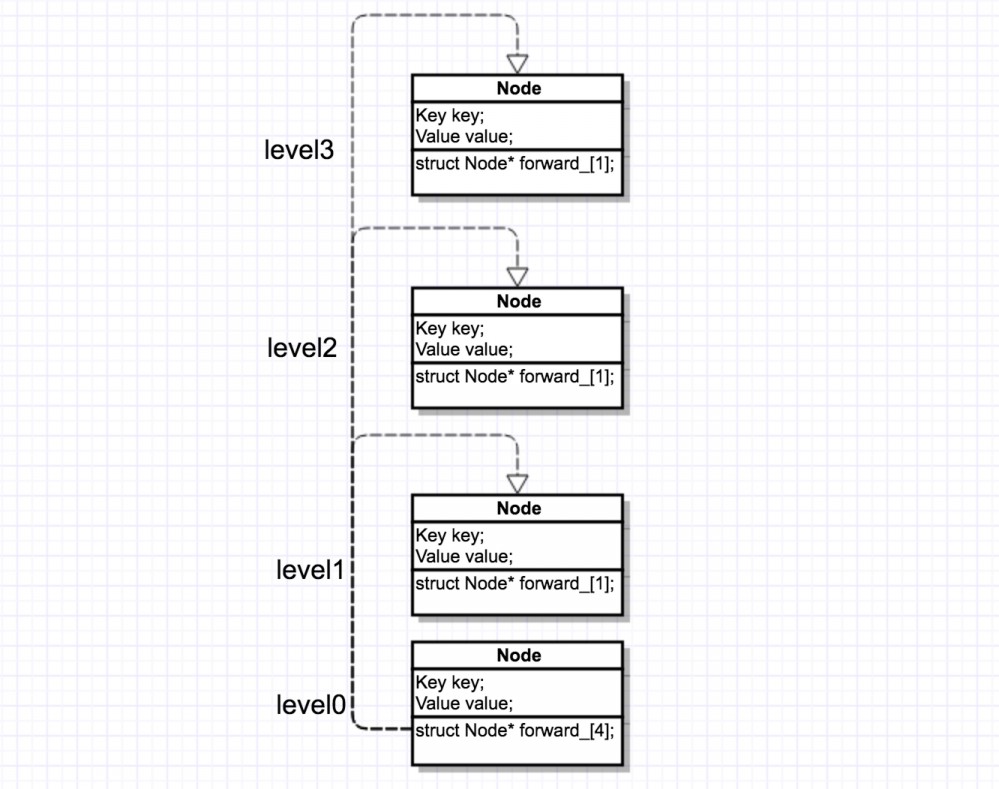
跳表的深入浅出——SkipList

代码生成了图6.1的结构，level0 节点的 forward_ 数组大小为4，leve1 ~ level3 都为空节点，但是分配了 8 个字节的指针内存 (64位操作系统)。图中虚线为数组引用表达，并不是指针指向。

随机层数生成数方法实现

取自google开源项目leveldb的实现

template <typename Key, typename Value>
int SkipList<Key, Value>::randomLevel() {

  static const unsigned int kBranching = 4;
  int height = 1;
  while (height < kMaxLevel && ((::Next(rnd_) % kBranching) == 0)) {
    height++;
  }
  assert(height > 0);
  assert(height <= kMaxLevel);
  return height;
}

uint32_t Next( uint32_t& seed) {
  seed = seed & 0x7fffffffu; // 防止负数

  if (seed == 0 || seed == 2147483647L) { 
    seed = 1;
  }

  static const uint32_t M = 2147483647L;   // 2^31-1
  static const uint64_t A = 16807;  // bits 14, 8, 7, 5, 2, 1, 0
  // We are computing
  //       seed_ = (seed_ * A) % M,    where M = 2^31-1
  //
  // seed_ must not be zero or M, or else all subsequent computed values
  // will be zero or M respectively.  For all other values, seed_ will end
  // up cycling through every number in [1,M-1]
  uint64_t product = seed * A;

  // Compute (product % M) using the fact that ((x << 31) % M) == x.
  seed = static_cast<uint32_t>((product >> 31) + (product & M));
  // The first reduction may overflow by 1 bit, so we may need to
  // repeat.  mod == M is not possible; using > allows the faster
  // sign-bit-based test.
  if (seed > M) {
    seed -= M;
  }
  return seed;
}

总体来说这个 level 层数的生成方法也不是随机的，根据 seed 不断被修改的次数来决定层数，换而言之就是 level0 节点数量来决定层数。

有关节点结构体的方法实现

template <typename Key, typename Value>
void 
SkipList<Key, Value>::SetNext(int i, Node* x) {
	assert(i >= 0);
    forward_[i] = x; // 设置数组节点
}

template <typename Key, typename Value>
void 
SkipList<Key, Value>::Node* Next(int i) {
	assert(i >= 0);
    return forward_[i];
}

SetNext(int i, Node* x) 方法是设置 forward_ 节点数组第 i 层(level)的链表引用。

例如图6.1 中，key=10 调用了 SetNext(4, Node where key = 20 and level = 4) 和 key=20 调用了 SetNext(4, Node where key = 40 and level = 4) 的表述。

图 6.2

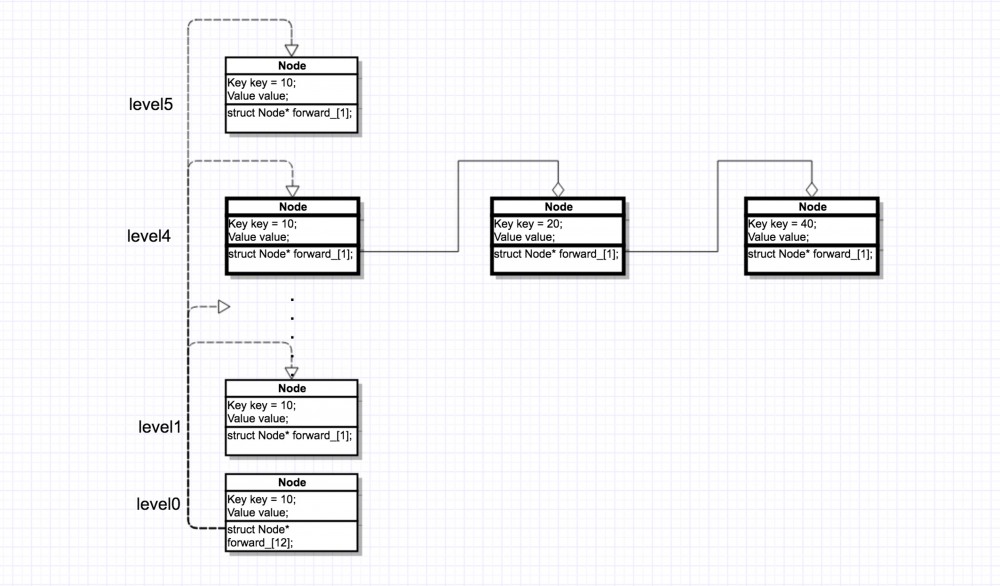
Next(int i) 为取出某层节点链表的方法，这个应该不应解析了吧。

输出跳表结构

template <typename Key, typename Value>
void
SkipList<Key, Value>::Print()
{
  Node* next, *x = head_;

  printf("--------/n");
  for (int i = level_ - 1; i >= 0; --i) {
    x = head_;
    while ((next = x->Next(i))) {
      x = next;
      std::cout << "key: " << next->key << " -> ";
    }
    printf("/n");
  }
  printf("--------/n");
}

Print 方法来输出查看当前跳表有哪些节点结构

参考资料：

跳表SkipList

Skip List（跳跃表）原理详解与实现

原文 https://simplecodesky.com/2018/04/16/skiplist-deep-learning/

正文到此结束