转载

NAACL 2018 杰出论文：RNN作为识别器，判定加权语言一致性

4月11日，NAACL 2018公布了四篇杰出论文，分别关注于词表征、语句映射、文本生成和RNN。机器之心对最后一篇论文进行了编译介绍，该论文探索了识别加权语言的RNN形式模型的计算复杂度。研究表明，大多数类似的RNN中存在的问题都是不可判定的，包括：一致性、等价性、最小化和最高权重字符串的确定。然而，对于连续一致的RNN来说，最后一个问题是可判定的。

NAACL2018杰出论文。

循环神经网络（RNNs）是一种令人瞩目的概率语言建模方法（Mikolov and Zweig, 2012）。近来，许多实验都表明 RNN 在通过分配概率生成英语文本任务上显著优于其他方法（Jozefowicz et al., 2016）。

简单来说，RNN 的工作方式大致如下。在每一个时间步，它接收一个输入词项，更新它的隐状态向量，然后通过生成一个基于词汇表的概率分布来预测下一个时间步的词项。输入字符串的概率由构成字符串的词项（后面跟随一个终止符）的预测概率乘积得到。在这种模式下，每一个 RNN 都定义了一种加权语言，即一个从字符串到权重的全函数。

Siegelmann 和 Sontag 1995 年的一项工作表明使用了饱和线性激活函数的有合适权重的单层 RNN 可以计算任何可计算的函数。一个带有 886 个隐单元的特定架构可以实时地模拟任何图灵机（用 RNN 的每一个时间步来模拟图灵机的每一步）。然而，其中使用的 RNN 会把全部输入编码为它的内部状态，在接收到终止符时进行实际的计算，然后在一个特定的隐单元中编码输出。在这种方式下，RNN 在编码输入后可以有一定时间进行」思考」，这和图灵机的计算时间是等价的。

我们考虑一种不同的 RNN 的变体，它被广泛应用于自然语言处理的应用中。它使用 ReLU 作为激活函数，在每一个时刻接收输入词项，然后对下一个词项的概率分布进行预测。接下来，在读入上一个输入词项之后，它会立刻停下来，同时我们简单地把每一个时刻的输入词项预测的积作为权重分配给输入。

我们现在对于其他被用于概率语言建模的形式化方法，比如有限状态自动机和上下文无关语法等已经有了充分的理解。它们的可用性很大程度上直接来源于较为完善的算法属性。举例来说，加权有限状态自动机计算出的加权语言在交（逐点乘积）和并（逐点和）下关闭，相应的未加权语言在交、并、差和补下关闭 (Droste et al., 2013)。此外，类似于 OpenFST (Allauzen et al., 2007) 和 Carmel1 的工具箱实现了许多基于自动机的高效算法，比如：最小化、交、找到最高权重路径和最高权重字符串。

RNN 从业者自然面对许多这些相同的问题。例如，基于 RNN 的机器翻译系统应该提取由 RNN 生成的最高权重的输出字符串（即最可能的翻译）(Sutskever et al., 2014; Bahdanau et al., 2014)。目前，这项任务可以通过启发式贪婪和束搜索等近似技术来解决。最小化技术对于在存储空间有限的设备（如移动电话）上部署大型 RNN 是非常有益的。目前我们仅有像知识蒸馏 (Kim and Rush, 2016) 等启发式方法。同时，我们是否能确定计算出的加权语言的一致性也尚不清楚（即它是否一组所有字符串的概率分布）。如果没有确定分配给所有有限字符串的整体概率集群，就难以对语言模型的困惑度进行公平比较。

本文的目标是研究 RNN 的 ReLU 变体的上述问题。更具体地说，研究者提出并回答以下问题：

一致性：RNN 计算出的加权语言是否一致？计算出的加权语言的一致性是否可判定？
最高权重字符串：我们能否（有效）确定计算的加权语言中权重最高的字符串？
等价性：我们是否可以决定两个给定的 RNN 是否计算相同的加权语言？
最小化：我们是否可以最小化给定 RNN 的神经元数量？

论文：Recurrent Neural Networks as Weighted Language Recognizers（使用循环神经网络作为加权语言识别器）

NAACL 2018 杰出论文：RNN作为识别器，判定加权语言一致性

论文地址：https://arxiv.org/pdf/1711.05408.pdf

我们探索了不同问题下用于识别加权语言的循环神经网络形式模型的计算复杂度。我们主要关注被广泛使用于自然语言处理任务中的单层的、使用 ReLU 作为激活函数的、被合理分配权重且带有 softmax 层的循环神经网络。我们的工作表明，大多数类似的循环神经网络中存在的问题都是不可判定的，包括：一致性、等价性、最小化和最高权重字符串的确定。然而，对于连续一致的循环神经网络来说，尽管解决方案的长度会超过所有计算能力的上限，最后一个问题是可判定的。如果我们把字符串限定在多项式的长度，那么这个问题就可以变成 NP 完全和 APX-hard 问题。总的来说，这说明在这些循环神经网络的实际应用中，近似和启发式的算法是很有必要的。

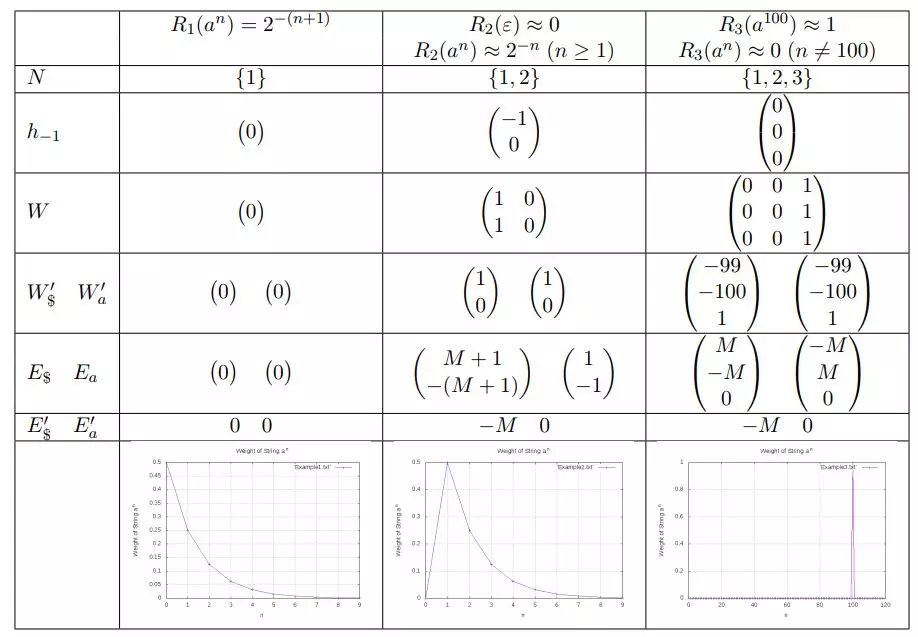
NAACL 2018 杰出论文：RNN作为识别器，判定加权语言一致性