Java集合——TreeMap(一)
TreeMap底层是红黑树,在java8 HashMap也引入了红黑树,那么什么是红黑树?红黑树是一种二叉搜索树,它在每个结点上增加了一个存储位来表示结点的颜色,可以是RED或BLACK。通过对任何一条从根到叶子的简单路径上各个结点的颜色进行约束,红黑树确保没有一条路径会比其他路径长出2倍,因而是近似于平衡的。(出自算法导论)
二叉搜搜索树
既然红黑树是一种二叉搜索树,那么我们先来了解其性质:
①.左子树上所有结点的值小于或等于其根结点的值
②.右子树上所有结点的值大于或等于其根结点的值
③.任意节点的左、右子树也分别为二叉搜索树
如下:
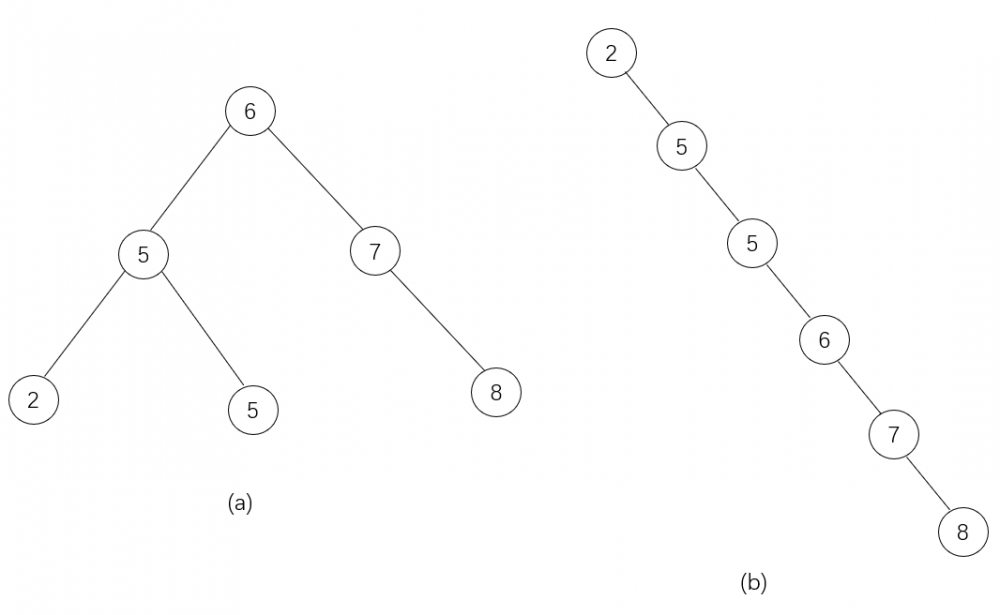
虽然图a,图b都是二叉搜索树,但是若同时找值为8的结点。这两种结构明显图a查找所费时间更少。为了保证树的结构左右两端数据大致平衡降低二叉树的查询难度一般会采用一种算法机制实现节点数据结构的平衡,实现了这种算法的有比如AVL、红黑树,使用平衡二叉树能保证数据的左右两边的结点层级相差不会大于1,通过这样避免树形结构由于增加删除变成线性链表影响查询效率,保证数据平衡的情况下查找数据的速度近于二分法查找。
红黑树
红黑树是每个节点都带有颜色属性的二叉搜索树,颜色或红色或黑色。除了符合二叉搜索的基本特性外,它还附加如下性质:
①.节点是红色或黑色
②.根节点是黑色
③.每个叶节点(NIL节点,空节点)是黑色的
④.每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
⑤.从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点
一颗典型的红黑树:
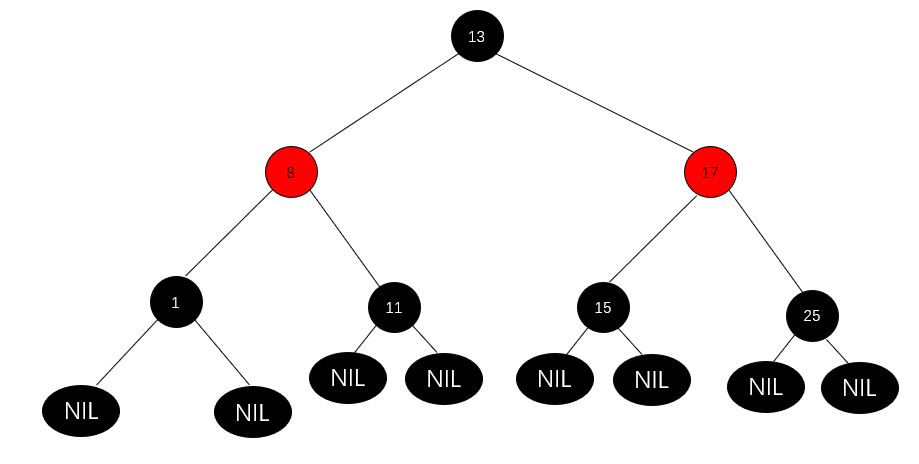
当我们对红黑树进行插入和删除等操作时,可能会破坏红黑树的性质。为了保证红黑树始终是一颗红黑树,其通过旋转、变色进行调整.而旋转又分成两种形式:
左旋:
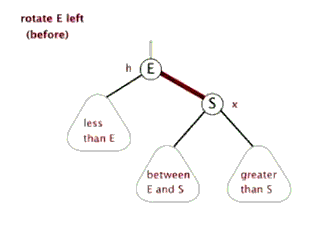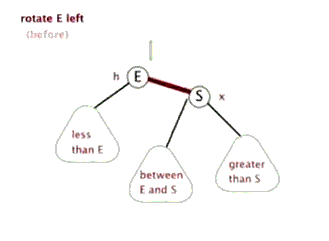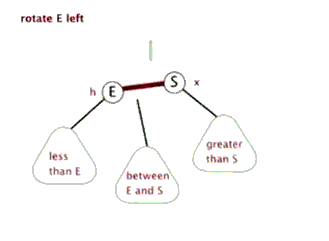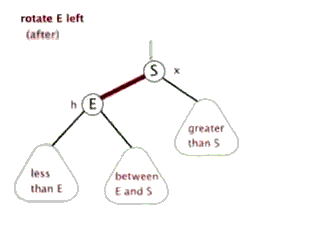
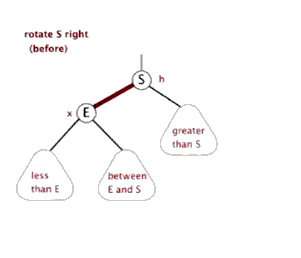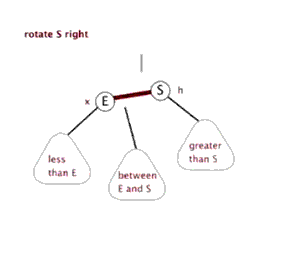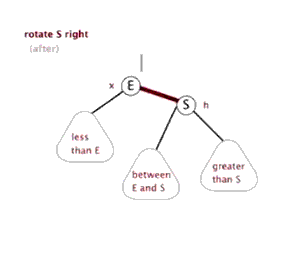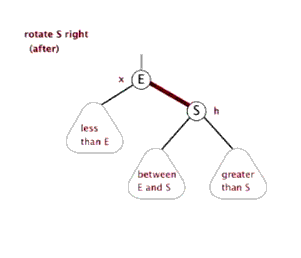
右旋:
TreeMap
言归正传回到treeMap,我们先看下它的继承关系图:
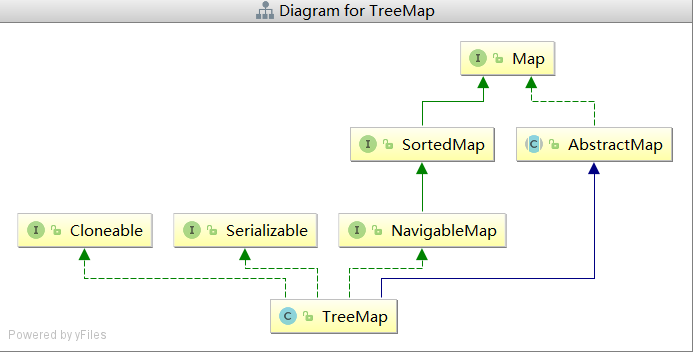
TreeMap重要字段
// 比较器用于排序,若为null使用自然排序维持key顺序
private final Comparator comparator;
// 根节点
private transient Entry root;
// 节点数
private transient int size = 0;
// 修改次数,fail-fast
private transient int modCount = 0;
//节点颜色
private static final boolean RED = false;
private static final boolean BLACK = true;
/**
* 节点
*/
static final class Entry implements Map.Entry {
K key; //键
V value; //值
Entry left; //左子树
Entry right; //右子树
Entry parent; //父亲
boolean color = BLACK; //颜色
Entry(K key, V value, Entry parent) {...}
public K getKey() {...}
public V getValue() {...}
public V setValue(V value) {...}
public boolean equals(Object o) {...}
public int hashCode() {...}
public String toString() {...}
}
构造方法
/**
* 无参构造,自然排序(从小到大)。要求key实现Comparable接口,会调用key重写的compareTo方法进行比较
* 若key没有实现comparable接口,运行时报错(java.lang.ClassCastException)
*/
public TreeMap() {
comparator = null;
}
/**
* 指定比较器,若不为null会调用其compare方法进行比较,无需键实现comparable接口
*/
public TreeMap(Comparator comparator) {
this.comparator = comparator;
}
/**
* 将map转为treeMap,比较器为null,注意key
*/
public TreeMap(Map m) {
comparator = null;
putAll(m);
}
/**
* 将map转为treeMap,比较器为SortMap中的comparator
*/
public TreeMap(SortedMap m) {
comparator = m.comparator();
try {
buildFromSorted(m.size(), m.entrySet().iterator(), null, null);
} catch (java.io.IOException cannotHappen) {
} catch (ClassNotFoundException cannotHappen) {
}
}
put方法
public V put(K key, V value) {
// 获取根节点
Entry t = root;
// 若TreeMap为空则直接插入
if (t == null) {
//校验:若比较器为null则key必须实现Comparable接口,若不为null,key可为null
compare(key, key); // type (and possibly null) check
//设为头节点
root = new Entry<>(key, value, null);
size = 1;
modCount++;
return null;
}
// 记录key排序比较结果
int cmp;
// 记录父节点
Entry parent;
// split comparator and comparable paths
Comparator cpr = comparator;
// 若存在比较器,循环查找位置cmp小于0往左找,大于0往右找,直至等于0进行替换
if (cpr != null) {
do {
parent = t;
cmp = cpr.compare(key, t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
// 若不存在比较器,key必须实现Comparable接口
else {
//null无法实现Comparable接口没有compareTo方法故抛异常
if (key == null)
throw new NullPointerException();
//获取比较器,处理方式与上面一致
@SuppressWarnings("unchecked")
Comparable k = (Comparable) key;
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
//若当前TreeMap中没有此key则新建结点,无论上述哪个分支成立parent一定指向当前某个叶子结点
Entry e = new Entry<>(key, value, parent);
//小于0则为左子树
if (cmp < 0)
parent.left = e;
//大于0则为右子树
else
parent.right = e;
//保证红黑树性质
fixAfterInsertion(e);
size++;
modCount++;
return null;
}
get方法
get方法与put思路大致相同
public V get(Object key) {
Entry p = getEntry(key);
//找到对应节点返回其值,没有找到返回null
return (p==null ? null : p.value);
}
final Entry getEntry(Object key) {
// Offload comparator-based version for sake of performance
// 若比较器不为null
if (comparator != null)
return getEntryUsingComparator(key);
// 若比较器为null,则key必须实现Comparable接口,null不能抛异常
if (key == null)
throw new NullPointerException();
//用key的compareTo方法,从根节点寻找,若没有找返回null
@SuppressWarnings("unchecked")
Comparable k = (Comparable) key;
Entry p = root;
while (p != null) {
int cmp = k.compareTo(p.key);
if (cmp < 0)
p = p.left;
else if (cmp > 0)
p = p.right;
else
return p;
}
return null;
}
final Entry getEntryUsingComparator(Object key) {
@SuppressWarnings("unchecked")
K k = (K) key;
Comparator cpr = comparator;
//处理方式一致
if (cpr != null) {
Entry p = root;
while (p != null) {
int cmp = cpr.compare(k, p.key);
if (cmp < 0)
p = p.left;
else if (cmp > 0)
p = p.right;
else
return p;
}
}
return null;
}
containsValue方法
采用类似中序遍历(LDR左根右)方式来遍历整个红黑树找到相应value
public boolean containsValue(Object value) {
for (Entry e = getFirstEntry(); e != null; e = successor(e))
if (valEquals(value, e.value))
return true;
return false;
}
/**
* 返回最小节点
*/
final Entry getFirstEntry() {
Entry p = root;
if (p != null)
while (p.left != null)
p = p.left;
return p;
}
/**
* 找后继节点
*/
static TreeMap.Entry successor(Entry t) {
if (t == null)
return null;
//若存在右子树,则返回右子树中最小节点
else if (t.right != null) {
Entry p = t.right;
while (p.left != null)
p = p.left;
return p;
//若不存在,从当前节点往上找,若其父节点不为null且它是父节点的右子树则继续找父节点
//直至条件不成立,返回父节点
} else {
Entry p = t.parent;
Entry ch = t;
while (p != null && ch == p.right) {
ch = p;
p = p.parent;
}
return p;
}
}
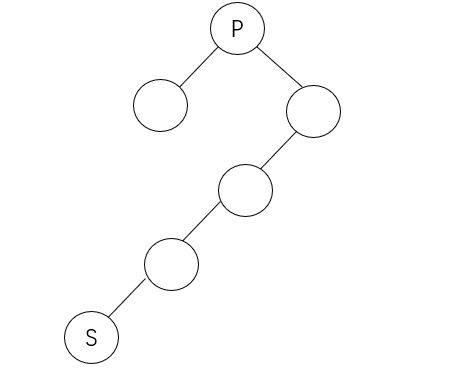
successor方法找节点的后继节点:
①.若节点为空没有后继
②.若节点有右子树,后继为右子树的最左节点
③.若节点没有右子树,后继为该节点所在左子树的第一个祖先节点
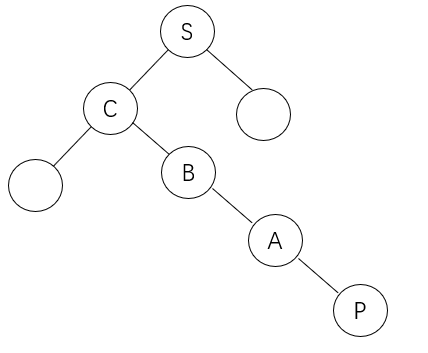
第一个无需多言,第二个也容易,看图p的后继节点s:
第三个:
若其父节点为空,返回null;
若其有父节点且为父节点左子树,返回其父节点;
若其有父节点且为父节点右子树,其所在左子树的第一个祖先节点看图(p的后继为s),一个个往上找将p与A看成整体相对于B是其右子树,再往上找将P、B、A看成整体相对于C还是其右子树,再找P、B、A、C整体相对于S是其左子树,返回这个整体的第一个祖先节点即节点S
remove方法
public V remove(Object key) {
//获取key所对应的节点
Entry p = getEntry(key);
//若节点为空返回null
if (p == null)
return null;
//若不为null,删除节点返回其值
V oldValue = p.value;
deleteEntry(p);
return oldValue;
}
private void deleteEntry(Entry p) {
modCount++;
size--;
//若p左子树和右子树都不为null,将p的key与value替换成后继的,将p指向后继
if (p.left != null && p.right != null) {
Entry s = successor(p);
p.key = s.key;
p.value = s.value;
p = s;
} // p has 2 children
// replacement为替代节点
Entry replacement = (p.left != null ? p.left : p.right);
if (replacement != null) {
replacement.parent = p.parent;
//若p没有父节点,则根节点设为replacement
if (p.parent == null)
root = replacement;
//若p为左节点,则用replacement替换左节点
else if (p == p.parent.left)
p.parent.left = replacement;
//若p为右节点,则用replacement替换右节点
else
p.parent.right = replacement;
//删除p节点
p.left = p.right = p.parent = null;
// 若p为黑色则需要调整
if (p.color == BLACK)
fixAfterDeletion(replacement);
//若p没有父节点即p为根节点,根节点置空
} else if (p.parent == null) { // return if we are the only node.
root = null;
//p没有子节点
} else { // No children. Use self as phantom replacement and unlink.
if (p.color == BLACK)
fixAfterDeletion(p);
//删除p节点
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
}
分三种情况:
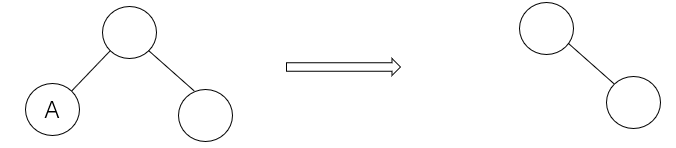
①.叶子结点:直接将其父节点对应孩子置空,若删除左叶子结点则将其父结点左子树置空,若删除右叶子结点则将其父结点右子树置空
删除节点A:
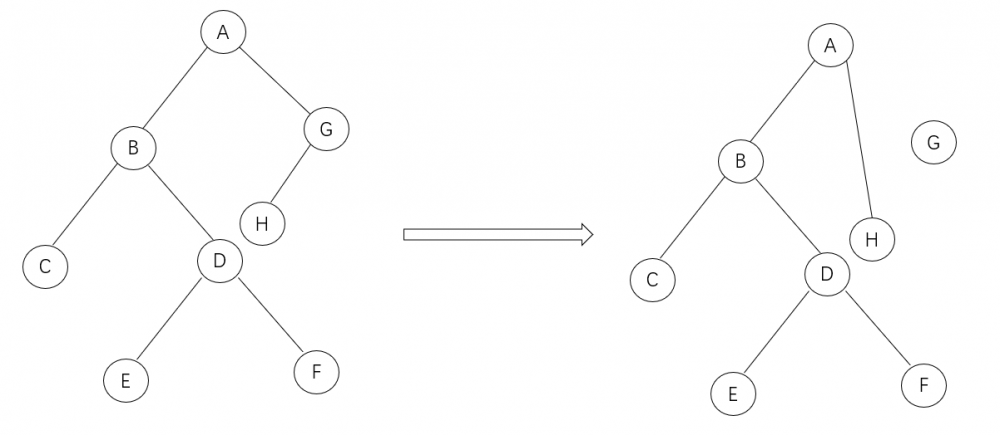
②.一个孩子:用子节点替代需删除节点
删除节点G:
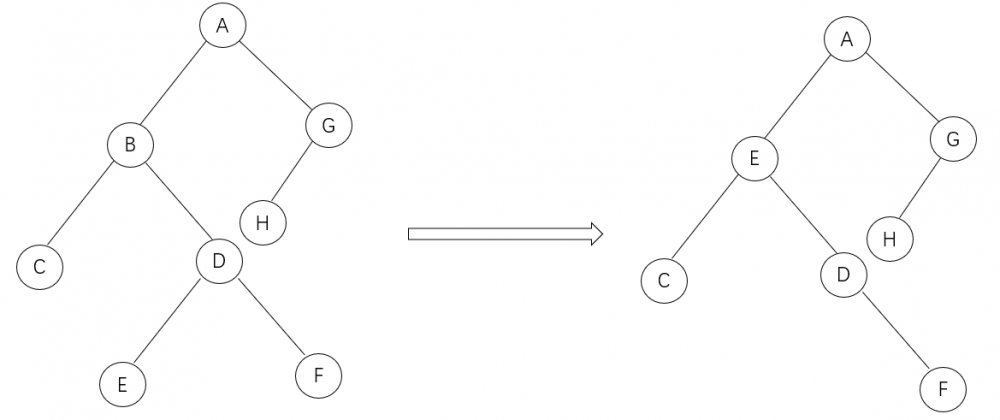
③.两个孩子:先找到后继,找到后,替换当前节点的内容为后继节点,然后再删除后继节点,因为这个后继节点一定没有左孩子,所以就将两个孩子的情况转换为了前面两种情况
删除节点B:










![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)

