二叉查找树 - 删除节点 详解(Java实现)
在浏览 二叉查找树(三)之 Java的实现 时,发现所有操作都很容易理解,只有 删除 看的很糊涂。原文作者在方法上也没有任何注释,因此理解起来很不容易。因此本文是在这篇的基础上,对 删除 操作进行详细的讲解,所以如果你对二叉查找树还不了解,先看前面这篇博客,如果你能直接看懂那篇博客中的删除方法,也不必再看本文。
虽然我自己也完全从头实现了一遍二叉查找树,但是为了和前面这篇博客衔接的更好,这里就直接拿这篇博客的代码来说明,并且会对删除操作进行简单的调整。
完整的代码在本文最后,在测试类中还提供了一个简单的输出树结构的工具类。
删除节点
删除节点存在 3 种情况,几乎所有类似博客都提到了这点。这 3 种情况分别如下:
- 没有左右子节点,可以直接删除
- 存在左节点或者右节点,删除后需要对子节点移动
- 同时存在左右子节点,不能简单的删除,但是可以通过和 后继 节点交换后转换为前两种情况
实际上在 3 种情况中,还有一个特例就是删除 根节点 ,后续代码会有处理。
下面,我们使用图详细来说说怎么删除。
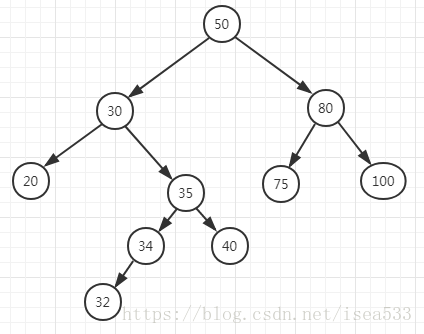
初始状态如下图所示,我们可以按照 50, 30, 80, 20, 35, 34, 32, 40, 70, 75, 100 的顺序插入到树中,就会产生下图所示的树。
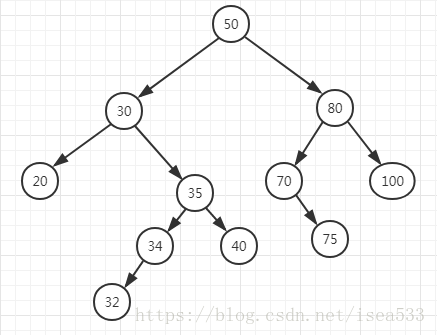
下面按照这 3 种情况分别来讲。
1. 没有左右子节点时
在我们图中,符合这个条件的有 20,32,40,75,100,随便找个 20 来演示删除该节点:
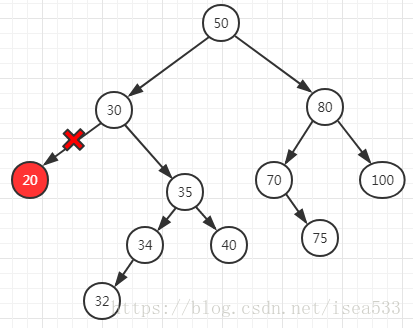
这种情况是最简单的,我们只需要删除该节点和父节点的关系即可。删除的时候需要先判断自己和父节点的关系是左侧还是右侧,判断方式很简单,如下:
//这里忽略了父节点不存在的情况,最后会巧妙的处理这种情况
if(node.parent.left == node){
node.parent.left = null;
} else {
node.parent.right = null;
}
如果父节点的左节点是自己,就清左侧,否则就是右侧。删除后如下图所示:
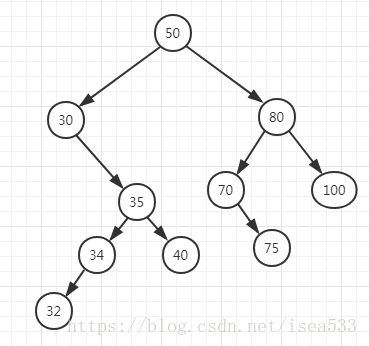
2. 存在左节点或者右节点时
满足这个情况的节点有 34, 70 两个节点,这里以 70 为例,如下图所示:
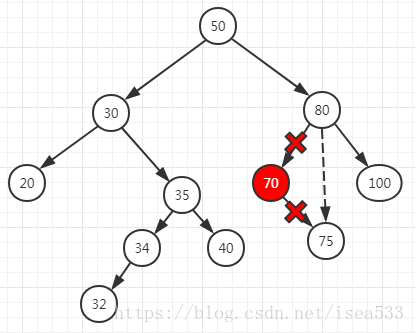
删除 70 的时候,需要断两个关系,然后建立父节点和子节点的关系,代码如下:
//先找到子节点,不需要管他是左是右
BSTNode<T> child = null;
if(node.left != null){
child = node.left;
} else {
child = node.right;
}
//这里忽略了父节点不存在的情况,最后会巧妙的处理这种情况
//将父节点和子节点建立关系
if(node.parent.left == node){
node.parent.left = child;
} else {
node.parent.right = child;
}
child.parent = node.parent;
经过上述操作后,节点状态如下图所示:
3. 同时存在左右子节点
满足 同时存在左右节点 的节点有 50,30,80,35 这 4 个节点,30 看起来更复杂,我们以 30 为例。
当二叉查找树以中序遍历时,遍历的结果是一个从小到大排列的顺序,如下图所示:
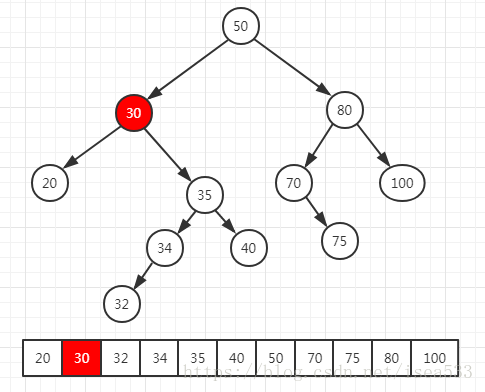
当我们删除 30 节点的时候,整个中序遍历的结果中,从 32 开始都往前移动了一位。32 是 30 的 后继节点 ,就是比 30 大的节点中最小的节点。当某个节点存在右节点时,后继结点就是右节点中的最小值,由于左侧节点总比右侧节点和父节点小,所以 后继 节点一定没有左节点。从这一个特点就能看出来,后继结点有可能存在右节点,也有可能没有任何节点。后继结点还有一个特点,就是他比 30 的左节点大,比 30 所有的右节点都小,因此删除 30 的时候,可以直接将后继结点 32 的值( key )转移到 30 节点上,然后删除后继结点 32。由于后继结点最多只有一个子节点,因此删除 后继 节点时,就变成了 3 种情况中的前两种。图示如下:
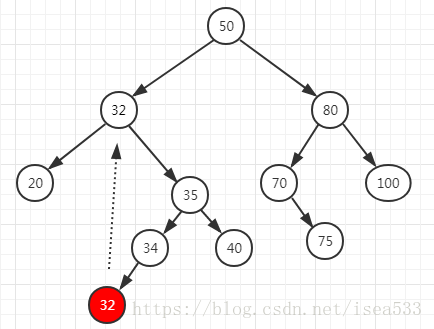
转移节点值的代码很容易:
//获取当前节点的后继结点 Node<T> successor = successor(node); //转移值 node.key = successor.key; //后续变成删除 successor,就变成了前两种情况 //在图示例子中,就是第一种没有子节点的情况 node = successor;
看到这里应该都不难,没什么问题,接下来开始将 3 种情况合并到一起处理,先按照本文的逻辑来写。
整合 3 种情况的删除
代码如下,详细说明看注释
private BSTNode<T> delete(BSTNode<T> node) {
//第 3 种情况,如果同时存在左右子节点
if (node.left != null && node.right != null){
//获取后继结点
BSTNode<T> successor = successor(node);
//转移后继结点值到当前节点
node.key = successor.key;
//把要删除的当前节点设置为后继结点
node = successor;
}
//经过前一步处理,下面只有前两种情况,只能是一个节点或者没有节点
//不管是否有子节点,都获取子节点
BSTNode<T> child;
if (node.left != null)
child = node.left;
else
child = node.right;
//如果 child != null,就说明是有一个节点的情况
if (child != null)
//将子节点和父节点关联上
child.parent = node.parent;
//如果当前节点没有父节点(后继情况到这儿时一定有父节点)
//说明要删除的就是根节点
if (node.parent == null)
//根节点设置为子节点
//按照前面逻辑,根只有一个或者没有节点,所以直接赋值 child 即可
mRoot = child;
else if (node == node.parent.left)//存在父节点,并且当前节点是左节点时
//将父节点的左节点设置为 child
node.parent.left = child;
else//右节点时
//将父节点的右节点设置为 child
node.parent.right = child;
//返回被删除的节点
return node;
}
//删除指定的值
public void delete(T key) {
//获取要删除的节点
BSTNode<T> node = search(mRoot, key);
//如果存在就删除
if (node != null)
delete(node);
}
在上面这段代码中,和原文相比不一样,这里对后继结点的处理更好理解。
通过前面的铺垫和这里的代码注释,删除这个操作应该能真正领会了,下面针对 二叉查找树(三)之 Java的实现 中的删除,增加注释,代码如下:
/*
* 删除结点(z),并返回被删除的结点
*
* 参数说明:
* bst 二叉树
* z 删除的结点
*/
private BSTNode<T> remove(BSTree<T> bst, BSTNode<T> z) {
//这里没起个好名字,让人看着默默奇妙,实际上 x 就是子节点 child
BSTNode<T> x=null;
//这里的 y 节点就是要删除的节点 delete
BSTNode<T> y=null;
//这个写法理解比较绕,不如反转后容易理解
//只有一个节点或者没有节点时
if ((z.left == null) || (z.right == null) )
//z 就是要删除的节点
y = z;
else
//当有两个子节点时,删除后继结点
y = successor(z);
//获取子节点,不管是左是右
if (y.left != null)
x = y.left;
else
x = y.right;
//如果存在子节点,就关联被删节点的父节点
if (x != null)
x.parent = y.parent;
//如果父节点是空,说明要删的是根节点
if (y.parent == null)
//设置根为 child(此时根只有一个或没有节点)
bst.mRoot = x;
else if (y == y.parent.left)//要删的是左节点
y.parent.left = x;//左节点关联子节点
else//要删的是右节点
y.parent.right = x;//右节点关联子节点
//如果要删的节点和一开始传入的不一样,就是后继的情况
if (y != z)
z.key = y.key;//后继的值传给本来要删除的节点
//返回被删除的节点
return y;
}
/*
* 删除结点(z),并返回被删除的结点
*
* 参数说明:
* tree 二叉树的根结点
* z 删除的结点
*/
public void remove(T key) {
BSTNode<T> z, node;
if ((z = search(mRoot, key)) != null)
if ( (node = remove(this, z)) != null)
node = null;
}
理解前面代码后,再看上面这段代码也不难理解。所有代码中都没有处理 node 节点的上下级关系,因为通过其他节点已经无法引用到该 node 节点了,所以 node 能被 GC 正常回收。
完整代码
下面包含了完整的二叉查找树代码,90% 来自于前面的那篇博客,增加了删除节点注释和上面增加的 delete 方法,后面还有一个测试和输出树节点的代码,最后有测试输出的结果。
树代码
/**
* Java 语言: 二叉查找树
*
* @author skywang
* @date 2013/11/07
*/
public class BSTree<T extends Comparable<T>> {
BSTNode<T> mRoot; // 根结点
public class BSTNode<T extends Comparable<T>> {
T key; // 关键字(键值)
BSTNode<T> left; // 左孩子
BSTNode<T> right; // 右孩子
BSTNode<T> parent; // 父结点
public BSTNode(T key, BSTNode<T> parent, BSTNode<T> left, BSTNode<T> right) {
this.key = key;
this.parent = parent;
this.left = left;
this.right = right;
}
public T getKey() {
return key;
}
public String toString() {
return "key:"+key;
}
}
public BSTree() {
mRoot=null;
}
/*
* 前序遍历"二叉树"
*/
private void preOrder(BSTNode<T> tree) {
if(tree != null) {
System.out.print(tree.key+" ");
preOrder(tree.left);
preOrder(tree.right);
}
}
public void preOrder() {
preOrder(mRoot);
}
/*
* 中序遍历"二叉树"
*/
private void inOrder(BSTNode<T> tree) {
if(tree != null) {
inOrder(tree.left);
System.out.print(tree.key+" ");
inOrder(tree.right);
}
}
public void inOrder() {
inOrder(mRoot);
}
/*
* 后序遍历"二叉树"
*/
private void postOrder(BSTNode<T> tree) {
if(tree != null)
{
postOrder(tree.left);
postOrder(tree.right);
System.out.print(tree.key+" ");
}
}
public void postOrder() {
postOrder(mRoot);
}
/*
* (递归实现)查找"二叉树x"中键值为key的节点
*/
private BSTNode<T> search(BSTNode<T> x, T key) {
if (x==null)
return x;
int cmp = key.compareTo(x.key);
if (cmp < 0)
return search(x.left, key);
else if (cmp > 0)
return search(x.right, key);
else
return x;
}
public BSTNode<T> search(T key) {
return search(mRoot, key);
}
/*
* (非递归实现)查找"二叉树x"中键值为key的节点
*/
private BSTNode<T> iterativeSearch(BSTNode<T> x, T key) {
while (x!=null) {
int cmp = key.compareTo(x.key);
if (cmp < 0)
x = x.left;
else if (cmp > 0)
x = x.right;
else
return x;
}
return x;
}
public BSTNode<T> iterativeSearch(T key) {
return iterativeSearch(mRoot, key);
}
/*
* 查找最小结点:返回tree为根结点的二叉树的最小结点。
*/
private BSTNode<T> minimum(BSTNode<T> tree) {
if (tree == null)
return null;
while(tree.left != null)
tree = tree.left;
return tree;
}
public T minimum() {
BSTNode<T> p = minimum(mRoot);
if (p != null)
return p.key;
return null;
}
/*
* 查找最大结点:返回tree为根结点的二叉树的最大结点。
*/
private BSTNode<T> maximum(BSTNode<T> tree) {
if (tree == null)
return null;
while(tree.right != null)
tree = tree.right;
return tree;
}
public T maximum() {
BSTNode<T> p = maximum(mRoot);
if (p != null)
return p.key;
return null;
}
/*
* 找结点(x)的后继结点。即,查找"二叉树中数据值大于该结点"的"最小结点"。
*/
public BSTNode<T> successor(BSTNode<T> x) {
// 如果x存在右孩子,则"x的后继结点"为 "以其右孩子为根的子树的最小结点"。
if (x.right != null)
return minimum(x.right);
// 如果x没有右孩子。则x有以下两种可能:
// (01) x是"一个左孩子",则"x的后继结点"为 "它的父结点"。
// (02) x是"一个右孩子",则查找"x的最低的父结点,并且该父结点要具有左孩子",找到的这个"最低的父结点"就是"x的后继结点"。
BSTNode<T> y = x.parent;
while ((y!=null) && (x==y.right)) {
x = y;
y = y.parent;
}
return y;
}
/*
* 找结点(x)的前驱结点。即,查找"二叉树中数据值小于该结点"的"最大结点"。
*/
public BSTNode<T> predecessor(BSTNode<T> x) {
// 如果x存在左孩子,则"x的前驱结点"为 "以其左孩子为根的子树的最大结点"。
if (x.left != null)
return maximum(x.left);
// 如果x没有左孩子。则x有以下两种可能:
// (01) x是"一个右孩子",则"x的前驱结点"为 "它的父结点"。
// (01) x是"一个左孩子",则查找"x的最低的父结点,并且该父结点要具有右孩子",找到的这个"最低的父结点"就是"x的前驱结点"。
BSTNode<T> y = x.parent;
while ((y!=null) && (x==y.left)) {
x = y;
y = y.parent;
}
return y;
}
/*
* 将结点插入到二叉树中
*
* 参数说明:
* tree 二叉树的
* z 插入的结点
*/
private void insert(BSTree<T> bst, BSTNode<T> z) {
int cmp;
BSTNode<T> y = null;
BSTNode<T> x = bst.mRoot;
// 查找z的插入位置
while (x != null) {
y = x;
cmp = z.key.compareTo(x.key);
if (cmp < 0)
x = x.left;
else
x = x.right;
}
z.parent = y;
if (y==null)
bst.mRoot = z;
else {
cmp = z.key.compareTo(y.key);
if (cmp < 0)
y.left = z;
else
y.right = z;
}
}
/*
* 新建结点(key),并将其插入到二叉树中
*
* 参数说明:
* tree 二叉树的根结点
* key 插入结点的键值
*/
public void insert(T key) {
BSTNode<T> z=new BSTNode<T>(key,null,null,null);
// 如果新建结点失败,则返回。
if (z != null)
insert(this, z);
}
private BSTNode<T> delete(BSTNode<T> node) {
//第 3 种情况,如果同时存在左右子节点
if (node.left != null && node.right != null){
//获取后继结点
BSTNode<T> successor = successor(node);
//转移后继结点值到当前节点
node.key = successor.key;
//把要删除的当前节点设置为后继结点
node = successor;
}
//经过前一步处理,下面只有前两种情况,只能是一个节点或者没有节点
//不管是否有子节点,都获取子节点
BSTNode<T> child;
if (node.left != null)
child = node.left;
else
child = node.right;
//如果 child != null,就说明是有一个节点的情况
if (child != null)
//将子节点和父节点关联上
child.parent = node.parent;
//如果当前节点没有父节点(后继情况到这儿时一定有父节点)
//说明要删除的就是根节点
if (node.parent == null)
//根节点设置为子节点
//按照前面逻辑,根只有一个或者没有节点,所以直接赋值 child 即可
mRoot = child;
else if (node == node.parent.left)//存在父节点,并且当前节点是左节点时
//将父节点的左节点设置为 child
node.parent.left = child;
else//右节点时
//将父节点的右节点设置为 child
node.parent.right = child;
//返回被删除的节点
return node;
}
//删除指定的值
public void delete(T key) {
//获取要删除的节点
BSTNode<T> node = search(mRoot, key);
//如果存在就删除
if (node != null)
delete(node);
}
/*
* 删除结点(z),并返回被删除的结点
*
* 参数说明:
* bst 二叉树
* z 删除的结点
*/
private BSTNode<T> remove(BSTree<T> bst, BSTNode<T> z) {
//这里没起个好名字,让人看着默默奇妙,实际上 x 就是子节点 child
BSTNode<T> x=null;
//这里的 y 节点就是要删除的节点 delete
BSTNode<T> y=null;
//这个写法理解比较绕,不如反转后容易理解
//只有一个节点或者没有节点时
if ((z.left == null) || (z.right == null) )
//z 就是要删除的节点
y = z;
else
//当有两个子节点时,删除后继结点
y = successor(z);
//获取子节点,不管是左是右
if (y.left != null)
x = y.left;
else
x = y.right;
//如果存在子节点,就关联被删节点的父节点
if (x != null)
x.parent = y.parent;
//如果父节点是空,说明要删的是根节点
if (y.parent == null)
//设置根为 child(此时根只有一个或没有节点)
bst.mRoot = x;
else if (y == y.parent.left)//要删的是左节点
y.parent.left = x;//左节点关联子节点
else//要删的是右节点
y.parent.right = x;//右节点关联子节点
//如果要删的节点和一开始传入的不一样,就是后继的情况
if (y != z)
z.key = y.key;//后继的值传给本来要删除的节点
//返回被删除的节点
return y;
}
/*
* 删除结点(z),并返回被删除的结点
*
* 参数说明:
* tree 二叉树的根结点
* z 删除的结点
*/
public void remove(T key) {
BSTNode<T> z, node;
if ((z = search(mRoot, key)) != null)
if ( (node = remove(this, z)) != null)
node = null;
}
/*
* 销毁二叉树
*/
private void destroy(BSTNode<T> tree) {
if (tree==null)
return ;
if (tree.left != null)
destroy(tree.left);
if (tree.right != null)
destroy(tree.right);
tree=null;
}
public void clear() {
destroy(mRoot);
mRoot = null;
}
/*
* 打印"二叉查找树"
*
* key -- 节点的键值
* direction -- 0,表示该节点是根节点;
* -1,表示该节点是它的父结点的左孩子;
* 1,表示该节点是它的父结点的右孩子。
*/
private void print(BSTNode<T> tree, T key, int direction) {
if(tree != null) {
if(direction==0) // tree是根节点
System.out.printf("%2d is root/n", tree.key);
else // tree是分支节点
System.out.printf("%2d is %2d's %6s child/n", tree.key, key, direction==1?"right" : "left");
print(tree.left, tree.key, -1);
print(tree.right,tree.key, 1);
}
}
public void print() {
if (mRoot != null)
print(mRoot, mRoot.key, 0);
}
}
测试代码
public class BSTreeTest {
public static BSTree<Integer> newTree() {
int[] array = new int[]{50, 30, 80, 20, 35, 34, 32, 40, 70, 75, 100};
BSTree<Integer> tree = new BSTree<>();
for (int i = 0; i < array.length; i++) {
tree.insert(array[i]);
}
return tree;
}
public static void main(String[] args) {
BSTree<Integer> tree = newTree();
System.out.println("----------初始--------");
print(tree);
tree.delete(20);
System.out.println("----------删除 20--------");
print(tree);
tree = newTree();
tree.delete(70);
System.out.println("----------删除 70--------");
print(tree);
tree = newTree();
tree.delete(30);
System.out.println("----------删除 30--------");
print(tree);
}
//------------下面代码是用于输出树的工具代码------------------------
public static final String PREFIX_BRANCH = "├";//树枝
public static final String PREFIX_TRUNK = "│ ";//树干
public static final String PREFIX_LEAF = "└";//叶子
public static final String PREFIX_EMP = " ";//空
public static final String PREFIX_LEFT = "─L─";//左
public static final String PREFIX_RIGTH = "─R─";//右
private static boolean hasChild(BSTree.BSTNode node){
return node.left != null || node.right != null;
}
public static void print(BSTree tree){
if(tree != null && tree.mRoot != null){
System.out.println(tree.mRoot.key);
print(tree.mRoot, "");
}
}
public static void print(BSTree.BSTNode node, String prefix){
if(prefix == null){
prefix = "";
} else {
prefix = prefix.replace(PREFIX_BRANCH, PREFIX_TRUNK);
prefix = prefix.replace(PREFIX_LEAF, PREFIX_EMP);
}
if(hasChild(node)){
if(node.right != null){
System.out.println(prefix + PREFIX_BRANCH + PREFIX_RIGTH + node.right.key);
if(hasChild(node.right)){
print(node.right, prefix + PREFIX_BRANCH);
}
} else {
System.out.println(prefix + PREFIX_BRANCH + PREFIX_RIGTH);
}
if(node.left != null){
System.out.println(prefix + PREFIX_LEAF + PREFIX_LEFT + node.left.key);
if(hasChild(node.left)){
print(node.left, prefix + PREFIX_LEAF);
}
} else {
System.out.println(prefix + PREFIX_LEAF + PREFIX_LEFT);
}
}
}
}
测试结果
注意:每次删除都在在初始树的状态下删除的,不是在同一个树连续执行的。
----------初始-------- 50 ├─R─80 │ ├─R─100 │ └─L─70 │ ├─R─75 │ └─L─ └─L─30 ├─R─35 │ ├─R─40 │ └─L─34 │ ├─R─ │ └─L─32 └─L─20 ----------删除 20-------- 50 ├─R─80 │ ├─R─100 │ └─L─70 │ ├─R─75 │ └─L─ └─L─30 ├─R─35 │ ├─R─40 │ └─L─34 │ ├─R─ │ └─L─32 └─L─ ----------删除 70-------- 50 ├─R─80 │ ├─R─100 │ └─L─75 └─L─30 ├─R─35 │ ├─R─40 │ └─L─34 │ ├─R─ │ └─L─32 └─L─20 ----------删除 30-------- 50 ├─R─80 │ ├─R─100 │ └─L─70 │ ├─R─75 │ └─L─ └─L─32 ├─R─35 │ ├─R─40 │ └─L─34 └─L─20











![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)

