每日一博 | 梯度下降法求多元线性回归及 Java 实现
正文

梯度下降法求多元线性回归及Java实现
顶
原
荐
冷
冷血狂魔
发布于 前天 19:28字数 1613
阅读 109
收藏 8
点赞 1
评论 0
Java
华为云4核8G,高性能云服务器,免费试用 >>> 
对于数据分析而言,我们总是极力找数学模型来描述数据发生的规律, 有的数据我们在二维空间就可以描述,有的数据则需要映射到更高维的空间。数据表现出来的分布可能是完全离散的,也可能是聚集成堆的,那么机器学习的任务就是让计算机自己在数据中学习到数据的规律。那么这个规律通常是可以用一些函数来描述,函数可能是线性的,也可能是非线性的,怎么找到这些函数,是机器学习的首要问题。
本篇博客尝试用梯度下降法,找到线性函数的参数,来拟合一个数据集。
假设我们有如下函数  ,其中x是一个三个维度,
,其中x是一个三个维度,
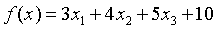
写一个java程序来,随机产生100笔数据作为训练集。
Random random = new Random();
double[] results = new double[100];
double[][] features = new double[100][3];
for (int i = 0; i < 100; i++) {
for (int j = 0; j < features[i].length; j++) {
features[i][j] = random.nextDouble();
}
results[i] = 3 * features[i][0] + 4 * features[i][1] + 5 * features[i][2] + 10;
}
上面的程序中results就是函数的值,features的第二维就是随机产生的3个x。
有了训练集,我们的任务就变成了如何求出3个各种的系数3、4、5,以及偏移量10,系数和偏移量可以取任意值,那么我们就得到了一个函数集,任务转化一下就变成了找出一个函数作用于训练集之后,与真实值的误差最小,如何评判误差的大小呢?我们需要定义一个函数来评判,那么给这个函数取一个名字,叫损失函数。这里,损失函数定义为  ,其中
,其中  为真实值,问题就转化为在训练集中求如下函数:
为真实值,问题就转化为在训练集中求如下函数:
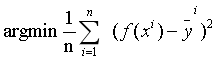
如何求这个函数的极小值呢?如果我们计算能力无限大,直接穷举就完了,但是这不是高效的办法,这时候就说的了梯度下降法,我们来看看数学里对梯度的定义。
在微积分里面,对多元函数的参数求∂偏导数,把求得的各个参数的偏导数以向量的形式写出来,就是梯度。比如函数f(x,y), 分别对x,y求偏导数,求得的梯度向量就是(∂f/∂x, ∂f/∂y)T,简称grad f(x,y)或者▽f(x,y)。
梯度告诉我们两件事情:
1、函数增大的方向
2、我们走向增大的方向,应该走多大步幅
求极小值,我们反方向走即可,加个负号,但是这个步幅有个问题,如果过大,参数就直接飞出去了,就很难在找到最小值,如果太小,则很有可能卡在局部极小值的地方。所以,我们设计了一个系数来调节步幅,我们叫它学习速率learningRate。
好了,为了好描述,我们把上面的函数泛化一下,表示成如下公式:
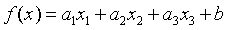
损失函数对每个参数求偏导数,根据偏导数值,当然求导的过程需要用到链式法则,,这里我们直接给出参数更新公式如下:
对于BGD(批量梯度下降法):
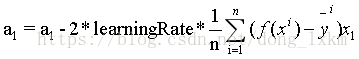
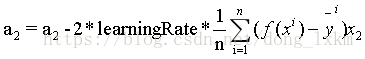
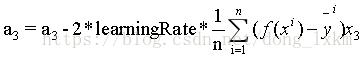
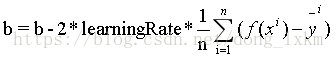
对于SGD(随机梯度下降法),SGD与BGD不同的是每笔数据,我们都更新一次参数,效率比较低下。公式和上面类似,去掉求和符号和除以N即可。
下面是具体的代码实现
import java.util.Random;
public class LinearRegression {
public static void main(String[] args) {
// y=3*x1+4*x2+5*x3+10
Random random = new Random();
double[] results = new double[100];
double[][] features = new double[100][3];
for (int i = 0; i < 100; i++) {
for (int j = 0; j < features[i].length; j++) {
features[i][j] = random.nextDouble();
}
results[i] = 3 * features[i][0] + 4 * features[i][1] + 5 * features[i][2] + 10;
}
double[] parameters = new double[] { 1.0, 1.0, 1.0, 1.0 };
double learningRate = 0.01;
for (int i = 0; i < 30; i++) {
SGD(features, results, learningRate, parameters);
}
parameters = new double[] { 1.0, 1.0, 1.0, 1.0 };
System.out.println("==========================");
for (int i = 0; i < 3000; i++) {
BGD(features, results, learningRate, parameters);
}
}
private static void SGD(double[][] features, double[] results, double learningRate, double[] parameters) {
for (int j = 0; j < results.length; j++) {
double gradient = (parameters[0] * features[j][0] + parameters[1] * features[j][1]
+ parameters[2] * features[j][2] + parameters[3] - results[j]) * features[j][0];
parameters[0] = parameters[0] - 2 * learningRate * gradient;
gradient = (parameters[0] * features[j][0] + parameters[1] * features[j][1] + parameters[2] * features[j][2]
+ parameters[3] - results[j]) * features[j][1];
parameters[1] = parameters[1] - 2 * learningRate * gradient;
gradient = (parameters[0] * features[j][0] + parameters[1] * features[j][1] + parameters[2] * features[j][2]
+ parameters[3] - results[j]) * features[j][2];
parameters[2] = parameters[2] - 2 * learningRate * gradient;
gradient = (parameters[0] * features[j][0] + parameters[1] * features[j][1] + parameters[2] * features[j][2]
+ parameters[3] - results[j]);
parameters[3] = parameters[3] - 2 * learningRate * gradient;
}
double totalLoss = 0;
for (int j = 0; j < results.length; j++) {
totalLoss = totalLoss + Math.pow((parameters[0] * features[j][0] + parameters[1] * features[j][1]
+ parameters[2] * features[j][2] + parameters[3] - results[j]), 2);
}
System.out.println(parameters[0] + " " + parameters[1] + " " + parameters[2] + " " + parameters[3]);
System.out.println("totalLoss:" + totalLoss);
}
private static void BGD(double[][] features, double[] results, double learningRate, double[] parameters) {
double sum = 0;
for (int j = 0; j < results.length; j++) {
sum = sum + (parameters[0] * features[j][0] + parameters[1] * features[j][1]
+ parameters[2] * features[j][2] + parameters[3] - results[j]) * features[j][0];
}
double updateValue = 2 * learningRate * sum / results.length;
parameters[0] = parameters[0] - updateValue;
sum = 0;
for (int j = 0; j < results.length; j++) {
sum = sum + (parameters[0] * features[j][0] + parameters[1] * features[j][1]
+ parameters[2] * features[j][2] + parameters[3] - results[j]) * features[j][1];
}
updateValue = 2 * learningRate * sum / results.length;
parameters[1] = parameters[1] - updateValue;
sum = 0;
for (int j = 0; j < results.length; j++) {
sum = sum + (parameters[0] * features[j][0] + parameters[1] * features[j][1]
+ parameters[2] * features[j][2] + parameters[3] - results[j]) * features[j][2];
}
updateValue = 2 * learningRate * sum / results.length;
parameters[2] = parameters[2] - updateValue;
sum = 0;
for (int j = 0; j < results.length; j++) {
sum = sum + (parameters[0] * features[j][0] + parameters[1] * features[j][1]
+ parameters[2] * features[j][2] + parameters[3] - results[j]);
}
updateValue = 2 * learningRate * sum / results.length;
parameters[3] = parameters[3] - updateValue;
double totalLoss = 0;
for (int j = 0; j < results.length; j++) {
totalLoss = totalLoss + Math.pow((parameters[0] * features[j][0] + parameters[1] * features[j][1]
+ parameters[2] * features[j][2] + parameters[3] - results[j]), 2);
}
System.out.println(parameters[0] + " " + parameters[1] + " " + parameters[2] + " " + parameters[3]);
System.out.println("totalLoss:" + totalLoss);
}
}
运行结果如下:
同样是更新3000次参数。
1、SGD结果:
参数分别为:3.087332784857909 、4.075233812033048 、5.06020828348889、 9.89116046652793
totalLoss:0.13515381461776949
2、BGD结果:
参数分别为:3.0819123489025344 、4.064145151461403、5.046862571520019、 9.899847277313173
totalLoss:0.1050937019067582
可以看出,BGD有更好的表现。
快乐源于分享。
此博客乃作者原创, 转载请注明出处
© 著作权归作者所有
共有人打赏支持
冷
冷血狂魔
粉丝 71
博文 33
码字总数 38510
作品 0
杭州
程序员
相关文章 最新文章
上一篇博客《梯度下降法求多元线性回归及Java实现》简单了介绍了梯度下降法,并用Java实现了一个梯度下降法求回归的例子。本篇博客,尝试用dl4j的张量运算库nd4j来实现梯度下降法求多元线性回...
冷血狂魔
前天
0
0
一、牛顿法概述 除了前面说的梯度下降法,牛顿法也是机器学习中用的比较多的一种优化算法。牛顿法的基本思想是利用迭代点处的一阶导数(梯度)和二阶导数(Hessen矩阵)对目标函数进行二次函数近...
google19890102
2014/11/13
0
0
上一篇我们提到了单变量的线性回归模型,但是我们实际遇到的问题,都会有多个变量影响,比如上篇的例子——房价问题,在实际情况下影响房价的一定不止房子的面积,房子的地理位置,采光度等等...
机智的神棍酱
06/18
0
0
前言: 最近打算稍微系统的学习下deep learing的一些理论知识,打算采用Andrew Ng的网页教程UFLDLTutorial,据说这个教程写得浅显易懂,也不太长。不过在这这之前还是复习下machine lea...
东方神剑
2015/10/26
0
0
目录: 多变量线性回归(模型、梯度下降技巧) 特征选择和多项式回归 正规方程 Matlab学习 1 多变量线性回归1)模型 - 假设函数: - 参数:全部的 theta - 代价函数:和单变量回归一样 - 梯度...
kevinbetterq
03/05
0
0
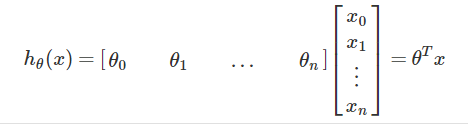
正规方程(LinearRegression) 梯度下降(SGDRegressor) 适用于小规模数据集 适用于大规模数据集 一次运算得出 需要指定学习率, 须多次运算(迭代)得出 只适用于线性模型(可能出现过拟合问题) 适...
木子昭
01/14
0
0

1. 梯度下降法简介 以下是定义了一个损失函数以后,参数theta对应的损失函数J的值对应的示例图,我们需要找到使得损失函数值J取得最小值对应的theta(这里是二维平面,也就是我们的参数只有一...
Meet相识_bfa5
04/22
0
0
求解线性回归最常用的两个方法是:梯度下降法和最小二乘法,之前在文章《机器学习:用梯度下降法实现线性回归》中介绍了梯度下降法的工作流程等,这篇文章着重介绍最小二乘法的使用。由于最小...
cyan_soul
03/25
0
0
Question 29. Divide Two Integers Solution 题目大意:给定两个数字,求出它们的商,要求不能使用乘法、除法以及求余操作。 思路:说下用移位实现的方法 Java实现: 法1:如果可以用除法,一...
yysue
07/06
0
0
阅读原文请访问我的博客 BrightLoong's Blog 一. 简介 提醒篇幅较大需耐心。 简介来自ThreadLocal类注释 ThreadLocal类提供了线程局部 (thread-local) 变量。这些变量与普通变量不同,每个线...
BrightLoong
05/28
0
0

没有更多内容
加载失败,请刷新页面
加载更多下一页
1任何事都没有表面看起来那么简单 2所有的事都会比你预计的时间长 3可能出错的事总会出错 4如果你担心某种情况发生,那么它就更有可能发生 系统划分时,也要考虑康威定律 1系统架构是公司组织...
writeademo
2分钟前
0
0
一、概述 redis3.2发布rc版本已经有一段时间了,估计RedisConf 2016左右,3.2版本就能release了。3.2版本中增加的最大功能就是对GEO(地理位置)的支持。说起redis的GEO特性,最大的贡献还是...
IT--小哥
7分钟前
0
0
https://www.oschina.net/p/pbgo
chai2010
44分钟前
0
0
linux下的文件同步工具 rsync rsync是非常实用的一个同步工具,可以从a机器到b机器传输一个文件,也可以备份数据,系统默认没有这个工具,要使用命令 yum install -y rsync 安装。 rsync的命...
黄昏残影
今天
0
0
Osc乱弹歌单(2018)请戳(这里) 【今日歌曲】 @哈哈哈哈哈嗝:一定要听——The Pancakes的单曲《咁咁咁》 《咁咁咁》- The Pancakes 手机党少年们想听歌,请使劲儿戳(这里) @clouddyy :...
小小编辑
今天
382
4

重磅:让人类得老年痴呆的竟是它? Lala 2018-07-19 1.今日导读 去年奥斯卡最佳动画长片《寻梦环游记》里有一句经典台词:“比死亡更可怕的,是遗忘”。在电影中,年迈的曾祖母会重复说一样的...
aibinxiao
今天
3
0
Linux机器之间以密码方式互相登录 运行命令#ssh [ip address],标准命令:#ssh [username]@ip, 如果没有写用户名,则默认为系统当前登录的用户 命令#w查看系统负载,可查看到连接到该主机的...
小丑鱼00
今天
0
0
昨天元芳做了git分支管理规范的分享,为了拓展大家关于git分支的认知,这里我特意再分享这两个关于git flow的链接,大家可以看一下。 Git 工作流程 Git分支管理策略 git flow本质上是...
qwfys
今天
2
0
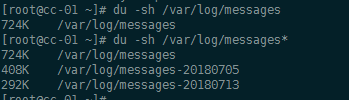
/var/log/messages linux系统总日志 /etc/logrotate.conf 日志切割配置文件 参考https://my.oschina.net/u/2000675/blog/908189 dmesg命令 dmesg’命令显示linux内核的环形缓冲区信息,我们可...
chencheng-linux
今天
1
0
下载镜像 前往 树莓派官网 下载镜像。 点击 最新版Raspbian 下载最新版镜像。 下载后请,通过 访达 双击解压,或通过 unzip 命令解压。 检查下载的文件 ls -lh -rw-r--r-- 1 dingdayu s...
dingdayu
今天
3
0
没有更多内容
加载失败,请刷新页面
加载更多下一页
- 本文标签: 线程 Deep Learning Google REST 云 源码 下载 UI 本质 空间 update 主机 Features 管理 组织 linux 服务器 文章 系统架构 模型 注释 src ssh https message IDE value 备份 python 配置 id 时间 同步 java git 免费 redis DOM rsync 博客 安装 IO 代码 参数 目录 ip 2015 数据 Git Flow 程序员 zip http
- 版权声明: 本文为互联网转载文章,出处已在文章中说明(部分除外)。如果侵权,请联系本站长删除,谢谢。
- 本文海报: 生成海报一 生成海报二











![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)

