转载

【Leetcode】62. 不同路径

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

例如，上图是一个7 x 3 的网格。有多少可能的路径？

说明：m 和 n 的值均不超过 100。

示例 1:

输入: m = 3, n = 2
输出: 3
解释:
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右
复制代码

示例 2:

输入: m = 7, n = 3
输出: 28
复制代码

题解

这道题拿到题目我觉得大家的第一反应都是这应该是递归的题目,因为我们可以转化为子问题，但是这样暴力肯定会超时,就不用尝试了。其实在该题递归的方法就是从上面到下面不断的去尝试,如果我们能记住之前的结果,就对我们下一步有帮助,所以想到了DP的方法。格子中的数字代表当前的方法.

初始状态
当前这个状态只和左边和上边的格子有关系.
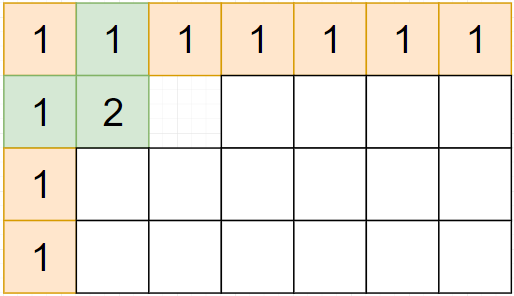
依次求解

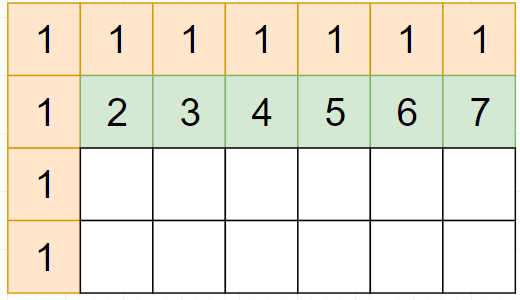
于是我们可以得到状态转移方程：

ways[i][j] = ways[i-1][j] + ways[i][j-1];
复制代码

java代码

public class Solution {
    public int uniquePaths(int m, int n) {
        int[][] ways = new int[m][n];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (i == 0 || j == 0) ways[i][j] = 1;
                else ways[i][j] = ways[i-1][j] + ways[i][j-1];
            }
        }
        return ways[m-1][n-1];
    }
}
复制代码

优化

上面图3我们在求解的时候,我们是一行一行求解的,实际上我们只需要记录遍历到(i, j)这个位置的时候当前行有几种路径,如果遍历到(i, m-1)的时候,替换掉这一行对应列的路径即可，于是状态转移方程编程: res[j] = res[j] + res[j-1]

class Solution {
    public int uniquePaths(int m, int n) {
        if (m <= 0 || n <= 0) {
            return 0;
        }
        int[] res = new int[n];
        res[0] = 1;
        for (int i = 0; i < m; i++) {
            for (int j = 1; j < n; j++) {
                res[j] += res[j - 1];
                System.out.println("i=" + i + "_" + "j=" + j + ":" + Arrays.toString(res));
            }
        }
        return res[n - 1];
    }
}
复制代码

有的同学可能还是不理解,我在代码里面打印了一些信息方便理解：

i=0_j=1:[1, 1, 0, 0, 0, 0, 0]
i=0_j=2:[1, 1, 1, 0, 0, 0, 0]
i=0_j=3:[1, 1, 1, 1, 0, 0, 0]
i=0_j=4:[1, 1, 1, 1, 1, 0, 0]
i=0_j=5:[1, 1, 1, 1, 1, 1, 0]
i=0_j=6:[1, 1, 1, 1, 1, 1, 1] //只记录到这一行的信息
i=1_j=1:[1, 2, 1, 1, 1, 1, 1]
i=1_j=2:[1, 2, 3, 1, 1, 1, 1]
i=1_j=3:[1, 2, 3, 4, 1, 1, 1]
i=1_j=4:[1, 2, 3, 4, 5, 1, 1]
i=1_j=5:[1, 2, 3, 4, 5, 6, 1]
i=1_j=6:[1, 2, 3, 4, 5, 6, 7] //只记录到这一行的信息
i=2_j=1:[1, 3, 3, 4, 5, 6, 7]
i=2_j=2:[1, 3, 6, 4, 5, 6, 7]
i=2_j=3:[1, 3, 6, 10, 5, 6, 7]
i=2_j=4:[1, 3, 6, 10, 15, 6, 7]
i=2_j=5:[1, 3, 6, 10, 15, 21, 7]
i=2_j=6:[1, 3, 6, 10, 15, 21, 28] //只记录到这一行的信息
i=3_j=1:[1, 4, 6, 10, 15, 21, 28]
i=3_j=2:[1, 4, 10, 10, 15, 21, 28]
i=3_j=3:[1, 4, 10, 20, 15, 21, 28]
i=3_j=4:[1, 4, 10, 20, 35, 21, 28]
i=3_j=5:[1, 4, 10, 20, 35, 56, 28]
i=3_j=6:[1, 4, 10, 20, 35, 56, 84] //只记录到这一行的信息
复制代码

Math

这个题其实可以用排列组合的方式来做。这其实是最开始想到的方法。以模拟的[4, 7]的例子,每一条路径：

向右的肯定有6步;
向左的肯定有3步; 问题即为:c(9,3) = (9 * 8 * 7) / (1 * 2 * 3) = 84

组合数公式：c(m,n) = m! / (n! * (m - n)!)

java代码

java直接套用公式会越界,下面结果我用long存储:

1!=1
2!=2
3!=6
4!=24
5!=120
6!=720
7!=5040
8!=40320
9!=362880
10!=3628800
11!=39916800
12!=479001600
13!=6227020800
14!=87178291200
15!=1307674368000
16!=20922789888000
17!=355687428096000
18!=6402373705728000
19!=121645100408832000
20!=2432902008176640000
21!=-4249290049419214848
22!=-1250660718674968576
23!=8128291617894825984
24!=-7835185981329244160
复制代码

需要稍微化简一下,化简的过程就是我求解c(9,3)的第二步骤。

class Solution {
    public int uniquePaths(int m, int n) {
        double dom = 1;
        double dedom = 1;
        int small = m < n ? m - 1 : n - 1;
        int big = m < n ? n - 1 : m - 1;
        for (int i = 1; i <= small; i++) {
            dedom *= i;
            dom *= small + big + 1 - i;
        }
        return (int) (dom / dedom);
    }
}
复制代码

python代码

python代码就比较凶残了,一行代码搞定:

class Solution:
    def uniquePaths(self, m, n):
        return int(math.factorial(m + n - 2) / math.factorial(m -1) / math.factorial(n-1))
复制代码

贴一下DP版本的代码

class Solution:
    def uniquePaths(self, m, n):
        """
        :type m: int
        :type n: int
        :rtype: int
        """
        if m <= 0 or n <= 0:
            return 0
        res = [0 for _ in range(0, n)]
        res[0] = 1
        for i in range(0, m):
            for j in range(1, n):
                res[j] += res[j-1]
        return res[n-1]
复制代码

原文 https://juejin.im/post/5b927e795188255c6c621e11

正文到此结束