java版JieBa分词源码走读 -- Trie树、Viterbi算法与HMM
List<SegToken> process = segmenter.process("今天早上,出门的的时候,天气很好", JiebaSegmenter.SegMode.INDEX);
for (SegToken token:process){
//分词的结果
System.out.println( token.word);
}
复制代码
输出内容如下
今天 早上 , 出门 的 的 时候 , 天气 很 好 复制代码
分词的执行逻辑
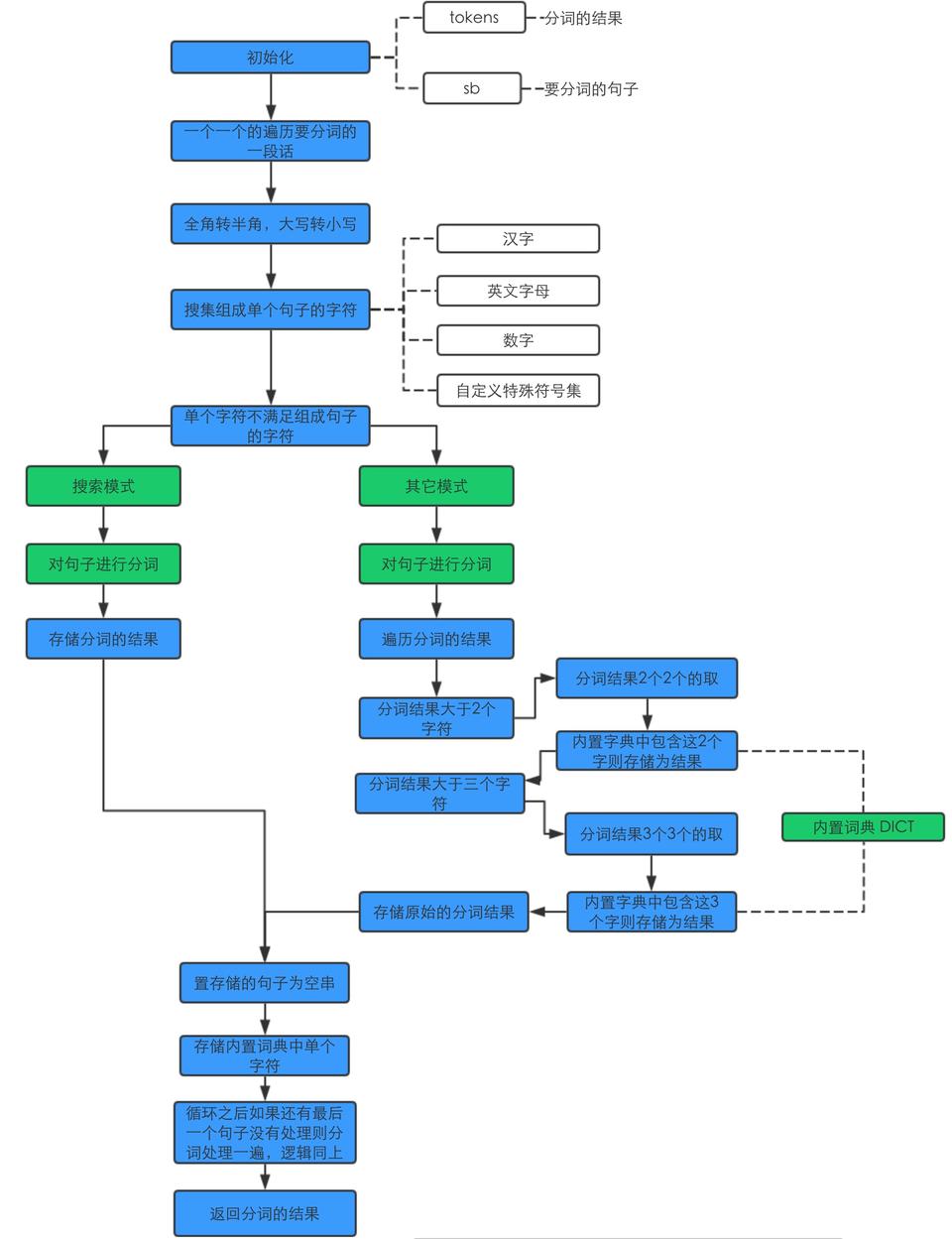
可以看到核心在于
- 内部包含一个字典
- 分词逻辑
- 不同模式的切分粒度
分词的模式
- search 精准的切开,用于对用户查询词分词
- index 对长词再切分,提高召回率
分词流程
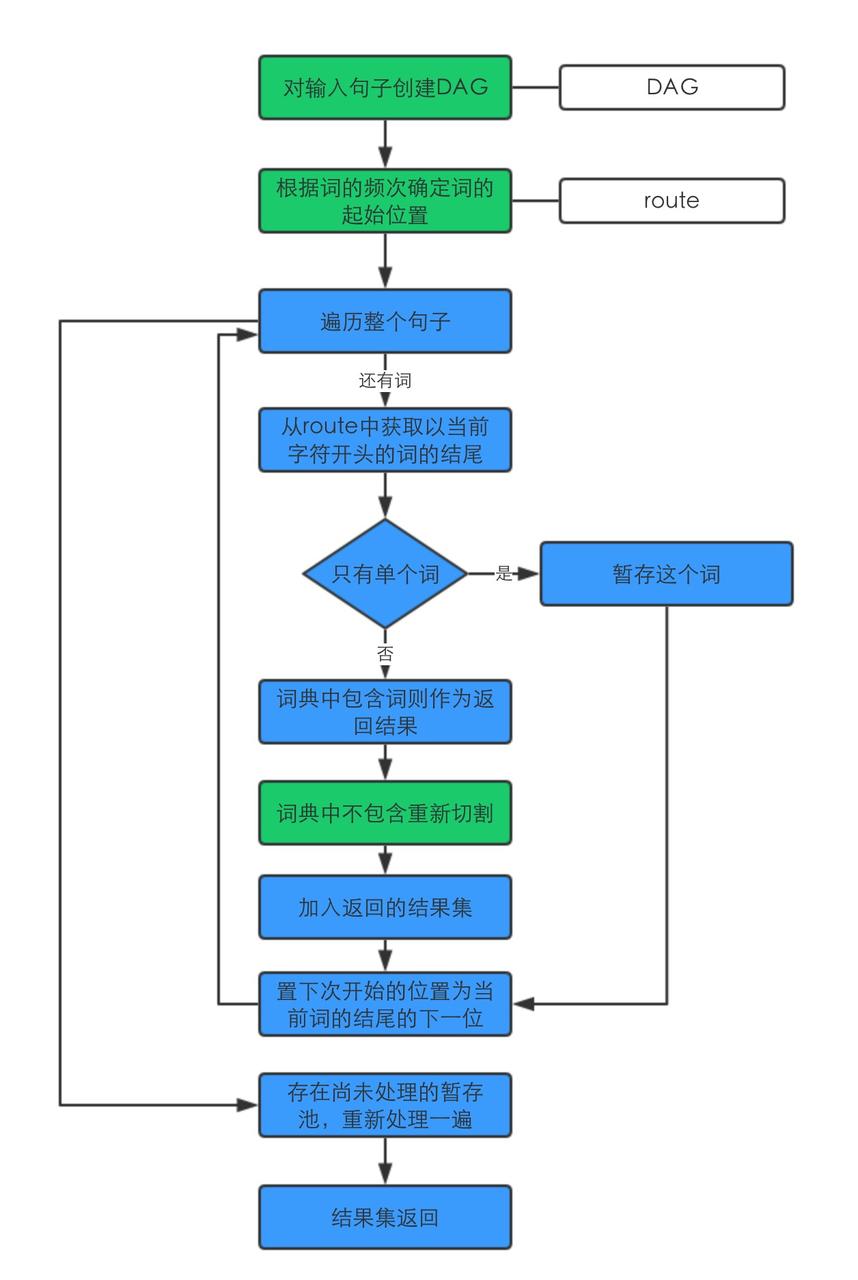
可以看到核心在于
- 根据输入创建DAG
- 选取高频的词
- 词典中不包含的情况下,即未记录词,进行重新识别
创建DAG
- 获取已经加载的trie树
- 从trie树中匹配,核心代码如下
int N = chars.length; //获取整个句子的长度 int i = 0, j = 0; //i 表示词的开始 ;j 表示词的结束 while (i < N) { Hit hit = trie.match(chars, i, j - i + 1); //从trie树中匹配 if (hit.isPrefix() || hit.isMatch()) { if (hit.isMatch()) { //完全匹配 if (!dag.containsKey(i)) { List<Integer> value = new ArrayList<Integer>(); dag.put(i, value); value.add(j); } else dag.get(i).add(j); //以当前字符开头的词有哪些,词结尾的坐标记下来 } j += 1; if (j >= N) { //以当前字符开头的所有词已经匹配完成,再以当前字符的下一个字符开头寻找词 i += 1; j = i; } } else { //以当前字符开头的词已经全部匹配完成,再以当前字符的下一个字符开头寻找词 i += 1; j = i; } } 复制代码 - 补充DAG中没有出现的句子中的字符
DAG结果示例
比如输入的是 "今天早上"
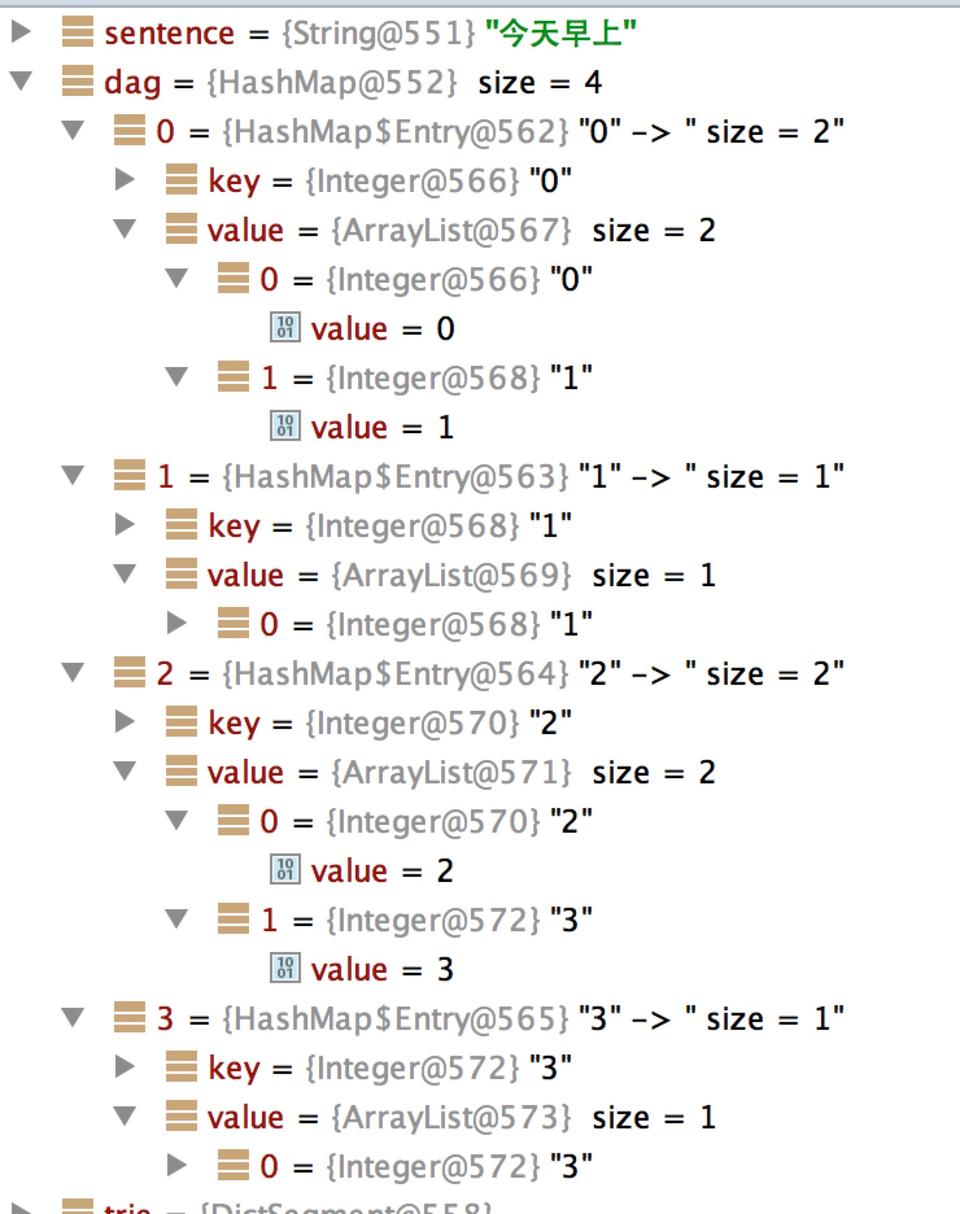
它的DAG展示如下
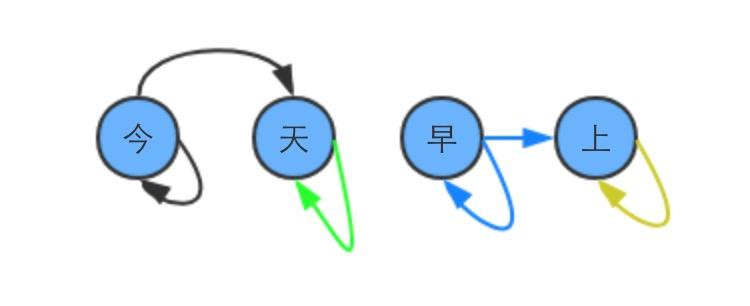
也就是说 "今天早上" 这个句子,在trie中能查到的词为
今/今天/早/早上/上 复制代码
Trie树运用
JieBa内部存储了一个文件dict.txt,比如记录了 X光线 3 n 。在内部的存储trie树结构则为
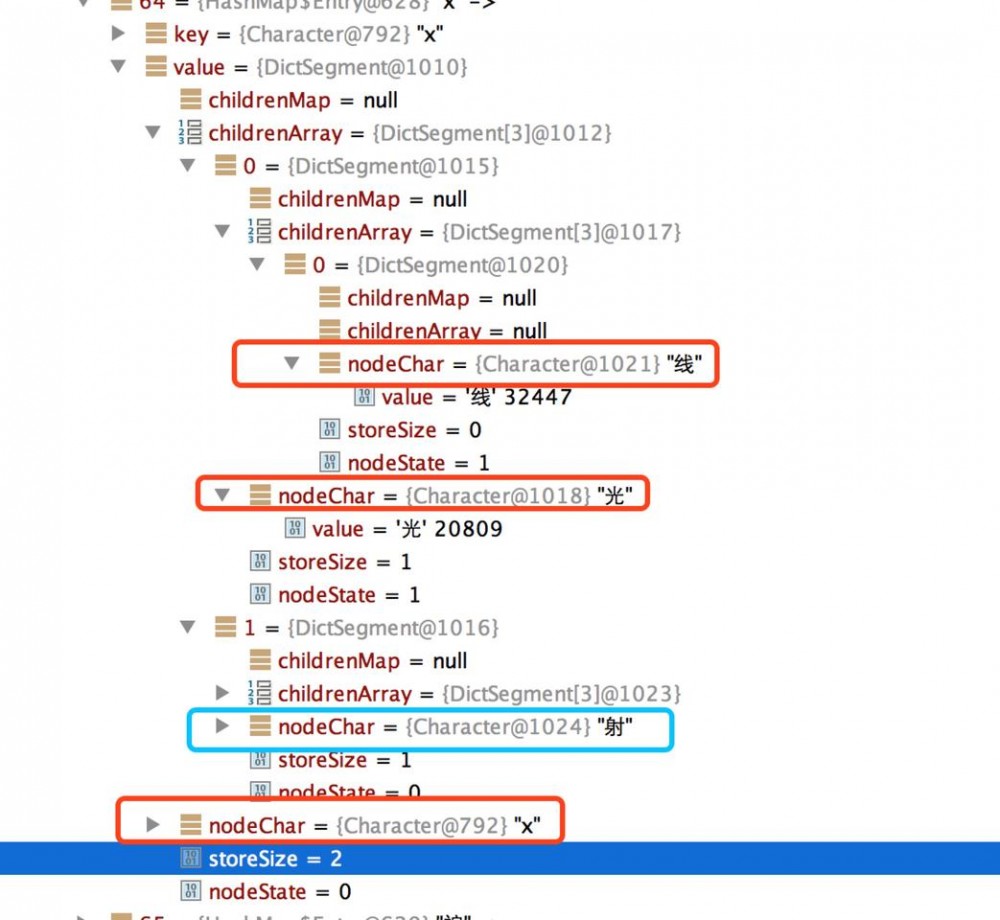
-
nodeState:当前DictSegment状态 ,默认 0 , 1表示从根节点到当前节点的路径表示一个词 ,比如 x光和 x光线
-
storeSize:当前节点存储的Segment数目
比如除了x光线之外,还有x射
- childrenArray和childrenMap用来存储trie树的子节点
storeSize <=ARRAY_LENGTH_LIMIT ,使用数组存储, storeSize >ARRAY_LENGTH_LIMIT,则使用Map存储 ,取值为3
选取高频的词
核心代码如下
for (int i = N - 1; i > -1; i--) {
//从右往左去查看句子,这是因为中文的重点一般在后面
//表示词的开始位置
Pair<Integer> candidate = null;
for (Integer x : dag.get(i)) {
//x表示词的结束位置
// wordDict.getFreq表示获取trie这个词的频率
//route.get(x+1)表示当前词的后一个词的概率
//由于频率本身存储的是数学上log计算后的值,这里的加法其实就是当前这个词为A并且后面紧跟着的词为B的概率,B已经由前面算出
double freq = wordDict.getFreq(sentence.substring(i, x + 1)) + route.get(x + 1).freq;
if (null == candidate) {
candidate = new Pair<Integer>(x, freq);
}
else if (candidate.freq < freq) {
//保存概率高的词
candidate.freq = freq;
candidate.key = x;
}
}
//可见route中存储的数据为key:词头下标 value:词尾下标,词的频率
route.put(i, candidate);
}
复制代码
高频词选取过程:
- i=N-1: route中仅存了一个初始的值,N=4,freq=0,代表最后一个次后面是没有词的,首先获取词 '上' 在trie中的频率为 -5.45,相加后可得上的概率为 -5.45,由于以 '上' 开头的只有1个词,存入route中 <3,-5.45>
(3,<3,-5.45>) :第一个3是词头,第二个3是 '上' 的词尾下标;-5.45是它出现的概率;
(4,<0,0>):初始概率
- i=N-2: 以 '早' 开头的有两个词,分别为 '早' 和 '早上',首先获取词典中 '早' 的频率为 -8.33,它的后一个词为 '上' ,求和后频率为 -13.78;再获取 '早上',在词典中的频率为 -10.81 ,'早上' 后面没有词,因此频率取值就是 -10.81,对比两个词频大小,'早上'的频率大,因此只保留了 '早上'
此时 route保留了 (3,<3,-5.45>)、(4,<0,0>)和(2, <3,-10.81> )
依此类推,经过route之后的取词如下

分词代码
取完了高频词之后,核心逻辑如下
while (x < N) {
//获取当前字符开头的词的词尾
y = route.get(x).key + 1;
String lWord = sentence.substring(x, y);
if (y - x == 1)
sb.append(lWord); //单个字符成词,先保留
else {
if (sb.length() > 0) {
buf = sb.toString();
sb = new StringBuilder();
if (buf.length() == 1) {
tokens.add(buf);
}
else {
if (wordDict.containsWord(buf)) {
tokens.add(buf); //多个字符并且字典中存在,作为分词的结果
}
else {
finalSeg.cut(buf, tokens);
}
}
}
//保留多个字符组成的词
tokens.add(lWord);
}
x = y; //从当前词的词尾开始找下一个词
}
复制代码
词提取的过程
- x=0,找到它的词尾为1,此时获取到了 '今天',由于包含多个词,直接作为分词的结果
- x=2,词尾为3,获取到'早上' ,分词结束
至此 '今天早上' 这句话分词结束。可以看到这都是建立在这个词已经存在于字典的基础上成立的。
如果出现了多个单个字成词的情况,比如 '出门的的时候' 中的 '的',一方面它成为了单个的词,另一方面后面紧跟着的 '的'与它一起成为了两个字符组成的词,又在词典中不存在 '的的' ,因而识别为未知的词,调用 finalSeg.cut
Viterbi算法处理未记录词,重新识别
使用的方法为Viterbi算法。首先预加载如下HMM模型的三组概率集合和隐藏状态集合
-
未知的词定义了4个隐藏状态。 B 表示词的开始 M 表示词的中间 E 表示词的结束 S 表示单字成词
-
初始化每个隐藏状态的初始概率
start.put('B', -0.26268660809250016); start.put('E', -3.14e+100); start.put('M', -3.14e+100); start.put('S', -1.4652633398537678); 复制代码 -
初始化状态转移矩阵
trans = new HashMap<Character, Map<Character, Double>>(); Map<Character, Double> transB = new HashMap<Character, Double>(); transB.put('E', -0.510825623765990); transB.put('M', -0.916290731874155); trans.put('B', transB); Map<Character, Double> transE = new HashMap<Character, Double>(); transE.put('B', -0.5897149736854513); transE.put('S', -0.8085250474669937); trans.put('E', transE); Map<Character, Double> transM = new HashMap<Character, Double>(); transM.put('E', -0.33344856811948514); transM.put('M', -1.2603623820268226); trans.put('M', transM); Map<Character, Double> transS = new HashMap<Character, Double>(); transS.put('B', -0.7211965654669841); transS.put('S', -0.6658631448798212); trans.put('S', transS); 复制代码比如trans.get('S').get('B')表示如果当前字符是 'S',那么下个是另一个词(非单字成词)开始的概率为 -0.721
-
读取实现准备好的混淆矩阵,存入 emit中

红框表示 隐藏状态 'E'的前提下,观察状态是 '要'的概率为 -5.26
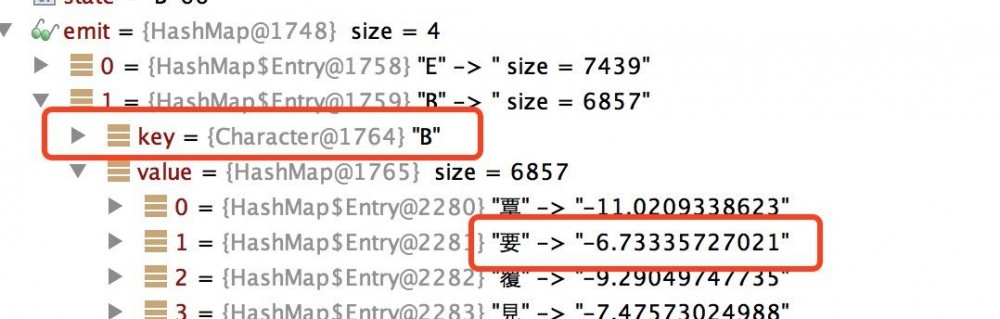
红框表示 隐藏状态 'B'的前提下,观察状态是 '要'的概率为 -6.73
另外它预定义了每个隐藏状态之前只能是那些状态
prevStatus.put('B', new char[] { 'E', 'S' });
prevStatus.put('M', new char[] { 'M', 'B' });
prevStatus.put('S', new char[] { 'S', 'E' });
prevStatus.put('E', new char[] { 'B', 'M' });
复制代码
比如 'M' 它的前面必定是 'M' 和 'B' 之间的一个
算法的流程如下:
- 获取句子中第一个字符在所有隐藏状态下的概率
for (char state : states) { Double emP = emit.get(state).get(sentence.charAt(0)); if (null == emP) emP = MIN_FLOAT; //存储第一个字符 是 'B' 'E' 'M' 'S'的概率,即初始化转移概率 v.get(0).put(state, start.get(state) + emP); path.put(state, new Node(state, null)); } 复制代码 - 计算根据观察序列得到和HMM模型求隐藏序列的概率,并记下最佳解析位置,通过父指针连接起来
for (int i = 1; i < sentence.length(); ++i) {
Map<Character, Double> vv = new HashMap<Character, Double>();
v.add(vv);
Map<Character, Node> newPath = new HashMap<Character, Node>();
for (char y : states) {
//y表示隐藏状态
//emp是获取混淆矩阵的概率,比如 在 'B'发生的情况下,观察到字符 '要' 的概率
Double emp = emit.get(y).get(sentence.charAt(i));
if (emp == null)
emp = MIN_FLOAT; //样本中没有,就设置为最小的概率
Pair<Character> candidate = null;
for (char y0 : prevStatus.get(y)) {
Double tranp = trans.get(y0).get(y);//获取状态转移概率,比如 E -> B
if (null == tranp)
tranp = MIN_FLOAT; //转移概率不存在,取最低的
//v中放的是当前字符的前一个字符的概率,即前一个状态的最优解
//tranp 是状态转移的概率
//三者相加即计算已知观察序列和HMM的条件下,求得最可能的隐藏序列的概率
tranp += (emp + v.get(i - 1).get(y0));
if (null == candidate)
candidate = new Pair<Character>(y0, tranp);
else if (candidate.freq <= tranp) {
//存储最优可能的隐藏概率
candidate.freq = tranp;
candidate.key = y0;
}
}
//存储是'B'还是 'E'各自的概率
vv.put(y, candidate.freq);
//记下前后两个词最优的路径,以便还原原始的隐藏状态分隔点
newPath.put(y, new Node(y, path.get(candidate.key)));
}
//存储最终句子的最优路径
path = newPath;
}
复制代码
- 找到句子尾部的字符的隐藏个状态,并通过最佳路径旅顺整个句子的切割方式
double probE = v.get(sentence.length() - 1).get('E'); double probS = v.get(sentence.length() - 1).get('S'); Vector<Character> posList = new Vector<Character>(sentence.length()); Node win; if (probE < probS) win = path.get('S'); else win = path.get('E'); while (win != null) { //沿着指针找到句子的每个字符的个子位置 posList.add(win.value); win = win.parent; } Collections.reverse(posList); 复制代码 - 遍历这个句子,根据标注,记下所有切割点的词
int begin = 0, next = 0;
for (int i = 0; i < sentence.length(); ++i) {
char pos = posList.get(i);
if (pos == 'B')
begin = i;
else if (pos == 'E') {
//到词尾了,记下
tokens.add(sentence.substring(begin, i + 1));
next = i + 1;
}
else if (pos == 'S') {
//单个字成词,记下
tokens.add(sentence.substring(i, i + 1));
next = i + 1;
}
}
if (next < sentence.length())
tokens.add(sentence.substring(next));
复制代码
自此执行结束
java版 JieBa源码
附录 - HMM学习笔记
马尔科夫假设
假设模型的当前状态仅仅依赖于前面的几个状态,这被称为马尔科夫假设
真实情况当前的状态可能会和前面的状态没有关系,或者有更多的可能性。
比如:预测天气,马尔科夫假设假定今天的天气只能通过过去几天已知的天气情况进行预测——而对于其他因素,譬如风力、气压等则没有考虑。
n阶马尔科夫模型
一个马尔科夫过程是状态间的转移仅依赖于前n个状态的过程。这个过程被称之为n阶马尔科夫模型,其中n是影响下一个状态选择的(前)n个状态
最简单的马尔科夫过程是一阶模型,它的状态选择仅与前一个状态有关。
状态转移概率
从一个状态转移到另一个状态的概率
状态转移矩阵
有M个状态的一阶马尔科夫模型,共有M^2个状态转移,因为任何一个状态都有可能是所有状态的下一个转移状态.所有的M^2个概率可以用一个状态转移矩阵表示
这些概率并不随时间变化而不同——这是一个非常重要(但常常不符合实际)的假设。

也就是说,如果昨天是晴天,那么今天是晴天的概率为0.5,是多云的概率为0.375。注意,每一行的概率之和为1。
一阶马尔科夫过程示例
要初始化这样一个系统,我们需要确定起始日天气的(或可能的)情况,定义其为一个初始概率向量,称为pi向量。

第一天为晴天的概率为1
我们定义一个一阶马尔科夫过程如下:
- 状态:三个状态——晴天,多云,雨天。
- pi向量:定义系统初始化时每一个状态的概率。
- 状态转移矩阵:给定前一天天气情况下的当前天气概率。
任何一个可以用这种方式描述的系统都是一个马尔科夫过程
马尔科夫过程的局限性
无法直接获取要测试的状态的变迁,但是存在一个可以观察的东西,它能够反映要测试的东西的状态变迁,这里要测试的状态变迁为隐藏状态,能够观察的为观察的状态
一个隐士也许不能够直接获取到天气的观察情况,但是他有一些水藻。民间传说告诉我们水藻的状态与天气状态有一定的概率关系——天气和水藻的状态是紧密相关的。希望为隐士设计一种算法,在不能够直接观察天气的情况下,通过水藻和马尔科夫假设来预测天气。
观察到的状态序列与隐藏过程有一定的概率关系。我们使用隐马尔科夫模型对这样的过程建模,这个模型包含了一个底层隐藏的随时间改变的马尔科夫过程,以及一个与隐藏状态某种程度相关的可观察到的状态集合。
隐藏状态和观察状态的关系
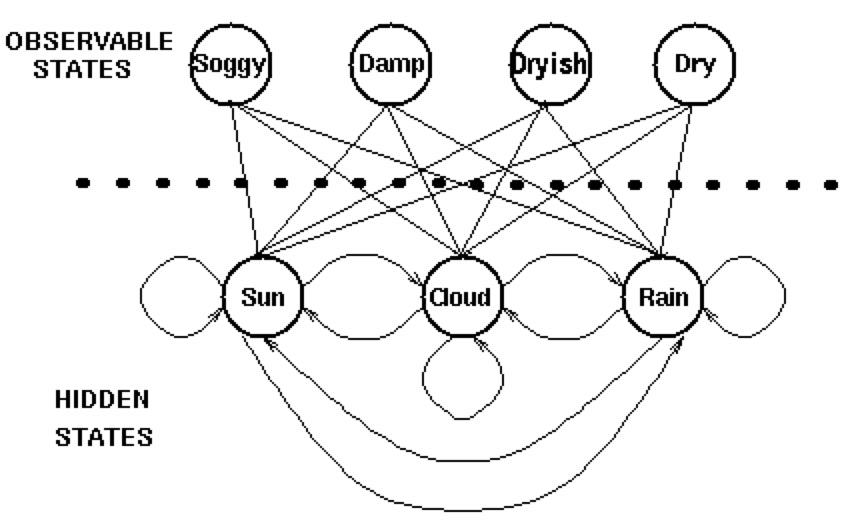
隐藏状态(实际的天气)由一个简单的一阶马尔科夫过程描述
隐藏状态和观察状态之间的连接表示:在给定的马尔科夫过程中,一个特定的隐藏状态生成特定的观察状态的概率,有
Sum_{Obs=Dry,Dryish,Damp,Soggy}(Obs|Sun) = 1;
Sum_{Obs=Dry,Dryish,Damp,Soggy}(Obs|Cloud) = 1;
Sum_{Obs=Dry,Dryish,Damp,Soggy}(Obs|Rain) = 1;
复制代码
混淆矩阵
包含了给定一个隐藏状态后得到的观察状态的概率
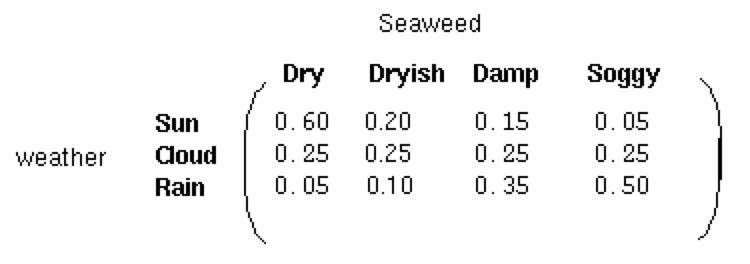
假设是晴天,那么海藻是 干 稍干 潮湿 湿润 的概率分别为 0.6 0.2 0.15 0.05 他们的和为1
隐马尔科夫模型(Hidden Markov Models)
一个隐马尔科夫模型是在一个标准的马尔科夫过程中引入一组观察状态,以及其与隐藏状态间的一些概率关系。
这个模型包含两组状态集合和三组概率集合:
- 隐藏状态:一个系统的(真实)状态,可以由一个马尔科夫过程进行描述(例如,天气)。
- 观察状态:在这个过程中‘可视’的状态(例如,海藻的湿度)。
- pi向量:包含了(隐)模型在时间t=1时一个特殊的隐藏状态的概率(初始概率)
- 状态转移矩阵:包含了一个隐藏状态到另一个隐藏状态的概率
- 混淆矩阵:包含了给定隐马尔科夫模型的某一个特殊的隐藏状态,观察到的某个观察状态的概率。
观察状态的数目可以和隐藏状态的数码不同。
HMM定义
一个隐马尔科夫模型是一个三元组(pi, A, B)
- :初始化概率矩阵
- :状态转移矩阵,
- :混淆矩阵,
在状态转移矩阵及混淆矩阵中的每一个概率都是时间无关的——也就是说,当系统演化时这些矩阵并不随时间改变
这是马尔科夫模型关于真实世界最不现实的一个假设。
应用
-
模式识别:
-
给定HMM求一个观察序列的概率(评估)
-
搜索最有可能生成一个观察序列的隐藏状态序列(解码)
-
-
给定观察序列生成一个HMM(学习)
评估
有一些描述不同系统的隐马尔科夫模型(也就是一些( pi,A,B)三元组的集合)及一个观察序列。我们想知道哪一个HMM最有可能产生了这个给定的观察序列。
对于海藻来说,我们也许会有一个“夏季”模型和一个“冬季”模型,因为不同季节之间的情况是不同的——我们也许想根据海藻湿度的观察序列来确定当前的季节。
使用前向算法(forward algorithm)来计算给定隐马尔科夫模型(HMM)后的一个观察序列的概率,并因此选择最合适的隐马尔科夫模型(HMM)。
解码
在许多情况下我们对于模型中的隐藏状态更感兴趣,因为它们代表了一些更有价值的东西,而这些东西通常不能直接观察到。
一个盲人隐士只能感觉到海藻的状态,但是他更想知道天气的情况,天气状态在这里就是隐藏状态。
使用Viterbi 算法(Viterbi algorithm)确定(搜索)已知观察序列及HMM下最可能的隐藏状态序列。
学习
根据一个观察序列(来自于已知的集合),以及与其有关的一个隐藏状态集,估计一个最合适的隐马尔科夫模型(HMM),也就是确定对已知序列描述的最合适的(pi,A,B)三元组。
当矩阵A和B不能够直接被(估计)测量时,前向-后向算法(forward-backward algorithm)被用来进行学习(参数估计)
前向算法
-
穷举搜索
我们有一个用来描述天气及与它密切相关的海藻湿度状态的隐马尔科夫模型(HMM),另外我们还有一个海藻的湿度状态观察序列。假设连续3天海藻湿度的观察结果是(干燥、湿润、湿透)——而这三天每一天都可能是晴天、多云或下雨。
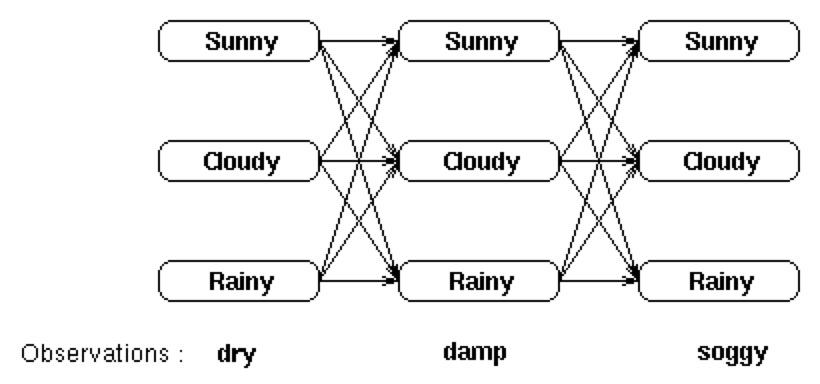
每一列都显示了可能的的天气状态,并且每一列中的每个状态都与相邻列中的每一个状态相连。而其状态间的转移都由状态转移矩阵提供一个概率。
在每一列下面都是某个时间点上的观察状态,给定任一个隐藏状态所得到的观察状态的概率由混淆矩阵提供。
现在要计算当前HMM能够得到观察序列是 dry,damp,soggy 的概率。
找到每一个可能的隐藏状态,并且将这些隐藏状态下的观察序列概率相加,也就是穷举所有的隐藏概率发生的情况下,是现有观察状态的概率
Pr(dry,damp,soggy | HMM) = Pr(dry,damp,soggy | sunny,sunny,sunny) + Pr(dry,damp,soggy | sunny,sunny ,cloudy) + Pr(dry,damp,soggy | sunny,sunny ,rainy) + . . . . Pr(dry,damp,soggy | rainy,rainy ,rainy) 复制代码
用到的是当前的HMM
缺点:计算观察序列概率极为昂贵,特别对于大的模型或较长的序列
应用:利用概率的时间不变性来减少问题的复杂度。
-
递归降低问题复杂度【动态规划思想】
计算过程中将计算到达网格中某个中间状态的概率作为所有到达这个状态的可能路径的概率求和问题。
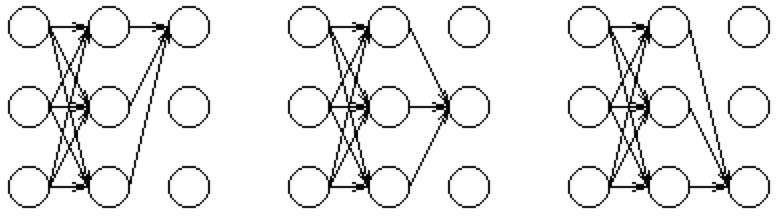
同样对于穷举的计算方法,可以拆分成多个从当前状态转移到下一个局部状态,再把所有的局部状态求和就得到定隐马尔科夫模型(HMM)后的观察序列概率。概率为
αt ( j )= Pr( 观察状态 | 隐藏状态j ) x Pr(t时刻所有指向j状态的路径) 复制代码
j 表示局部状态;αt ( j )表示处于这个状态的概率;t表示时间;Pr( 观察状态 | 隐藏状态j )即混淆矩阵;Pr(t时刻所有指向j状态的路径)即状态转移矩阵
-
当t=1时,没有任何指向当前状态的路径。故t=1时位于当前状态的概率是初始概率,因此,t=1时的局部概率等于当前状态的初始概率乘以相关的观察概率
-
计算t>1的局部概率 α
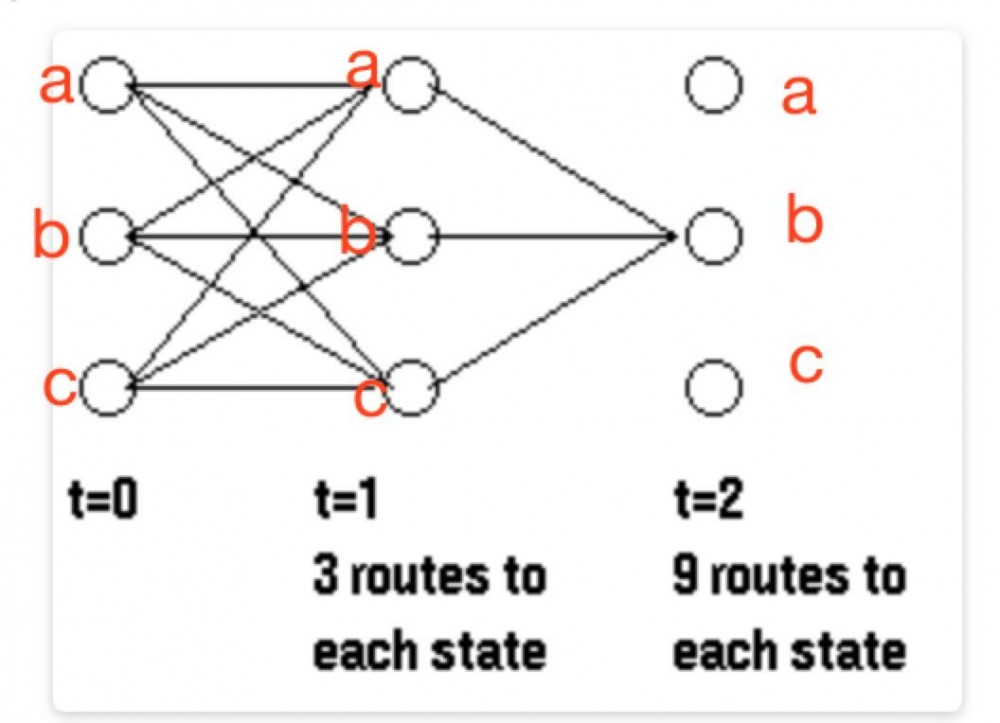
要计算t=2时,局部状态为b的概率,必须要计算所有 t=1时刻,从a,b,c到t=2时状态为b的概率,而要得到t=1时刻的所有概率,已经在前一步从t=0运转到t=1的时候计算过了。
也就是说 t=2时,观察序列前提下,局部隐藏状态为b的概率为t=1状态所有的概率和再乘以混淆矩阵转移到当前观察变量的概率。即
-
维特比算法(Viterbi Algorithm)
对于一个特殊的隐马尔科夫模型(HMM)及一个相应的观察序列,我们常常希望能找到生成此序列最可能的隐藏状态序列
-
穷举搜索
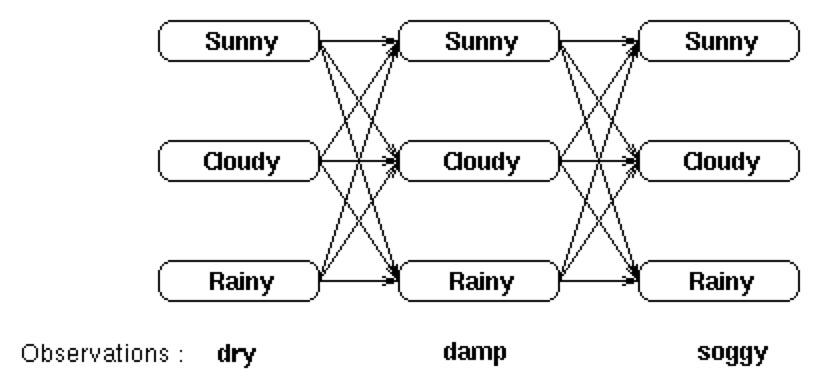
对于网格中所显示的观察序列,最可能的隐藏状态序列是下面这些概率中最大概率所对应的那个隐藏状态序列:
Pr(dry,damp,soggy | sunny,sunny,sunny), Pr(dry,damp,soggy | sunny,sunny,cloudy), Pr(dry,damp,soggy | sunny,sunny,rainy), . . . . Pr(dry,damp,soggy | rainy,rainy,rainy) 复制代码
但是太昂贵了
-
递归降低复杂度
定义局部概率,它是到达网格中的某个特殊的中间状态时的概率
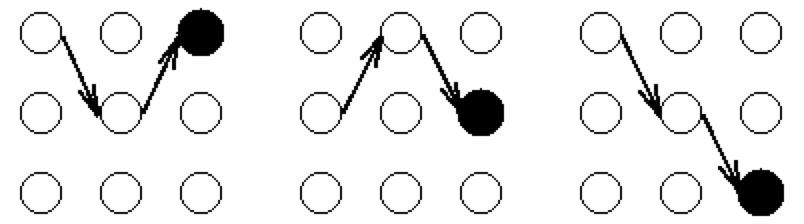
对于网格中的每一个中间及终止状态,都有一个到达该状态的最可能路径。称这些路径局部最佳路径(partial best paths)。其中每个局部最佳路径都有一个相关联的概率,即局部概率或
与前向算法中的局部概率不同,是到达该状态(最可能)的一条路径的概率。
因而(i,t)是t时刻到达状态i的所有序列概率中最大的概率, 特别地,在t=T时每一个状态都有一个局部概率和一个局部最佳路径。这样我们就可以通过选择此时刻包含最大局部概率的状态及其相应的局部最佳路径来确定全局最佳路径(最佳隐藏状态序列)。
- 当t=1的时候,到达某状态的最可能路径明显是不存在的;但是,我们使用t=1时的所处状态的初始概率及相应的观察状态k1的观察概率计算局部概率
- 考虑计算t时刻到达状态X的最可能的路径;这条到达状态X的路径将通过t-1时刻的状态A,B或C中的某一个。因此,最可能的到达状态X的路径将是下面这些路径的某一个
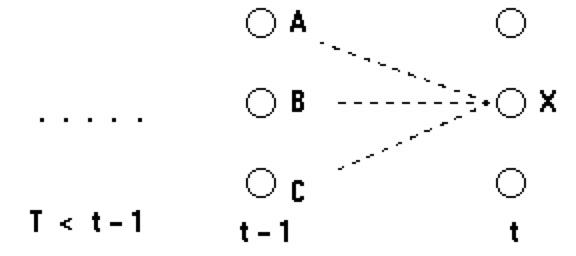
(状态序列),...,A,X (状态序列),...,B,X (状态序列),...,C,X 复制代码
路径末端是AX的最可能的路径将是到达A的最可能路径再紧跟X。这条路径的概率将是:
   Pr (到达状态A最可能的路径) .Pr (X | A) . Pr (观察状态 | X)马尔科夫假设:给定一个状态序列,一个状态发生的概率只依赖于前n个状态。特别地,在一阶马尔可夫假设下,状态X在一个状态序列后发生的概率只取决于之前的一个状态
因此,到达状态X的最可能路径概率是
这里,我们假设前一个状态的知识(局部概率)是已知的,同时利用了状态转移概率和相应的观察概率之积。然后,我们就可以在其中选择最大的概率了(局部概率 )
反向指针
目标是在给定一个观察序列的情况下寻找网格中最可能的隐藏状态序列——因此,我们需要一些方法来记住网格中的局部最佳路径。
计算t时刻的's我们仅仅需要知道t-1时刻的's。在这个局部概率计算之后,就有可能记录前一时刻哪个状态生成了(i,t)——也就是说,在t-1时刻系统必须处于某个状态,该状态导致了系统在t时刻到达状态i是最优的。这种记录(记忆)是通过对每一个状态赋予一个反向指针完成的,这个指针指向最优的引发当前状态的前一时刻的某个状态。
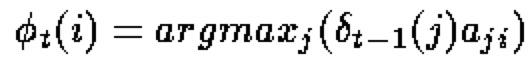
其中argmax运算符是用来计算使括号中表达式的值最大的索引j的。










![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)

