HashMap之元素删除
微信公众号:如有问题或建议,请在下方留言;
最近更新:2018-09-18
HashMap之元素删除
继上一篇HashMap之元素插入,我们继续来看下元素删除的实现原理。
1、源码:
1public V remove(Object key) {
2 Node<K,V> e;
3 return (e = removeNode(hash(key), key, null, false, true)) == null ?
4 null : e.value;
5}
复制代码
看下核心方法removeNode:
1//matchValue为false 表示不需要比对value值一致
2//movable为false 表示删除节点后不移动其他节点
3final Node<K,V> removeNode(int hash, Object key, Object value,
4 boolean matchValue, boolean movable) {
5 //p为当前检查的节点
6 Node<K,V>[] tab; Node<K,V> p; int n, index;
7 if ((tab = table) != null && (n = tab.length) > 0 &&
8 (p = tab[index = (n - 1) & hash]) != null) { //待删除节点在数组索引位置存在元素
9 //node为找到的删除节点
10 Node<K,V> node = null, e; K k; V v;
11 if (p.hash == hash &&
12 ((k = p.key) == key || (key != null && key.equals(k))))//哈希值一致,key一致则找到了要删除的节点
13 node = p;
14 else if ((e = p.next) != null) {//未找到则看后继节点
15 if (p instanceof TreeNode)//如果后继节点为红黑树节点,则在红黑树中查找要删除的节点
16 node = ((TreeNode<K,V>)p).getTreeNode(hash, key);
17 else {
18 do {
19 if (e.hash == hash &&
20 ((k = e.key) == key ||
21 (key != null && key.equals(k)))) {
22 node = e;
23 break;
24 }
25 p = e;
26 } while ((e = e.next) != null);//不为红黑树节点,则遍历单链表查找
27 }
28 }
29 if (node != null && (!matchValue || (v = node.value) == value ||
30 (value != null && value.equals(v)))) {//找到节点,matchValue为true,还需要比对value值
31 if (node instanceof TreeNode)
32 ((TreeNode<K,V>)node).removeTreeNode(this, tab, movable);//待删除节点为红黑树节点,则进行红黑树节点的删除操作
33 else if (node == p)//待删除节点为数组中的元素,直接将后继节点替换即可
34 tab[index] = node.next;
35 else//待删除节点为单链表中的元素,将后继节点作为前驱节点的后继节点即可
36 p.next = node.next;
37 ++modCount;
38 --size;
39 afterNodeRemoval(node);
40 return node;
41 }
42 }
43 return null;
44}
复制代码
2、流程图:

3、说明:
因为HashMap存在三种存储方式,数组、单链表、红黑树,那么删除元素时必然存在着这三种情况。其中,红黑树的删除最为复杂,咱们接着往下看。
红黑树之查找元素
1、源码:
1final TreeNode<K,V> getTreeNode(int h, Object k) {
2 return ((parent != null) ? root() : this).find(h, k, null);
3}
4
5//查找红黑树的根节点
6final TreeNode<K,V> root() {
7 for (TreeNode<K,V> r = this, p;;) {
8 if ((p = r.parent) == null)
9 return r;
10 r = p;
11 }
12}
13
14//遍历红黑树查找指定哈希和key的节点
15final TreeNode<K,V> find(int h, Object k, Class<?> kc) {
16 TreeNode<K,V> p = this;
17 do {
18 int ph, dir; K pk;
19 TreeNode<K,V> pl = p.left, pr = p.right, q;//保存左节点 右节点
20 if ((ph = p.hash) > h) //左节点哈希值大于给定查找节点的哈希值,则继续往左找
21 p = pl;
22 else if (ph < h)//左节点哈希值小于给定查找节点的哈希值,则往右找
23 p = pr;
24 else if ((pk = p.key) == k || (k != null && k.equals(pk)))//当前节点key值一致,则返回该节点
25 return p;
26 else if (pl == null)//左节点为空,则往右找
27 p = pr;
28 else if (pr == null)//右节点为空,则往左找
29 p = pl;
30 else if ((kc != null ||//哈希相同,key不同,且有左右节点。此时看key是否可比较,是则比较key值
31 (kc = comparableClassFor(k)) != null) &&
32 (dir = compareComparables(kc, k, pk)) != 0)
33 p = (dir < 0) ? pl : pr;//小于往左,大于往右
34 else if ((q = pr.find(h, k, kc)) != null)//哈希相同,key不可比或者key也相同,则往右查找
35 return q;
36 else//否则往左
37 p = pl;
38 } while (p != null);
39 return null;
40}
复制代码
2、流程图:
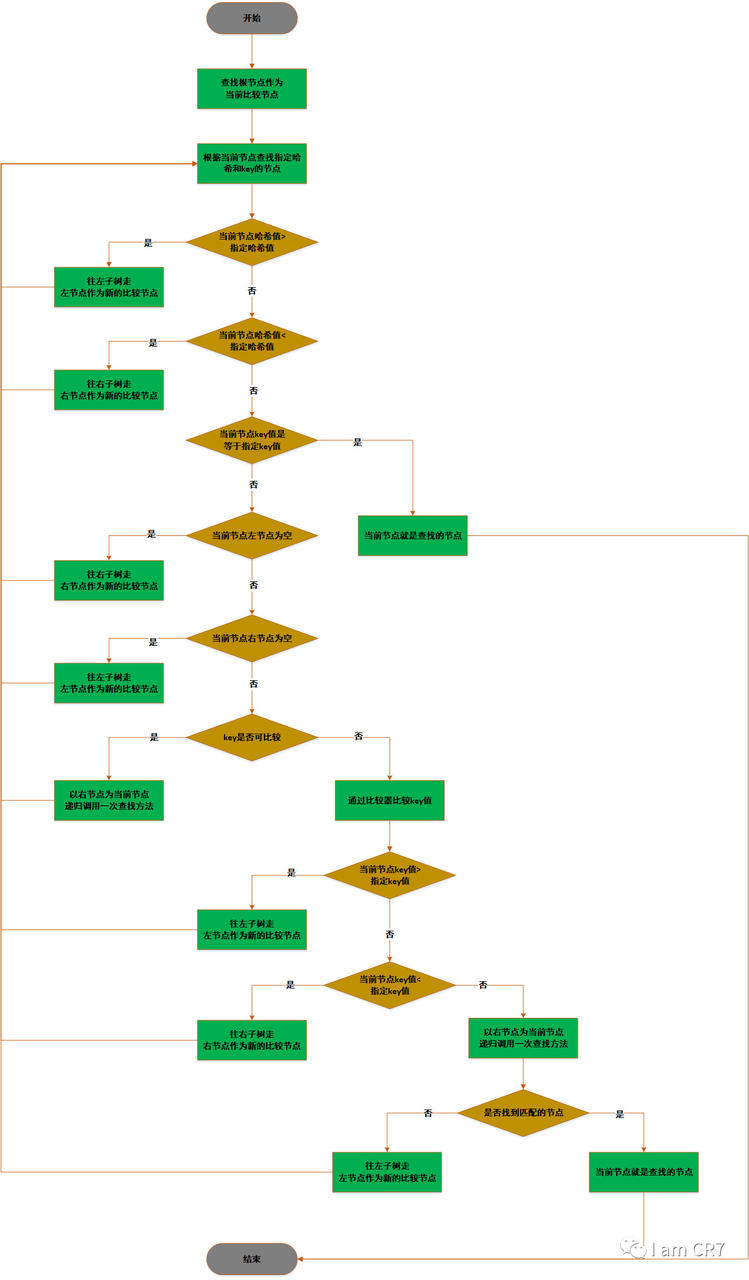
红黑树之删除元素
1、源码:
1final void removeTreeNode(HashMap<K,V> map, Node<K,V>[] tab,
2 boolean movable) {
3 int n;
4 if (tab == null || (n = tab.length) == 0)
5 return;
6 int index = (n - 1) & hash;
7 TreeNode<K,V> first = (TreeNode<K,V>)tab[index], root = first, rl;
8 TreeNode<K,V> succ = (TreeNode<K,V>)next, pred = prev;
9 if (pred == null) //待删除节点为根节点,则其后继节点作为数组索引位置的元素
10 tab[index] = first = succ;
11 else//待删除节点存在前驱节点,则后继节点作为前驱节点的下一个节点
12 pred.next = succ;
13 if (succ != null)//待删除节点存在后继节点,则前驱节点作为后继节点的上一个节点
14 succ.prev = pred;
15 if (first == null)//数组索引位置元素为null,直接返回
16 return;
17 if (root.parent != null)//找到红黑树的根节点
18 root = root.root();
19 if (root == null || root.right == null ||
20 (rl = root.left) == null || rl.left == null) {//红黑树太小则进行去树化操作
21 tab[index] = first.untreeify(map); // too small
22 return;
23 }
24 //查找替代节点replacement
25 //p为待删除节点,pl为其左节点,pr为其右节点,replacement为替代节点
26 TreeNode<K,V> p = this, pl = left, pr = right, replacement;
27 if (pl != null && pr != null) {//待删除节点有左右节点
28 //s为后继节点
29TreeNode<K,V> s = pr, sl;
30 while ((sl = s.left) != null)//往待删除节点右子树的左边走
31 s = sl;
32 boolean c = s.red; s.red = p.red; p.red = c;//互换后继节点和待删除节点的颜色
33 //sr为后继节点的右节点
34 TreeNode<K,V> sr = s.right;
35 //pp为待删除节点的父节点
36 TreeNode<K,V> pp = p.parent;
37 if (s == pr) {//待删除节点的右节点无左孩子--->右节点和待删除节点互换
38 p.parent = s;
39 s.right = p;
40 }
41 else {//待删除节点的右节点有左孩子
42 //sp为后继节点的父节点
43 TreeNode<K,V> sp = s.parent;
44 //后继节点存在父节点,则让待删除节点替代后继节点
45 if ((p.parent = sp) != null) {//后继节点的父节点成为待删除节点的父节点
46 if (s == sp.left)//后继节点为其父节点的左孩子
47 sp.left = p;//待删除节点就作为后继节点的父节点的左孩子
48 else
49 sp.right = p;//待删除节点就作为后继节点的父节点的右孩子
50 }
51 //待删除节点存在右节点,则让后继节点成为其父节点
52 if ((s.right = pr) != null)
53 pr.parent = s;
54 }
55 p.left = null;//待删除节点左孩子为null
56 if ((p.right = sr) != null)//后继节点存在右节点,则让其成为待删除节点的右节点
57 sr.parent = p;//相对应,待删除节点成为其父节点
58 if ((s.left = pl) != null)//待删除节点存在左节点,则让其成为后继节点的左节点
59 pl.parent = s;//相对应,后继节点成为其父节点
60 //待删除节点存在父节点,则让后继节点替代待删除节点
61 if ((s.parent = pp) == null)//待删除节点不存在父节点,则后继节点父节点为null
62 root = s;//后继节点成为根节点
63 else if (p == pp.left)//待删除节点存在父节点,且待删除节点是其左节点
64 pp.left = s;//后继节点作为其左节点
65 else
66 pp.right = s;//后继节点作为其右节点
67 //后继节点存在右节点,则替代节点为该节点
68 if (sr != null)
69 replacement = sr;
70 else //替代节点为待删除节点(等于未找到)
71 replacement = p;
72 }
73 else if (pl != null)//待删除节点只有左节点
74 replacement = pl;
75 else if (pr != null)//待删除节点只有右节点
76 replacement = pr;
77 else//待删除节点为叶子节点
78 replacement = p;
79 if (replacement != p) {//替代节点不为待删除节点,则先进行节点删除,然后进行平衡调整
80 TreeNode<K,V> pp = replacement.parent = p.parent;
81 if (pp == null)
82 root = replacement;
83 else if (p == pp.left)
84 pp.left = replacement;
85 else
86 pp.right = replacement;
87 p.left = p.right = p.parent = null;
88 }
89
90 TreeNode<K,V> r = p.red ? root : balanceDeletion(root, replacement);//进行平衡调整
91
92 if (replacement == p) { //替代节点为待删除节点,则先进行平衡调整,然后进行节点删除
93 TreeNode<K,V> pp = p.parent;
94 p.parent = null;
95 if (pp != null) {
96 if (p == pp.left)
97 pp.left = null;
98 else if (p == pp.right)
99 pp.right = null;
100 }
101 }
102 if (movable)//将红黑树根节点移动到数组索引位置
103 moveRootToFront(tab, r);
104}
复制代码
2、流程图:
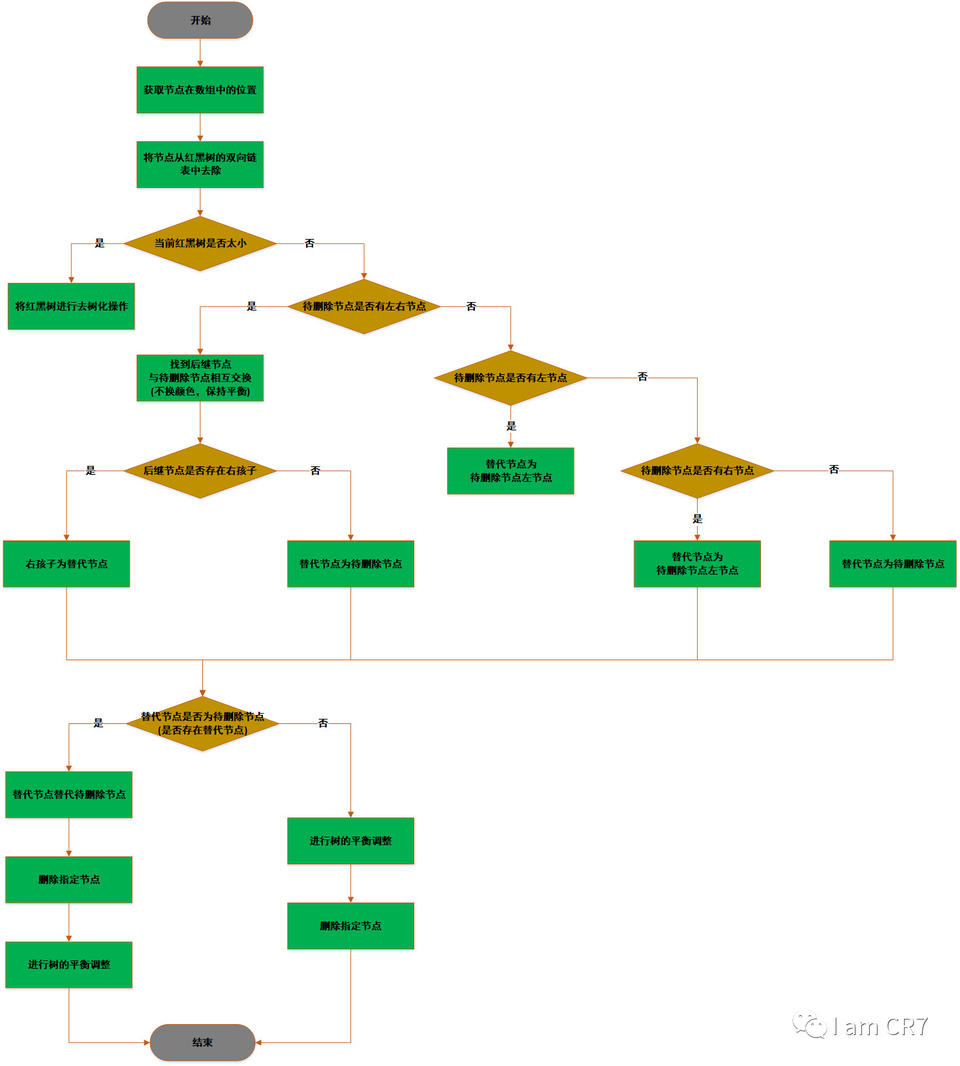
3、说明:
以上为HashMap的红黑树删除流程,其实思路和TreeMap中红黑树大致相同,关于TreeMap的解析,请看TreeMap之元素删除,文章中我对红黑树的删除过程进行了详细的分析,这里就不做详细阐述了。
示例
我们通过一个具体的例子,来体会下删除的过程,请看:
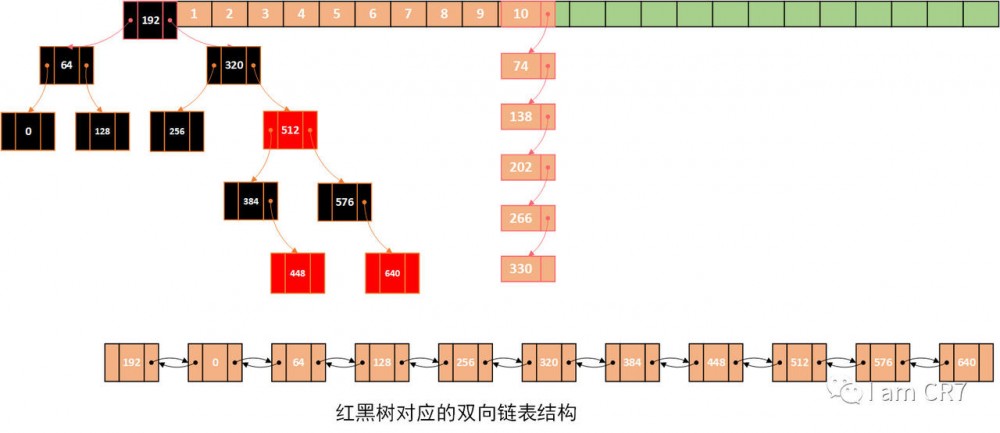
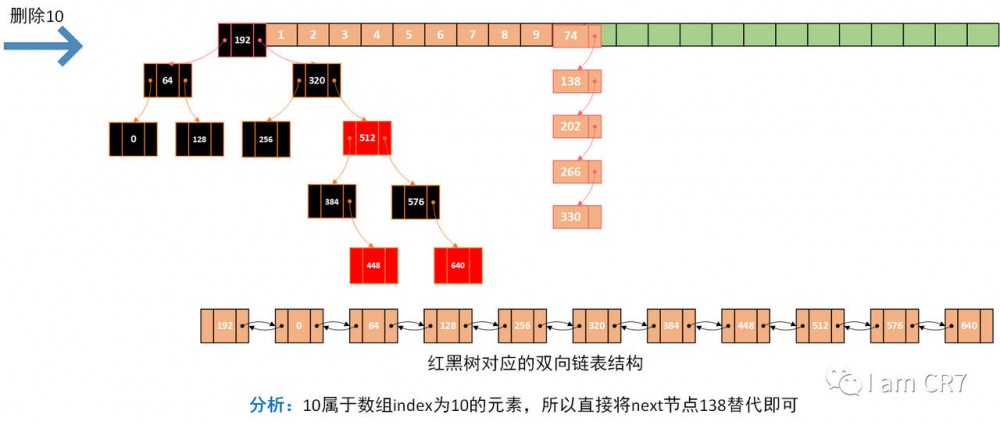
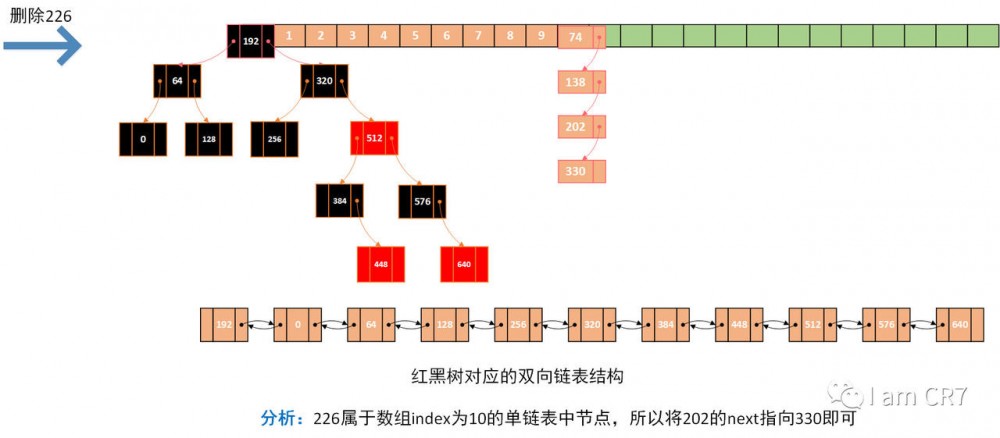
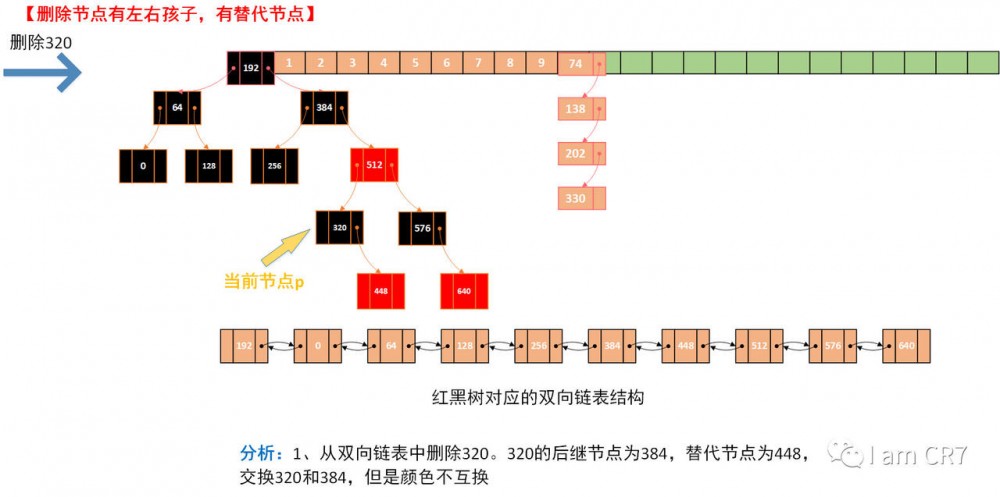
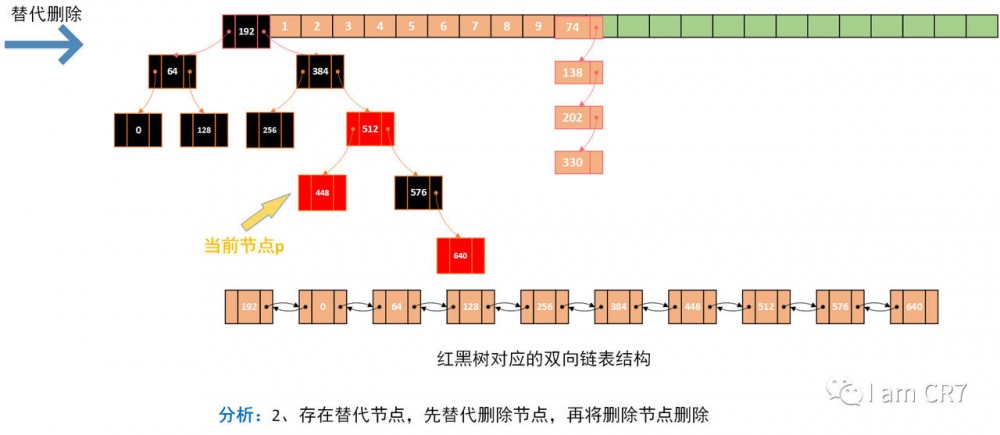
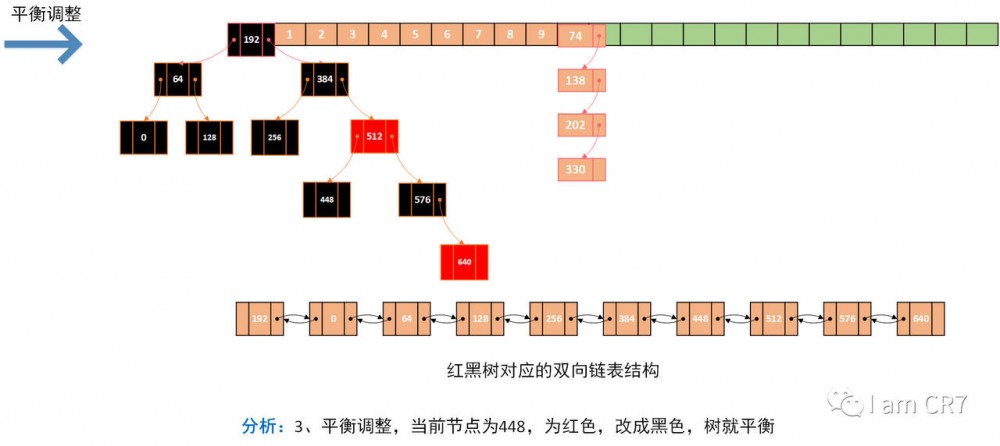
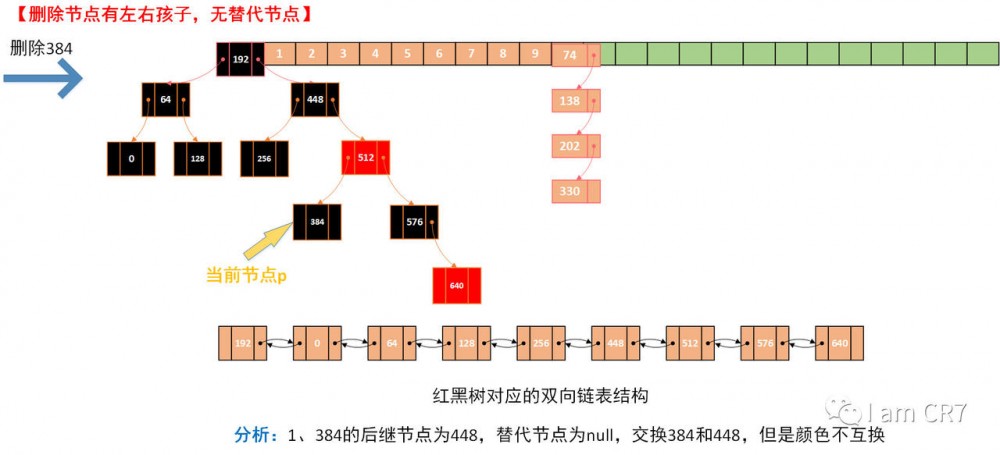
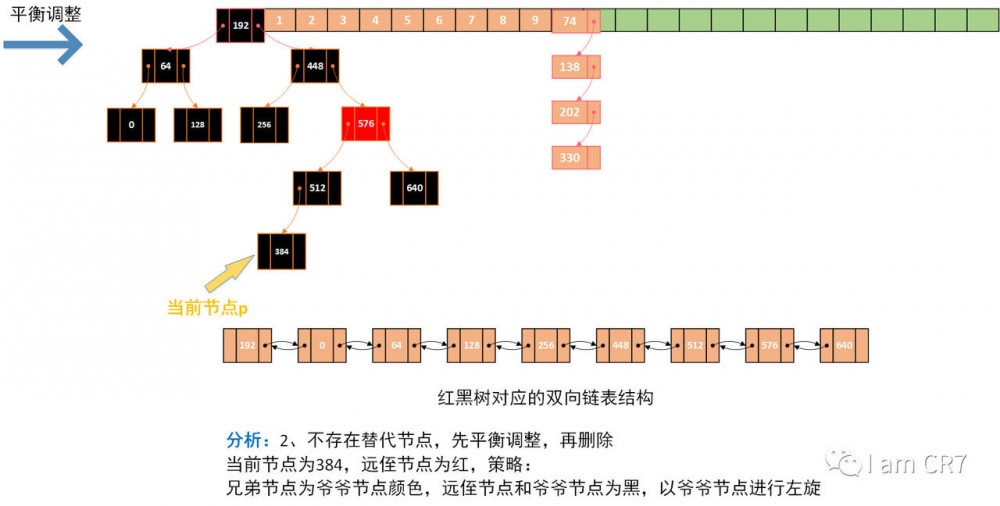
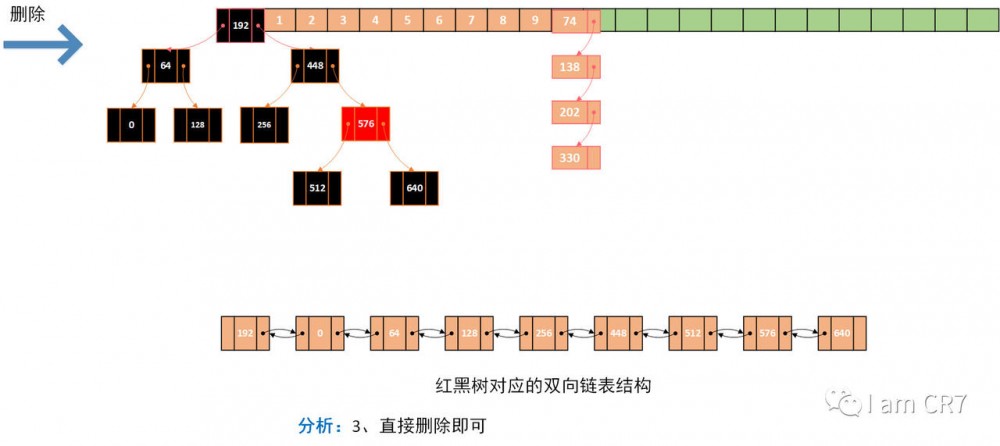
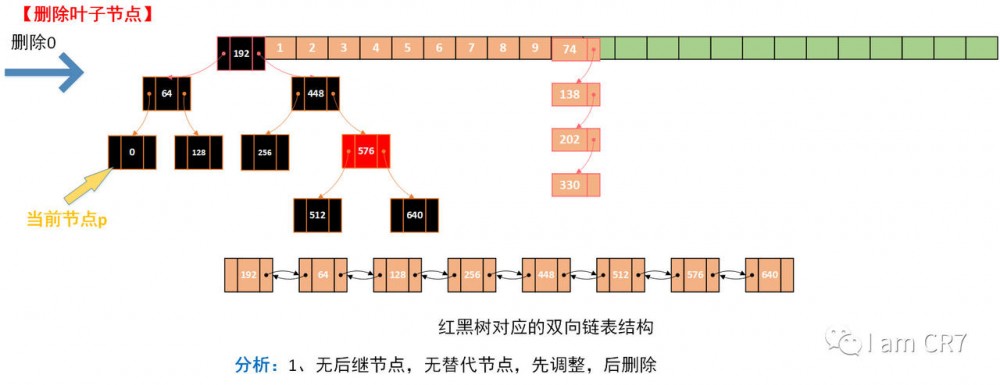
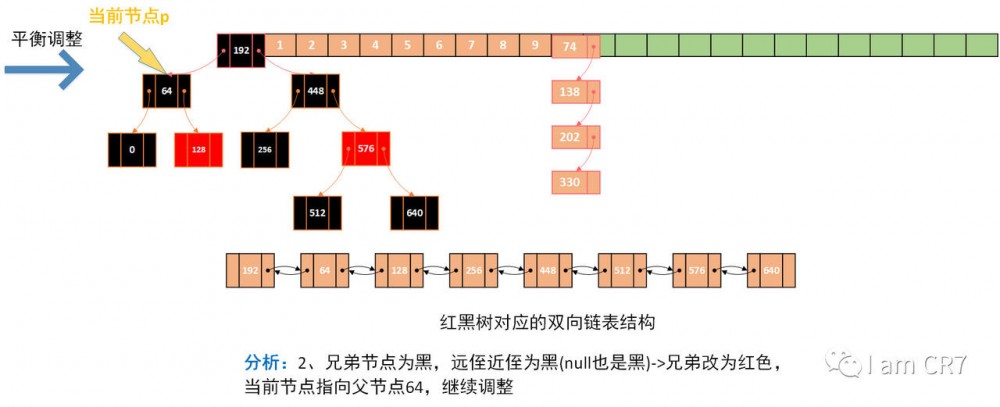
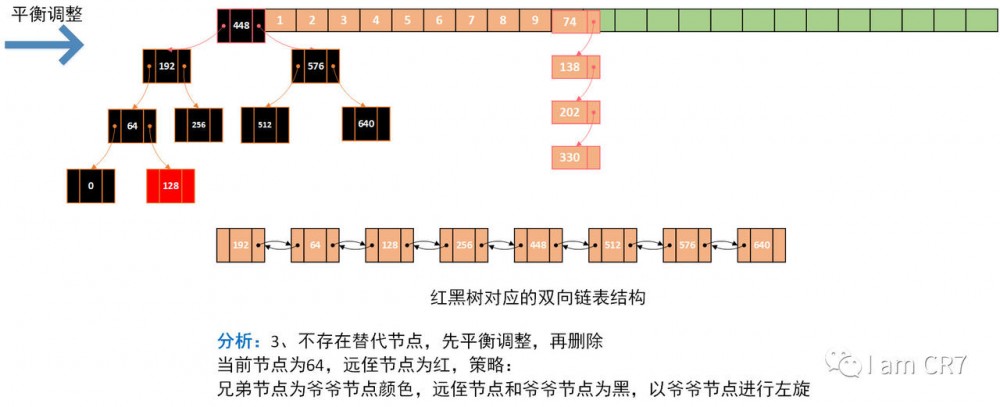
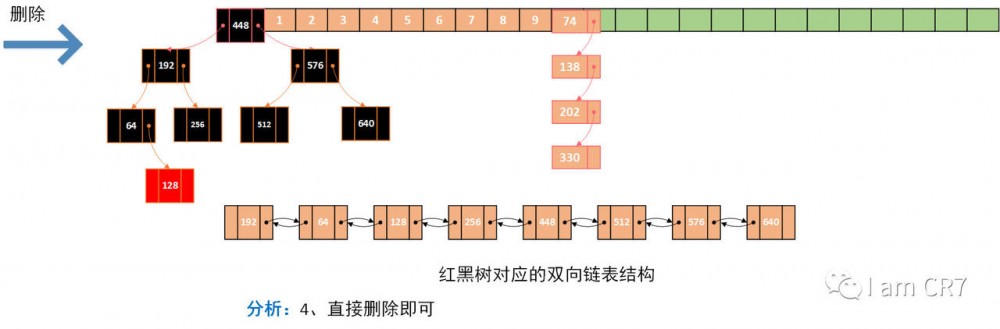
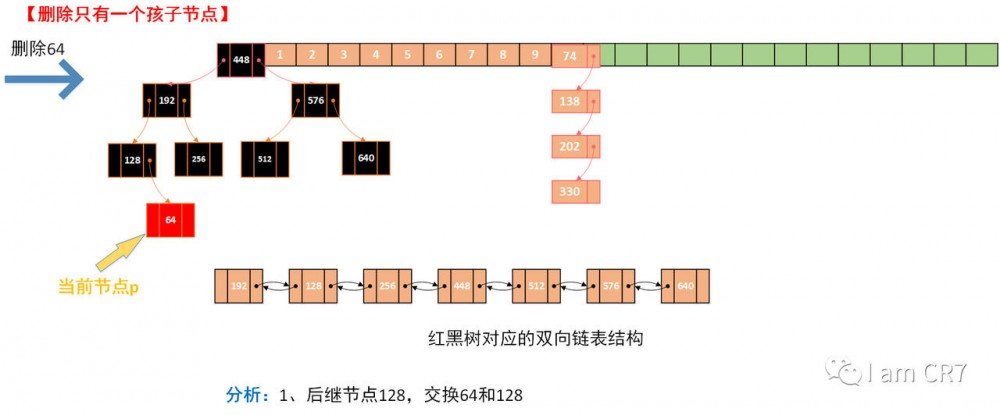
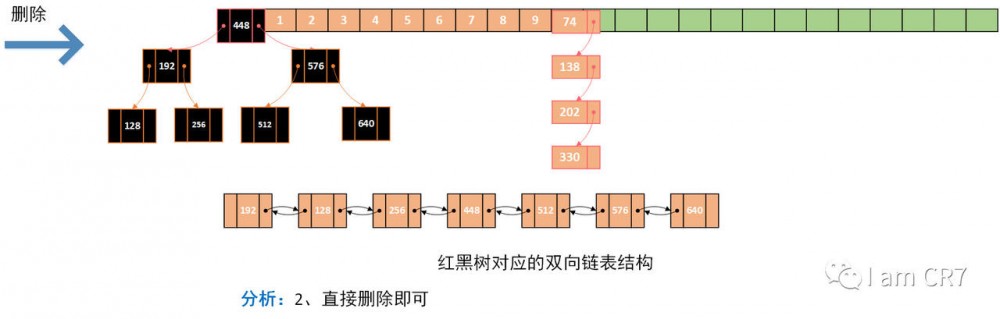
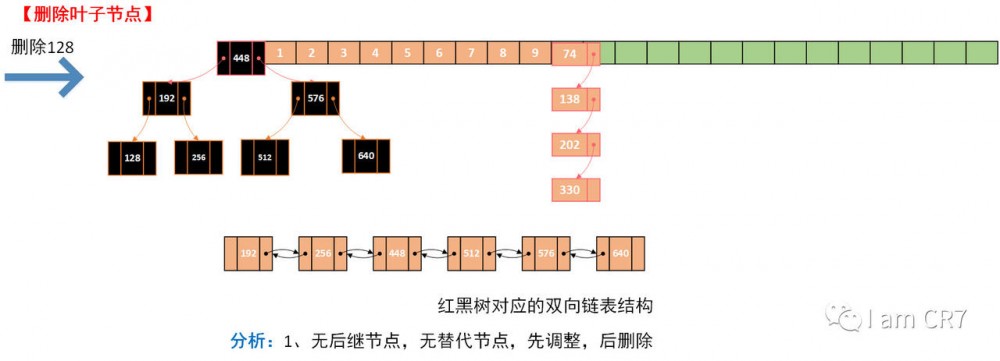
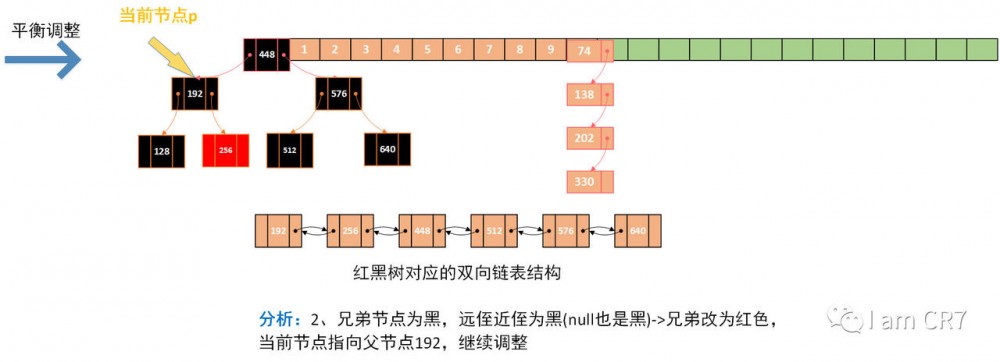
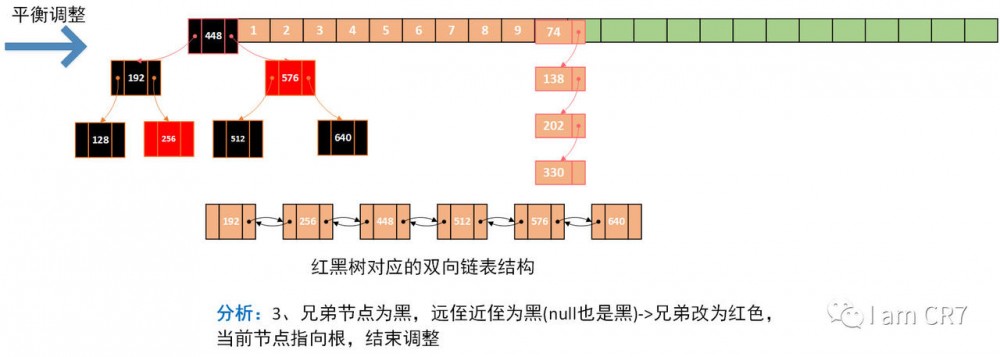
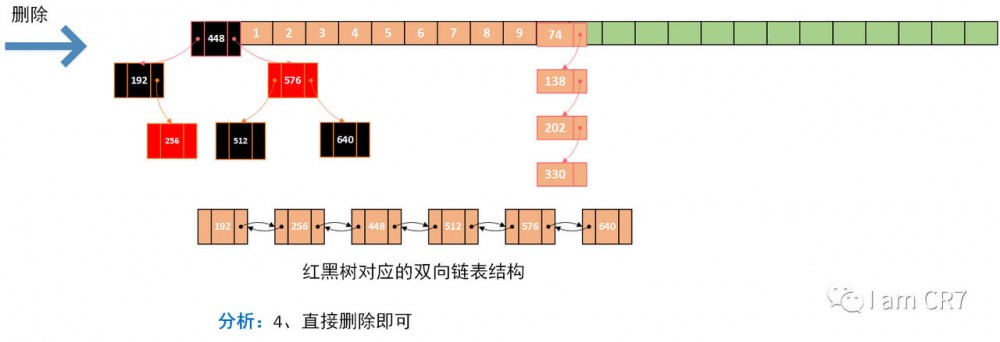
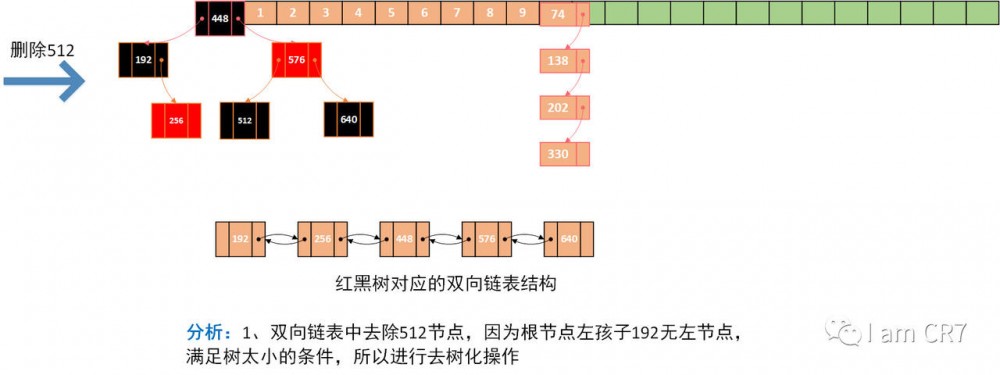
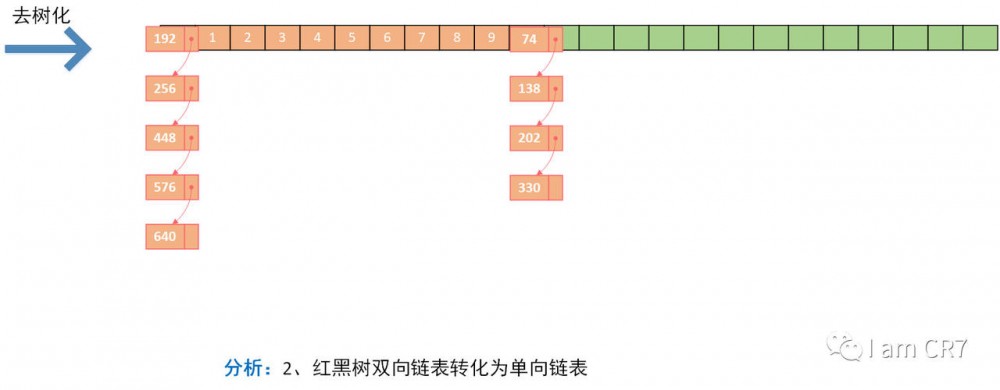
总结
通过上述的分析,结合着TreeMap之元素删除这篇文章,我想,要理解HashMap的删除,并不是一件难事。
文章的最后,感谢大家的支持,欢迎扫描下方二维码,进行关注。如有任何疑问,欢迎大家留言。
正文到此结束
热门推荐
相关文章
Loading...











![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)

