转载

模型的泛化能力仅和Hessian谱有关吗？

Salesforce 近日提出了一篇探究模型泛化能力的论文，他们在 PAC-Bayes 框架下将解的平滑性和模型的泛化能力联系在了一起，并从理论上证明了模型的泛化能力不仅和 Hessian 谱有关，和解的平滑性、参数的尺度以及训练样本的数量也有关。

经验表明，通过训练深度神经网络得到的不同局部最优值往往并不能以相同的方式泛化到未知数据集上，即使取得了相同的训练损失。近年来，这一问题日益受到经验和理论深度学习研究社区的关注。从理论的角度来看，大多数用来解释这种现象的泛化边界只考虑了最差的情况，因此忽略了不同解的泛化能力。在本文中，我们将重点探讨下面的问题：

解的局部「平滑性」和模型的泛化能力有何关系？

对 Hessian 二阶导数和泛化能力的经验观测结果

从较早的 Hochreiter 和 Schmidhuber 等人的论文《FLAT MINIMA》到最近的 Chaudhari《Entropy-SGD: Biasing Gradient Descent Into Wide Valleys》和 Keskar《On Large-Batch Training for Deep Learning: Generalization Gap and Sharp Minima》等人的研究都认为，深度学习收敛解的局部曲率（或称「锐度」）与由此得到的分类器的泛化性质密切相关。「尖锐」的最小值（二阶导很大）会导致模型缺乏泛化能力，我们通过大量的中的大和正的特征值来刻画它，在这一点损失函数最小。

Neyshabur 等人《Exploring Generalization in Deep Learning》指出，锐度本身可能并不足以决定泛化能力。他们认为，解的尺度（如 norm、margin）和锐度会同时影响泛化能力。为此，他们提出了一个基于 PAC-贝叶斯边界的「期望锐度」：

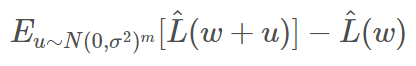
模型的泛化能力仅和Hessian谱有关吗？

如下图所示，如果局部最小值是「平滑的」，那么对模型的干扰不会导致目标函数发生太大的变化。因此，它提供了一种测量局部最小值平滑度的方法。

模型的泛化能力仅和Hessian谱有关吗？

如何扰动模型？

众所周知，在训练中给模型添加噪声有助于提高模型的泛化能力。然而，如何设置合适的噪声水平仍然是个有待解决的问题。目前大多数最先进的方法假设在所有的方向上都有相同程度的扰动，但是直觉告诉我们这样做可能并不合适。

举一个简单的例子来看，我们用 k=3 的高斯混合模型构建了一个小的二维样本集，并通过将标签以中值为阈值二值化。然后采用 5 层仅仅带有 w_1、w_2 两个参数的多层感知机进行预测，使用交叉熵作为损失函数。不同层的变量会被共享。在这里我们采用 sigmoid 作为激励函数。下图为使用 100 个样本训练出的模型的损失函数的变化情况示意图：

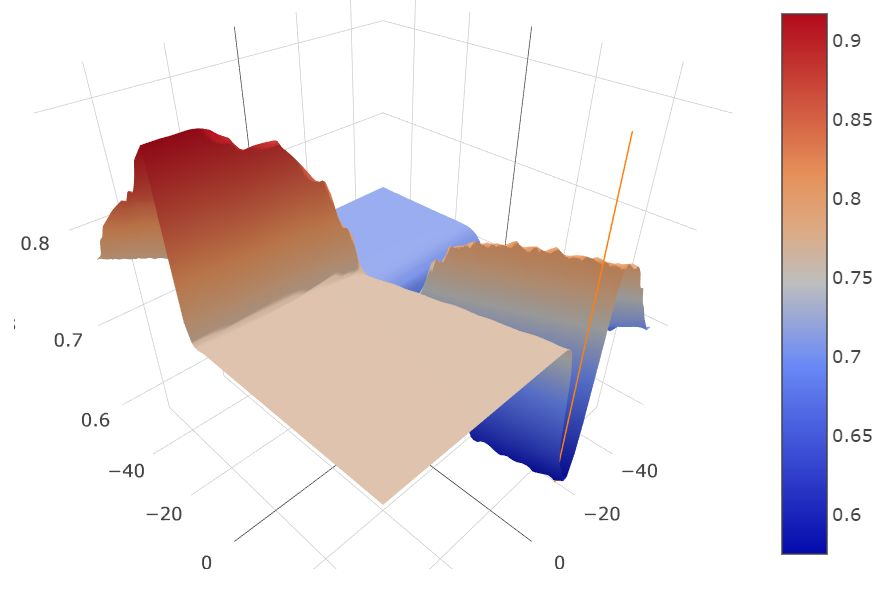
模型的泛化能力仅和Hessian谱有关吗？

我们不妨观察一下示意图中用右侧竖条的橙色表示的最优点，我们会发现沿不同方向损失函数表面的平滑度完全不同。那么我们是否应该在各个方向上施加同样的干扰？也许不是。

我们认为需要沿着「扁平」的方向添加更多的噪声。具体而言，我们建议添加的均匀高斯噪声或截断的高斯噪声，它在每个坐标方向上的水平大致与下面的公式成正比

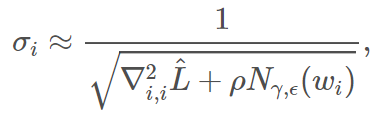
模型的泛化能力仅和Hessian谱有关吗？

其中 ρ 是 Hessian 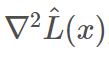模型的泛化能力仅和Hessian谱有关吗？和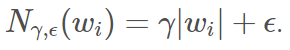的局部 Lipschitz 常数

模型的泛化性能度量

正如 Dinh 等人《Sharp Minima Can Generalize For Deep Nets》和 Neyshabur《Exploring Generalization in Deep Learning》等人讨论的那样，Hessian 谱本身可能并不足以确定模型的泛化能力。特别是对于使用 RELU 作为激励函数的多层感知机模型来说，我们可以重新设置模型的参数并且任意对 Hessian 谱进行放缩而不影响模型的预测性能和泛化能力。

通过使用一些近似方法，我们提出了一种名为「PACGen」的对于模型泛化能力的度量。该度量方法涉及到参数的尺度、Hessian 矩阵，以及通过 Hessian 的 Lipschitz 常数刻画的高阶平滑项。

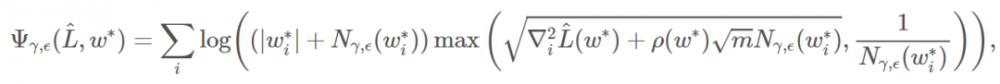
模型的泛化能力仅和Hessian谱有关吗？

其中，我们假设 L_hat(w) 在 w∗ 周围为局部的凸函数。

即使假设我们的度量方法中存在局部的保凸性，在实际应用中，我们可能需要在损失表面的任意点计算该度量。当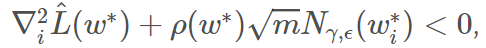模型的泛化能力仅和Hessian谱有关吗？时，我们简单将其视为 0。我们用不同的颜色代表损失函数表面的数值，将度量值绘制如下：

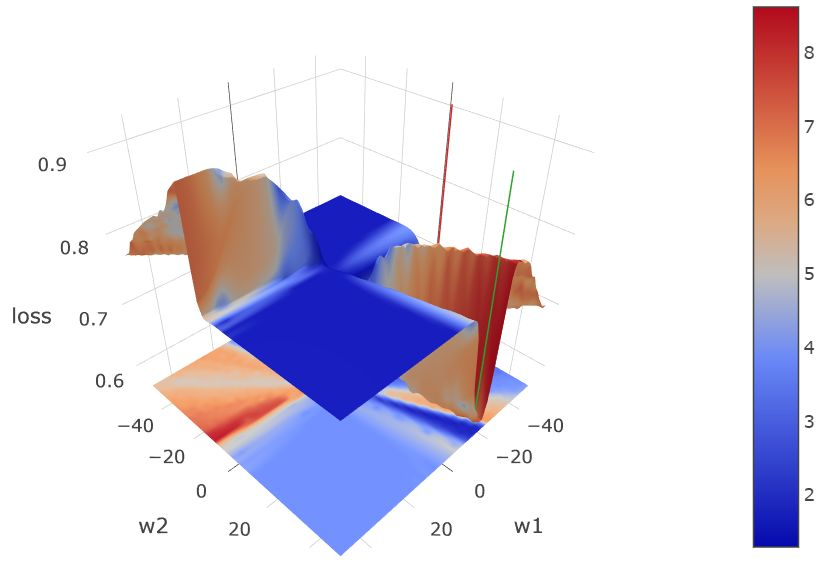
模型的泛化能力仅和Hessian谱有关吗？

共享权值的带有 2 个参数的 5 层多层感知机的示意图。损失函数表面的各种颜色显示了泛化能力的度量值。较低的度量值代表更好的潜在泛化能力。底部平面上的颜色代表了同时考虑损失和泛化能力度量的近似的泛化边界。

如图所示，用绿色竖条表示的该度量方法的全局最优值是很高的。这表明，与红色竖条表示的局部最优值相比，它的泛化能力可能较弱。

另一方面，整体的期望损失由损失和泛化度量一同决定。为此，我们在图的底部绘制了一个彩色平面。投影平面上的颜色标示了一个近似的泛化边界，它同时考虑了损失和泛化能力度量。尽管红色竖条表示局部最优值稍微较高，但是与「尖锐」的全局最优值相比，其整体的泛化边界是相似的。

模型重建

假设该模型生成的是 y=f(x)=p(y|x)，由于我们知道真实的分布为 p(x)，我们可以重建联合分布 p(x,y)=p(x)p(y|x)。举例而言，我们可以首先从 p(x) 中抽样得到 x，然后使用该模型来预测 y_hat=f(x)。下文显示了从真实分布抽样得到的样本，以及在损失函数取「尖锐」的最小值和「平滑」的最小值时得到的分布。

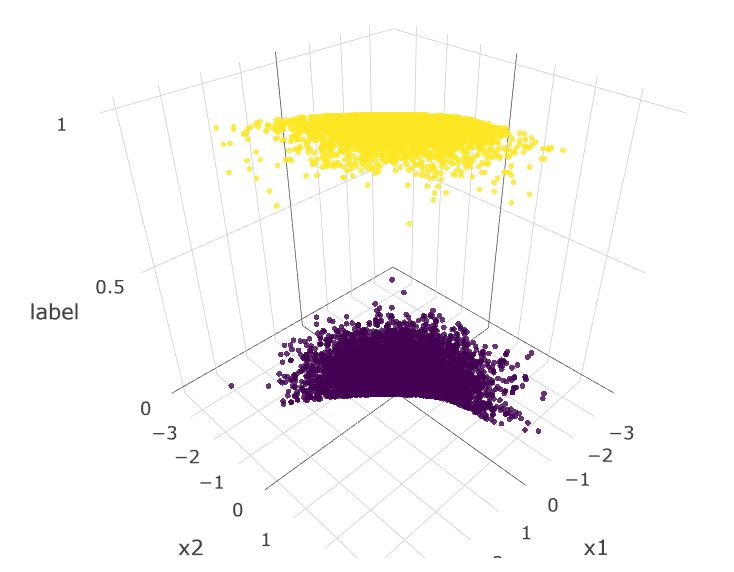
模型的泛化能力仅和Hessian谱有关吗？

从真实分布中抽样得到的样本。

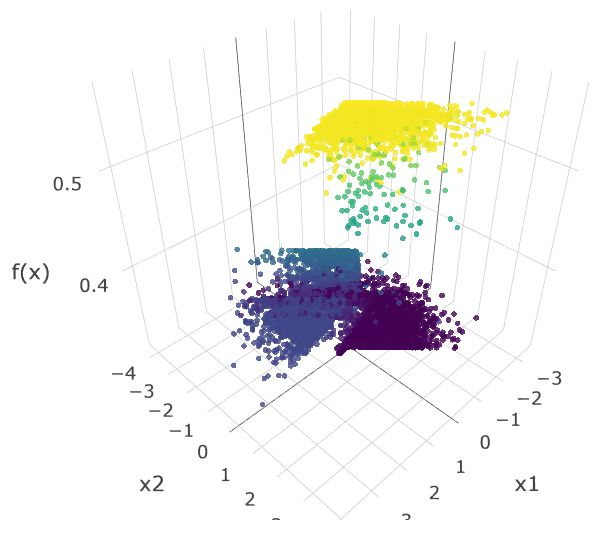
模型的泛化能力仅和Hessian谱有关吗？

在损失函数取「尖锐」的最小值的情况下预测出的标签。

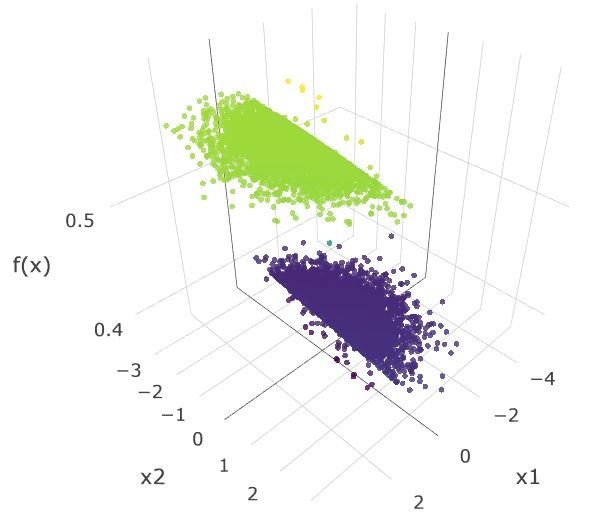
模型的泛化能力仅和Hessian谱有关吗？

在损失函数取「平滑」的最小值时预测出的标签。

尽管「尖锐」的最小值能更好地拟合标签，在「平滑」最小值处取得的预测函数似乎有更简单的决策边界。

在真实数据集上得到的 PACGen

PACGen 度量是在不同的批尺寸和学习率的情况下通过一个 Pytorch 模型计算得到的。我们观察到了和 Keskar 等人相类似的结果：随着批尺寸的增加，测试损失和训练损失之间的差异逐渐增大。我们提出的度量模型的泛化能力仅和Hessian谱有关吗？也显示出了同样的趋势。

项目地址：https://github.com/pytorch/examples/tree/master/mnist

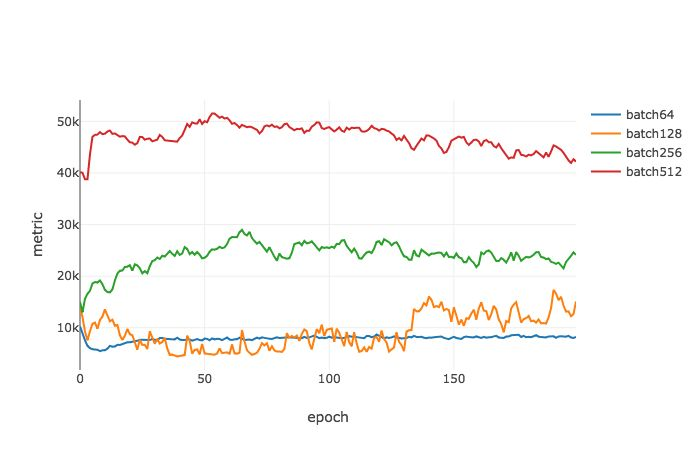
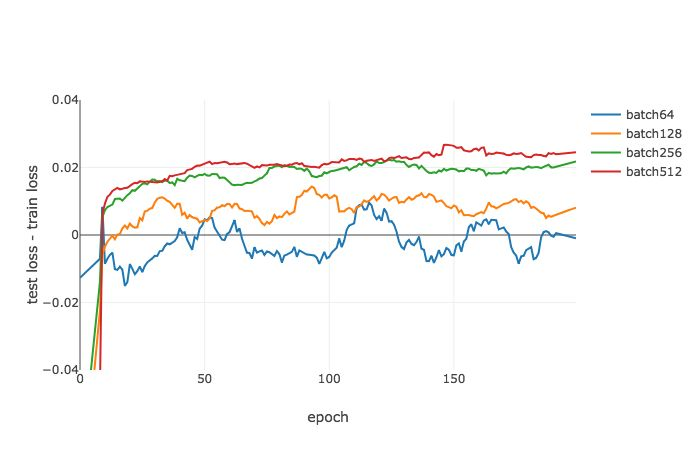
模型的泛化能力仅和Hessian谱有关吗？

测试误差和训练误差对比示意图

泛化能力差距示意图，Ψγ=0.1,ϵ=0.1 时不同批尺寸下在 MNIST 数据集上多轮训练后函数的变化情况。随机梯度下降（SGD）被用作优化器，在所有情况下使用 0.1 作为学习率。随着批处理规模增大，Ψγ,ϵ(^L,w∗) 不断增加。该趋势和损失的真实差距的变化趋势是一致的。

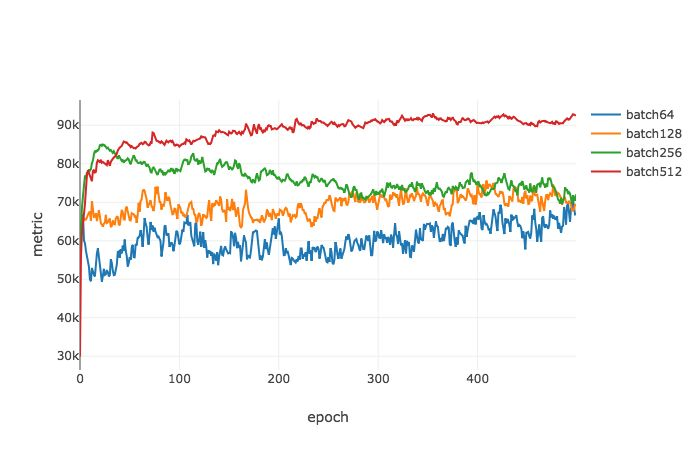
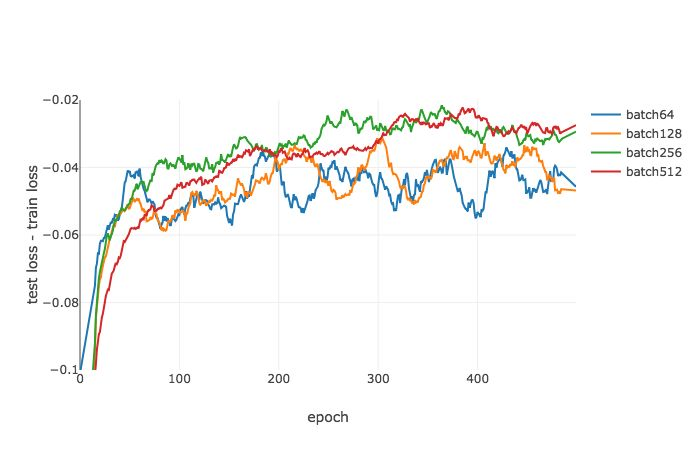
模型的泛化能力仅和Hessian谱有关吗？

测试损失和训练损失对比图

泛化能力差距示意图，Ψγ=0.1,ϵ=0.1 时不同批尺寸下在 CIFAR-10 数据集上多轮训练后函数的变化情况。随机梯度下降（SGD）被用作优化器，在所有情况下使用 0.1 作为学习率。

当我们将批尺寸设置为 256 时，变化情况是相似的。随着学习率减小，测试损失和训练损失之间的差距增大，这与通过 Ψγ,ϵ(^L,w∗) 计算得到的变化趋势是一致的。

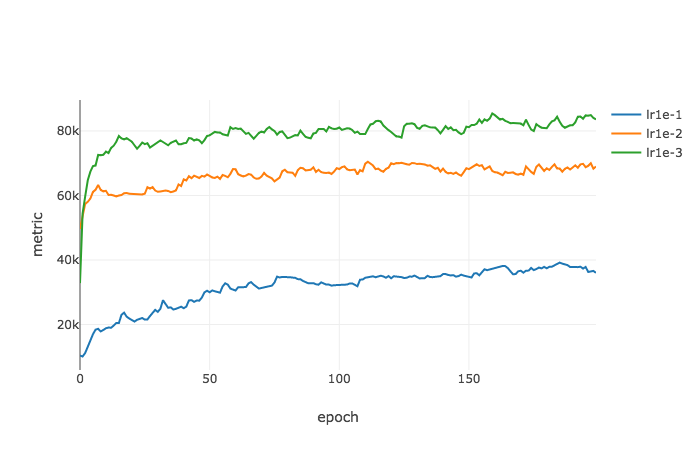
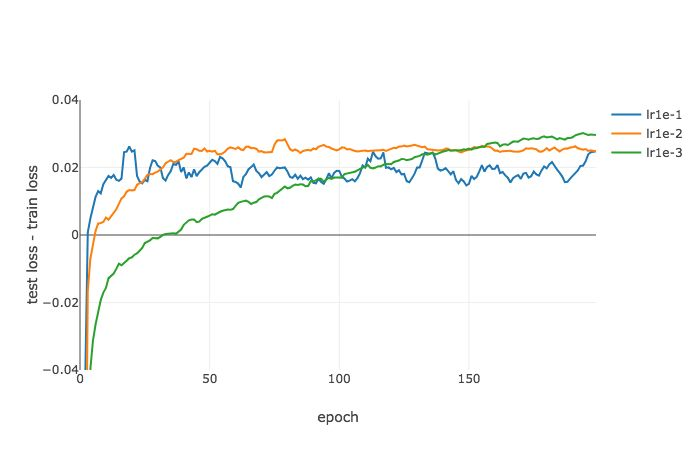
模型的泛化能力仅和Hessian谱有关吗？

测试损失和训练损失对比图

泛化能力差距示意图，Ψγ=0.1,ϵ=0.1 时不同批尺寸下在 MNIST 数据集上多轮训练后函数的变化情况。随机梯度下降（SGD）被用作优化器，在所有情况下批处理规模被设置为 256。随着学习率减小，Ψγ,ϵ(^L,w∗) 不断增大。该趋势与损失的真实差距的变化趋势一致。

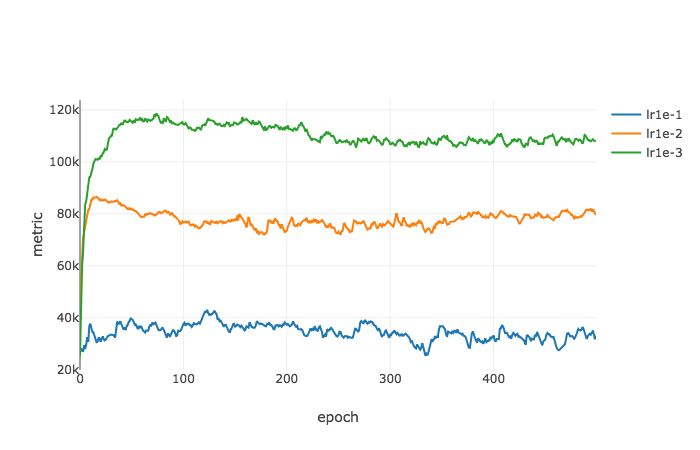
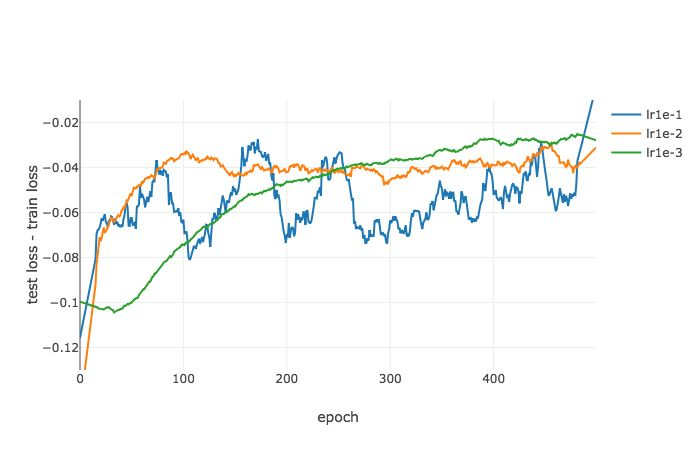
模型的泛化能力仅和Hessian谱有关吗？

测试损失和训练损失对比图

泛化能力差距示意图，Ψγ=0.1,ϵ=0.1 时不同批尺寸下在 CIFAR-10 数据集上多轮训练后函数的变化情况。随机梯度下降（SGD）被用作优化器，在所有情况下批处理规模被设置为 256。

受扰动的优化

PAC-Bayes 边界说明，为了得到更好的泛化能力，我们应该对受扰动的损失进行优化而不是对真实损失进行优化，特别是在每个参数受扰动的程度是根据局部平滑属性设置的情况下。我们观察到，这种对受扰动的模型的优化在 CIFAR-10，CIFAR-100，以及 tiny Imagenet 等数据集上的模型性能得到了提升。

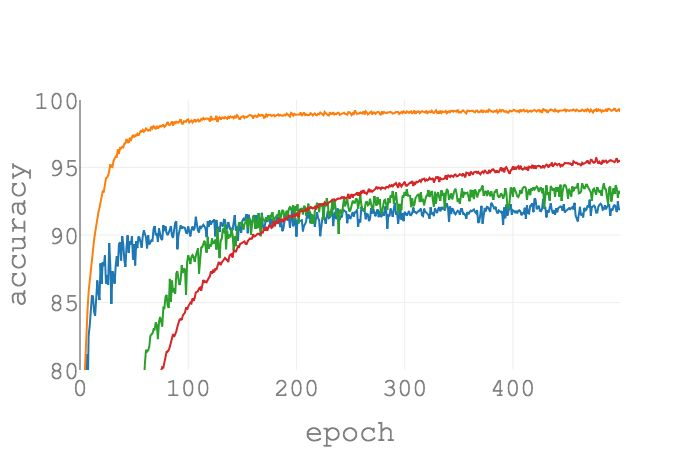
模型的泛化能力仅和Hessian谱有关吗？

在 CIFAR-10 上使用 ADAM 作为优化器的实验结果

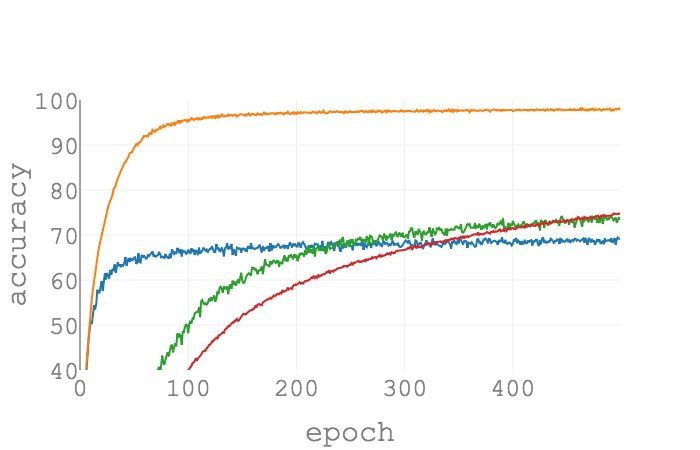
模型的泛化能力仅和Hessian谱有关吗？

在 CIFAR-100 上使用 ADAM 作为优化器的实验结果 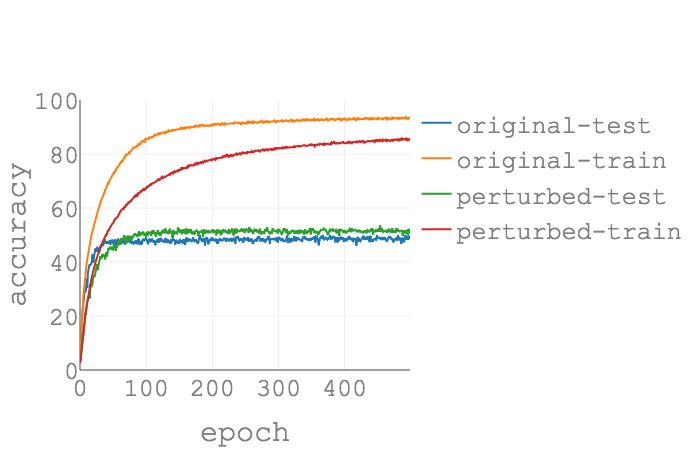模型的泛化能力仅和Hessian谱有关吗？

在 tiny Imagenet 上使用随机梯度下降（SGD）作为优化器的实验结果

结语

我们在 PAC-Bayes 框架下将解的平滑性和模型的泛化能力联系在了一起。我们从理论上证明了模型的泛化能力和 Hessian、解的平滑性、参数的尺度以及训练样本的数量是有关的。我们基于泛化边界提出了一种新的度量方法测试模型的泛化能力，并提出了一种新的扰动算法用来根据 Hessian 调整扰动水平。最后，我们从经验上说明了我们算法和一个正则化器的效果是类似的，都能在未知的数据上获得更好的泛化性能。要想了解包括关于证明和假设在内的更多细节，请参考我们论文的预印本。