转载

散列表

是根据键 (Key) 而直接访问在内存存储位置的数据结构。也就是说，它通过计算一个关于键值的函数，将所需查询的数据映射到表中一个位置来访问记录，这加快了查找速度。这个映射函数称做散列函数，存放记录的数组称做散列表。

通俗的解释

一个通俗的例子是，为了查找电话簿中某人的号码，可以创建一个按照人名首字母顺序排列的表（即建立人名到首字母的一个函数关系），在首字母为W的表中查找 王 姓的电话号码，显然比直接查找就要快得多。这里使用人名作为关键字， 取首字母 是这个例子中散列函数的函数法则，存放首字母的表对应散列表。关键字和函数法则理论上可以任意确定。

基本思想

若关键字为，则其值存放在的存储位置上。由此，不需比较便可直接取得所查记录。称这个对应关系为散列函数

散列表几个重要概念：

散列函数、装载因子、散列冲突

装载因子：

= 填入表中的元素个数 / 散列表的长度

是散列表装满程度的标志因子。由于表长是定值，与“填入表中的元素个数”成正比，所以，越大，表明填入表中的元素越多，产生冲突的可能性就越大；反之，越小，标明填入表中的元素越少，产生冲突的可能性就越小。实际上，散列表的平均查找长度是载荷因子的函数，只是不同处理冲突的方法有不同的函数。

对于开放定址法，荷载因子是特别重要因素，应严格限制在 0.7-0.8 以下。超过 0.8 ，查表时的CPU缓存不命中（ cache missing ）按照指数曲线上升。因此，一些采用开放定址法的 hash 库，如 Java 的系统库限制了荷载因子为 0.75 ，超过此值将 resize 散列表。

散列冲突：

就是指多个元素通过散列函数计算得到的散列地址是相同的。

散列函数：

散列函数选取原则：

好的散列函数 = 计算简单 + 分布均匀

数据结构中的散列函数：

1，直接定址法：取关键字或关键字的某个线性函数值为散列地址。即或，其中为常数。

2，数字分析法：数字分析法通常适合处理散列表中可能出现的关键字都是事先知道的，例如我们现在要存储某家公司员工登记表，如果用手机号作为关键字，那么我们发现抽取后面的四位数字作为散列地址是不错的选择，同理存储身份证号码时，也可以采用这样的逻辑。

3，平方去中法：平方取中法是将关键字平方之后取中间若干位数字作为散列地址。这种方法适用于不知道关键字的分布，且数值的位数又不是很大的情况。

3，随机数法：选择一个随机数，取关键字的随机函数值为它的散列地址，

4，除留取余法：取关键字被某个不大于散列表表长 m 的数 p 除后所得的余数为散列地址。即 p 为小于m的最大质数，所谓素数就是指只能被 1 与它本身整除的数。

主要的散列冲突的解决办法

开放寻址法：

所谓的开放定址法就是一旦发生了冲突，就去寻找下一个空的散列地址，只要散列表足够大，空的散列地址总能找到，并将记录存入。

主要是有 线性探查 平方探查

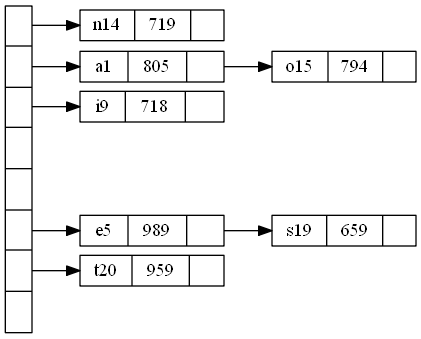
拉链法（链地址法）将散列到同一个存储位置的所有元素保存在一个链表中。

再散列法：

即在上次散列计算发生冲突时，利用该次冲突的散列函数地址产生新的散列函数地址，直到冲突不再发生。

Example

开放定址法

散列表查找的伪代码

// 使用除留余数法
int Hash(int key)
{
    return key % HASHSIZE;        //除数一般小于等于表长的最大素数
}

// 插入关键字到散列表
void InsertHash(HashTable *H, int key)
{
    int addr;

    addr = Hash(key);     //只是得到一个偏移地址

    while( H->elem[addr] != NULLKEY )   // 如果不为空，则冲突出现
    {
        addr = (addr + 1) % HASHSIZE;   // 开放定址法的线性探测
    }

    H->elem[addr] = key;
}

// 散列表查找关键字
int SearchHash(HashTable H, int key, int *addr)
{
    *addr = Hash(key);

    while( H.elem[*addr] != key )
    {
        *addr = (*addr + 1) % HASHSIZE;
        if( H.elem[*addr] == NULLKEY || *addr == Hash(key) )   //后面那个条件说明循环回到原点
        {
            return -1;
        }
    }

    return 0;
}
复制代码

`Java` 中的散列

Java 中的散列冲突解决方法就是上文中提到的开放定址法。散列函数如下。

static final int hash(Object key) { 
        int h;
        return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
    }
复制代码

散列查找方法

public V get(Object key) {
        Node<K,V> e;
        return (e = getNode(hash(key), key)) == null ? null : e.value;
    }
    
    final Node<K,V> getNode(int hash, Object key) {
        Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
        if ((tab = table) != null && (n = tab.length) > 0 &&
            (first = tab[(n - 1) & hash]) != null) {
            if (first.hash == hash && // always check first node
                ((k = first.key) == key || (key != null && key.equals(k))))
                return first;
            if ((e = first.next) != null) {
                if (first instanceof TreeNode)
                    return ((TreeNode<K,V>)first).getTreeNode(hash, key);
                do {
                    if (e.hash == hash &&
                        ((k = e.key) == key || (key != null && key.equals(k))))
                        return e;
                } while ((e = e.next) != null);
            }
        }
        return null;
    }

复制代码

散列表的插入

public V put(K key, V value) {
        return putVal(hash(key), key, value, false, true);
    }
    
    final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
                   boolean evict) {
        Node<K,V>[] tab; Node<K,V> p; int n, i;
        if ((tab = table) == null || (n = tab.length) == 0)
            n = (tab = resize()).length;
        if ((p = tab[i = (n - 1) & hash]) == null)
            tab[i] = newNode(hash, key, value, null);
        else {
            Node<K,V> e; K k;
            if (p.hash == hash &&
                ((k = p.key) == key || (key != null && key.equals(k))))
                e = p;
            else if (p instanceof TreeNode)
                e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
            else {
                for (int binCount = 0; ; ++binCount) {
                    if ((e = p.next) == null) {
                        p.next = newNode(hash, key, value, null);
                        if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
                            treeifyBin(tab, hash);
                        break;
                    }
                    if (e.hash == hash &&
                        ((k = e.key) == key || (key != null && key.equals(k))))
                        break;
                    p = e;
                }
            }
            if (e != null) { // existing mapping for key
                V oldValue = e.value;
                if (!onlyIfAbsent || oldValue == null)
                    e.value = value;
                afterNodeAccess(e);
                return oldValue;
            }
        }
        ++modCount;
        if (++size > threshold)
            resize();
        afterNodeInsertion(evict);
        return null;
    }
复制代码

原文 https://juejin.im/post/5bf7a293e51d45599d422c0c

正文到此结束