转载

HashMap实现原理

HashMap 是在JDK1.2中引入的一种 K/V对 形式的集合类.
在底层, HashMap 通过 数组和单链表 组合的结构形式来存储数据,数组在这作为一个外部结构,数组中的每个节点被称做 Bucket(桶) ,而 桶是由在单链表构成 , JDK1.8 之后为了解决长链表下,查询和插入效率低下的情况,又引入了红黑树的作为桶的实现方式 ,
桶中的各节点是由 HashMap 定义的 Node 内部类生成的,是普通的链表节点类.

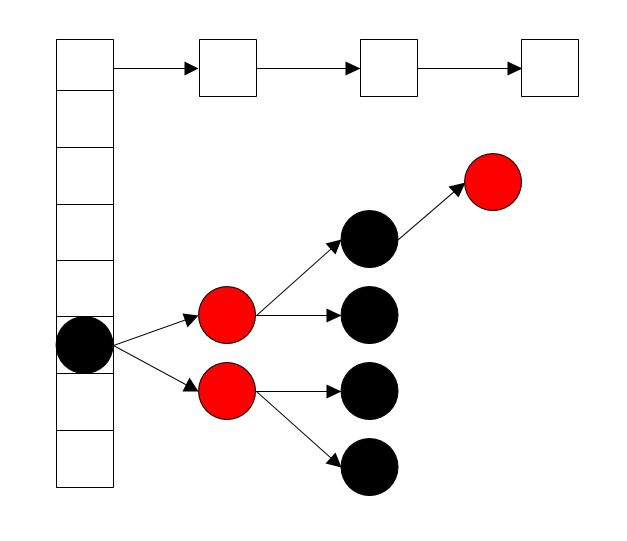
注意: HashMap 是线程不安全的,多线程情况下可能会出现环路(后面会讲) ,多线程状态下还是使用 ConcurrentHashMap 比较合适.

重点参数

HashMap 的参数不多,除去当做默认属性的静态常量和底层数组对象,就只有以下五个

transient Node<K,V>[] table;
transient int size
transient int modCount; 
int threshold;
final float loadFactor;
复制代码

table 就是整个 HashMap 的底层数组, table 的初始化并不在构造函数中完成,而是在 resize() 方法中完成.
- table 的初始化可能有点绕,构造函数中最多指定了阈值 threshold 和负载因子 loadFactor 并没有容量相关,但是在 resize() 方法中会根据旧容量和旧阈值判断新容量是等于默认容量,旧阈值或者两倍旧容量 ,最后根据新容量创建新数组
loadFactor 就是所谓的负载因子,默认为0.75,是控制扩容时机的关键属性,因为扩容发生在当前元素个数超过阈值时,而阈值等于当前容量乘以负载因子.
modCount 为修改计数,是 fast-fail 机制的关键参数.在对 Map 中的元素做新增/删除操作时会自增,但修改不会(putVal()方法中覆盖原值)

新增逻辑

HashMap 的新增过程重点主要还是定位, 如何确定元素在数组中的位置 , HashMap 采用的就是 Hash算法
1. 首先 HashMap 会根据 Key 的hash值,按照表达式 (n - 1) & hash 计算出桶的下标
2. 如果此时桶为空,会创建一个新的 Node ,作为链表的第一个元素,直接存放在数组中.(以前还听说过什么链表首节点为空的情况,是假的.)
3. 如果节点存在又会区分树节点(TreeNode)和普通节点(Node)两种情况.
```
TreeNode
```
另外新增前会判断底层数组 table 是否初始化,新增后会判断该桶大小是否超过的8,超过则转化为红黑树,再判断整个数组是否需要扩容.
Hash 同时也叫散列,可以把任意长度的输入通过算法,换算成固定长度的输出,不同元素通过 Hash 算法获得的下标一致可以被称之为 冲突或者碰撞 , Hash 算法的要求就是使元素尽量少的发生碰撞,从而均匀的散布在 数组中 .而发生碰撞时,像 HashMap 这种以一个列表下挂的方式可以被称为 拉链法 .

查找逻辑

此处的查找逻辑是指调用 get() 方法,通过 key 值查找的情况,如果自己遍历的另说.
1. 同样是根据表达式 (n - 1) & hash 计算出桶的下标(可以说是相当重要了),若得到的桶为空,直接返回null
2. 不为空时则会遍历整个桶,并根据 key.equals(k) 判断是否相等
3. 遍历的方法也会根据节点类型的不同而不同,但是区分节点前直接存放在数组中的头结点是要先进行判断的.感觉上性能影响不大吧
从查找的过程可以看出,确定桶下标的计算不存在随机性,时间复杂度就为O(1),具体的性能体现在遍历这一块,链表查询的时间复杂度为O(n),所以链表越长遍历时间也就越长,插入和查找的效率也就越低.所以在 JDK1.8 之后引入的红黑树作为桶的另一种实现方法.当链表长度大于 8 时,桶的实现会转化为 红黑树 .
HashMap 的性能很大一部分取决于 Hash 算法.

RESIZE逻辑

通过插入和查找我们可以知道,在数组大小不变的情况下,**链表越长或者说树的高度越高性能都会降低,**所以此时很有必要通过扩容数组的方式,重新排列桶中元素,降低链表长度,减少树的高度.
首先,触发扩容的情况是 size > threshold 即元素个数大于阈值.整个扩容过程可以简单的拆分为以下几步:
1. 对数组进行扩充,一般情况下是 数组容量和阈值都变为原来的两倍 .
  - 此间会有上限判断,容量最大为 1 << 30 也就是1的30次方.
2. 遍历旧数组,重新判断元素的位置并散布到新数组.
resize() 方法中重新散布元素的方法还是很有意思的除去单元素链表和红黑树(桶的容量在1~7之间)
- 首先将新数组分为两部分 lo 和 hi (源码是loHead和hiHead,我猜时low和high,怎么这么缩写随意), lo 表示0到旧容量部分, hi 表示余下算是新加入的部分,并以此创建两个链表
- 根据表达式 e.hash & oldCap 判断元素是否分布在 lo 部分,是就挂到 lo 链表下面,否就挂到 hi 链表下面.
- lo 链表挂到和旧数组相同位置的桶,而 hi 则挂到下标为 原下标 + 旧数组容量 的桶.
  - 此处的依据就是 e.hash & (oldCap - 1) + oldCap == e.hash & (oldCap << 1) -1
可以看出 resize() 方法会调整全部的元素散列情况,因此过于频繁的 resize 会降低 HashMap 的性能, 因此如果一开始可以大概知道所需要存放的元素个数时,尽量直接指定容量大小.
JDK1.7 之前的 resize() 方法在并发条件下可能会发生闭环问题,但在 JDK1.8 之后不会在出现,但并不代表 HashMap 可以在并发条件下使用了,小部分情况还是会出现数据丢失等问题.
介绍 JDK1.8 之前的闭环问题详情的文章
- 疫苗：JAVA HASHMAP的死循环