转载

62. Unique Paths

A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).

How many possible unique paths are there?

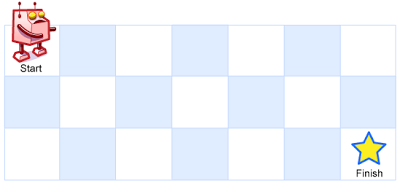
62. Unique Paths

above is a 7 x 3 grid. How many possible unique paths are there?

Note: m and n will be at most 100.

Example 1:

Input: m = 3, n = 2
Output: 3
Explanation:
From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Right -> Down
2. Right -> Down -> Right
3. Down -> Right -> Right

Example 2:

Input: m = 7, n = 3
Output: 28

难度：medium

题目：

在m * n 的格子左上角放置一个机器人，机器人在任何时候只能向右或向下移动，机器人尝试移动到格子的最右下角。有多少种可能的走法？

思路：动态规划，grid[m][n] = grid[m - 1][n] + grid[m][n - 1]

Runtime: 0 ms, faster than 100.00% of Java online submissions for Unique Paths.

Memory Usage: 23.6 MB, less than 41.57% of Java online submissions for Unique Paths.

class Solution {
    public int uniquePaths(int m, int n) {
        int[][] grid = new int[m][n];
        for (int i = 0; i < n; i++) {
            grid[0][i] = 1;
        }
        for (int i = 0; i < m; i++) {
            grid[i][0] = 1;
        }
        
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                grid[i][j] = grid[i - 1][j] + grid[i][j - 1];
            }
        }
        
        return grid[m - 1][n - 1];
    }
}

原文 https://segmentfault.com/a/1190000018121345

正文到此结束