转载

剑指offer解析-下（Java实现）

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点，只能调整树中结点指针的指向。

public TreeNode Convert(TreeNode root) {
}
复制代码

解析

典型的二叉树分解问题，我们可以定义一个黑盒 transform ，它的目的是将二叉树转换成双向链表，那么对于一个当前结点 root ，首先将其前驱结点（BST中前驱结点指中序序列的前一个数值，也就是当前结点的左子树上最右的结点，如果左子树为空则没有前驱结点）和后继结点（当前结点的右子树上的最左结点，如果右子树为空则没有后继结点），然后使用黑盒 transform 将左子树和右子树转换成双向链表，最后将当前结点和左子树形成的链表链起来（通过之前保存的前驱结点）和右子树形成的链表链起来（通过之前保存的后继结点），整棵树的转换完毕。

public TreeNode Convert(TreeNode root) {
    if(root == null){
        return null;
    }

    //head is the most left node
    TreeNode head = root;
    while(head.left != null){
        head = head.left;
    }
    transform(root);
    return head;
}

//transform a tree to a double-link list
public void transform(TreeNode root){
    if(root == null){
        return;
    }
    TreeNode pre = root.left, next = root.right;
    while(pre != null && pre.right != null){
        pre = pre.right;
    }
    while(next != null && next.left != null){
        next = next.left;
    }

    transform(root.left);
    transform(root.right);
    //asume the left and right has transformed and what's remaining is link the root
    root.left = pre;
    if(pre != null){
        pre.right = root;
    }
    root.right = next;
    if(next != null){
        next.left = root;
    }
}
复制代码

字符串全排列

题目描述

输入一个字符串,按字典序打印出该字符串中字符的所有排列。例如输入字符串abc,则打印出由字符a,b,c所能排列出来的所有字符串abc,acb,bac,bca,cab和cba。

解析

定义一个递归体 generate(char[] arr, int index, TreeSet<String> res) ，其中 char[] arr 和 index 组合表示上层状态给当前状态传递的信息，即 arr 中 0 ~ index-1 是已生成好的串，现在你（当前状态）要确定 index 位置上应该放什么字符（你可以从 index ~ arr.length - 1 上任选一个字符），然后将 index + 1 应该放什么字符递归交给子过程处理，当某个状态要确定 arr.length 上应该放什么字符时说明 0 ~ arr.length-1 位置上的字符已经生成好了，因此递归终止，将生成好的字符串记录下来（这里由于要求不能重复且按字典序排列，因此我们可以使用JDK中红黑树的实现 TreeSet 来做容器）

public ArrayList<String> Permutation(String str) {
    ArrayList<String> res = new ArrayList();
    if(str == null || str.length() == 0){
        return res;
    }
    TreeSet<String> set = new TreeSet();
    generate(str.toCharArray(), 0, set);
    res.addAll(set);
    return res;
}

public void generate(char[] arr, int index, TreeSet<String> res){
    if(index == arr.length){
        res.add(new String(arr));
    }
    for(int i = index ; i < arr.length ; i++){
        swap(arr, index, i);
        generate(arr, index + 1, res);
        swap(arr, index, i);
    }
}

public void swap(char[] arr, int i, int j){
    if(arr == null || arr.length == 0 || i < 0 || j > arr.length - 1){
        return;
    }
    char tmp = arr[i];
    arr[i] = arr[j];
    arr[j] = tmp;
}
复制代码

注意：上述代码的第 19 行有个坑，笔者曾因忘记写第19行而排错许久，由于你任选一个 index ~ arr.length - 1 位置上的字符与 index 位置上的交换并将交换生成的结果交给了子过程（第 17,18 行），但你不应该影响后续选取其他字符放到 index 位置上而形成的结果，因此需要再交换回来（第 19 行）

数组中出现次数超过一半的数

题目描述

数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字。例如输入一个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了5次，超过数组长度的一半，因此输出2。如果不存在则输出0。

public int MoreThanHalfNum_Solution(int [] arr) {
}
复制代码

解析

方法一：基于partition查找数组中第k大的数

如果我们将数组排序，最快也要 O(nlogn) ，排序后的中位数自然就是出现次数超过长度一半的数。

我们知道快排的 partition 操作能够将数组按照一个基准划分成小于部分和大于等于部分并返回这个基准在数组中的下标，虽然一次 partition 并不能使数组整体有序，但是能够返回随机选择的数在 partition 之后的下标 index ，这个下标标识了它是第 index 大的数，这也意味着我们要求数组中第 k 大的数不一定要求数组整体有序。

于是我们在首次对整个数组 partition 之后将返回的 index 与 n/2 进行比较，并调整下一次 partition 的范围直到 index = n/2 为止我们就找到了。

这个时间复杂度需要使用 Master 公式计算（计算过程参见 www.zhenganwen.top/62859a9a.ht… 使用 partition 查找数组中第k大的数时间复杂度为 O(n) ，最后不要忘了验证一下 index = n/2 上的数出现的次数是否超过了长度的一半。

public int MoreThanHalfNum_Solution(int [] arr) {
    if(arr == null || arr.length == 0){
        return 0;
    }
    if(arr.length == 1){
        return arr[0];
    }

    int index = partition(arr, 0, arr.length - 1);
    int half = arr.length >> 1;// 0 <= half <= arr.length - 1
    while(index != half){
        index = index > k ? partition(arr, 0, index - 1) : partition(arr, index + 1, arr.length - 1);
    }

    int count = 0;
    for(int i = 0 ; i < arr.length ; i++){
        count = (arr[i] == arr[index]) ? ++count : count;
    }

    return (count > arr.length / 2) ? arr[index] : 0;
}

public int partition(int[] arr, int start, int end){
    if(arr == null || arr.length == 0 || start < 0 || end > arr.length - 1 || start > end){
        throw new IllegalArgumentException();
    }
    if(start == end){
        return end;
    }
    int random = start + (int)(Math.random() * (end - start + 1));
    swap(arr, random, end);
    int small = start - 1;
    for(int i = start ; i < end ; i++){
        if(arr[i] < arr[end]){
            swap(arr, ++small, i);
        }
    }

    swap(arr, ++small, end);

    return small;
}

public void swap(int[] arr, int i, int j){
    int t = arr[i];
    arr[i] = arr[j];
    arr[j] = t;
}
复制代码

方法二

使用一个 target 记录一个数，并使用 count 记录它出现的次数
初始时 target = arr[0] ， count = 1 ，表示 arr[0] 出现了1次
从第二个元素开始遍历数组，如果遇到的数不等于 target 就将 count 减1，否则加1
如果遍历到某个数时， count 为0了，那么就将 target 设置为该数，并将 count 置1，继续向后遍历

如果存在出现次数超过一半的数，那么必定是 target 最后一次被设置时的数。

public int MoreThanHalfNum_Solution(int [] arr) {
    if(arr == null || arr.length == 0){
        return 0;
    }
    //此题需要抓住出现次数超过数组长度的一半这个点来想
    //使用一个计数器，如果这个数出现一次就自增，否则自减，如果自减为0则更新被记录的数
    //如果存在出现次数大于一半的数，那么最后一次被记录的数就是所求之数
    int target = arr[0], count = 1;
    for(int i = 1 ; i < arr.length ; i++){
        if(count == 0){
            target = arr[i];
            count = 1;
        }else{
            count = (arr[i] == target) ? ++count : --count;
        }
    }

    if(count == 0){
        return 0;
    }

    //不要忘了验证！！！
    count = 0;
    for(int i = 0 ; i < arr.length ; i++){
        count = (arr[i] == target) ? ++count : count;
    }

    return (count > arr.length / 2) ? target : 0;
}
复制代码

最小的k个数

题目描述

输入n个整数，找出其中最小的K个数。例如输入4,5,1,6,2,7,3,8这8个数字，则最小的4个数字是1,2,3,4,。

public ArrayList<Integer> GetLeastNumbers_Solution(int [] arr, int k) {
    
}
复制代码

解析

与上一题的求数组第k大的数如出一辙，如果某次 partition 之后你得到了第k大的数的下标，那么根据 partitin 规则该下标左边的数均比该下标上的数小，最小的k个数自然就是此时的 0~k-1 下标上的数

public ArrayList<Integer> GetLeastNumbers_Solution(int [] arr, int k) {
    ArrayList<Integer> res = new ArrayList<Integer>();
    if(arr == null || arr.length == 0 || k <= 0 || k > arr.length){
        //throw new IllegalArgumentException();
        return res;
    }

    int index = partition(arr, 0, arr.length - 1);
    k = k - 1;
    while(index != k){
        index = index > k ? partition(arr, 0, index - 1) : partition(arr, index + 1, arr.length - 1);
    }

    for(int i = 0 ; i <= k ; i++){
        res.add(arr[i]);
    }

    return res;
}

public int partition(int[] arr, int start, int end){
    if(arr == null || arr.length == 0 || start < 0 || end > arr.length - 1 || start > end){
        throw new IllegalArgumentException();
    }
    if(start == end){
        return end;
    }

    int random = start + (int)(Math.random() * (end - start + 1));
    swap(arr, random, end);
    int small = start - 1;
    for(int i = start ; i < end ; i++){
        if(arr[i] < arr[end]){
            swap(arr, ++small, i);
        }
    }

    swap(arr, ++small, end);
    return small;
}

public void swap(int[] arr, int i, int j){
    int t = arr[i];
    arr[i] = arr[j];
    arr[j] = t;
}
复制代码

连续子数组的最大和

题目描述

HZ偶尔会拿些专业问题来忽悠那些非计算机专业的同学。今天测试组开完会后,他又发话了:在古老的一维模式识别中,常常需要计算连续子向量的最大和,当向量全为正数的时候,问题很好解决。但是,如果向量中包含负数,是否应该包含某个负数,并期望旁边的正数会弥补它呢？例如:{6,-3,-2,7,-15,1,2,2},连续子向量的最大和为8(从第0个开始,到第3个为止)。给一个数组，返回它的最大连续子序列的和，你会不会被他忽悠住？(子向量的长度至少是1)

public int FindGreatestSumOfSubArray(int[] arr) {
    
}
复制代码

解析

暴力解

暴力法是找出所有子数组，然后遍历求和，时间复杂度为 O(n^3)

public int FindGreatestSumOfSubArray(int[] arr) {
    if(arr == null || arr.length == 0){
        return 0;
    }
    int max = Integer.MIN_VALUE;

    //start
    for(int i = 0 ; i < arr.length ; i++){
        //end
        for(int j = i ; j < arr.length ; j++){
            //sum
            int sum = 0;
            for(int k = i ; k <= j ; k++){
                sum += arr[k];
            }
            max = Math.max(max, sum);
        }
    }

    return max;
}
复制代码

最优解

使用一个 sum 记录累加和，初始时为0，遍历数组：

如果遍历到 i 时，发现 sum 小于0，那么丢弃这个累加和，将 sum 重置为 0
将当前元素累加到 sum 上，并更新最大和 maxSum

public int FindGreatestSumOfSubArray(int[] arr) {
    if(arr == null || arr.length == 0){
        return 0;
    }
    int sum = 0, max = Integer.MIN_VALUE;
    for(int i = 0 ; i < arr.length ; i++){
        if(sum < 0){
            sum = 0;
        }
        sum += arr[i];
        max = Math.max(max, sum);
    }

    return max;
}
复制代码

整数中1出现的次数（从1到n整数中1出现的次数）

题目描述

求出1~13的整数中1出现的次数,并算出100~1300的整数中1出现的次数？为此他特别数了一下1~13中包含1的数字有1、10、11、12、13因此共出现6次,但是对于后面问题他就没辙了。ACMer希望你们帮帮他,并把问题更加普遍化,可以很快的求出任意非负整数区间中1出现的次数（从1 到 n 中1出现的次数）。

解析

遍历一遍不就完了吗

当然，你可从1遍历到n，然后将当前被遍历的到的数中1出现的次数累加到结果中可以很容易地写出如下代码：

public int NumberOf1Between1AndN_Solution(int n) {
    if(n < 1){
        return 0;
    }
    int res = 0;
    for(int i = 1 ; i <= n ; i++){
        res += count(i);
    }
    return res;
}

public int count(int n){
    int count = 0;
    while(n != 0){
        //取个位
        count = (n % 10 == 1) ? ++count : count;
        //去掉个位
        n /= 10;
    }
    return count;
}
复制代码

但n多大就会循环多少次，这并不是面试官所期待的，这时我们就需要找规律看是否有捷径可走

不用数我也知道

以 51234 这个数为例，我们可以先将 51234 划分成 1~1234 （去掉最高位）和 1235~51234 两部分来求解。下面先分析 1235~51234 这个区间的结果：

所有的数中，1在最高位（万位）出现的次数

对于 1235~51234 ，最高位为1时（即万位为1时）的数有 10000~19999 这10000个数，也就是说1在最高位（万位）出现的次数为10000，因此我们可以得出结论：如果最高位大于1，那么在最高位上1出现的次数为最高位对应的单位（本例中为一万次）；但如果最高位为1，比如 1235~11234 ，那么次数就为去掉最高位之后的数了， 11234 去掉最高位后是 1234 ，即1在最高位上出现的次数为 1234
所有的数中，1在非最高位上出现的次数

我们可以进一步将 1235~51234 按照最高位的单位划分成4个区间（能划分成几个区间由最高位上的数决定，这里最高位为5，所以能划分5个大小为一万子区间）：
```
1235~11234
11235~21234
21235~31234
31235~41234
41235~51234
```
而每个数不考虑万位（因为1在万位出现的总次数在步骤1中已统计好了），其余四位（个、十、百、千）取一位放1（比如千位），剩下的3位从 0~9 中任意选（ 10 * 10 * 10 ），那么仅统计1在千位上出现的次数之和就是： 5(子区间数) * 10 * 10 * 10 ，还有百位、十位、个位，结果为： 4 * 10 * 10 * 10 * 5 。

因此非高位上1出现的总次数的计算通式为： (n-1) * 10^(n-2) * 十进制最高位上的数 （其中 n 为十进制的总位数）

于是 1235 ~ 51234 之间所有的数的所有的位上1出现的次数的综合我们就计算出来了

剩下 1 ~ 1234 ，你会发现这与 1 ~ 51234 的问题是一样的，因此可以做递归处理，即子过程也会将 1 ~ 1234 也分成 1 ~ 234 和 235 ~ 1234 两部分，并计算 235~1234 而将 1~234 又进行递归处理。

而递归的终止条件如下：

如果 1~n 中的 n ： 1 <= n <= 9 ，那么就可以直接返回1了，因为只有数1出现了一次1
如果 n == 0 ，比如将 10000 划分成的两部分是 0 ~ 0(10000去掉最高位后的结果) 和 1 ~ 10000 ，那么就返回0

public int NumberOf1Between1AndN_Solution(int n) {
    if(n < 1){
        return 0;
    }
    return process(n);
}

public int process(int n){
    if(n == 0){
        return 0;
    }
    if(n < 10 && n > 0){
        return 1;
    }
    int res = 0;
    //得到十进制位数
    int bitCount = bitCount(n);
    //十进制最高位上的数
    int highestBit = numOfBit(n, bitCount);
    //1、统计最高位为1时，共有多少个数
    if(highestBit > 1){
        res += powerOf10(bitCount - 1);
    }else{
        //highestBit == 1
        res += n - powerOf10(bitCount - 1) + 1;
    }
    //2、统计其它位为1的情况
    res += powerOf10(bitCount - 2) * (bitCount - 1) * highestBit;
    //3、剩下的部分交给递归
    res += process(n % powerOf10(bitCount - 1));
    return res;
}

//返回10的n次方
public int powerOf10(int n){
    if(n == 0){
        return 1;
    }
    boolean minus = false;
    if(n < 0){
        n = -n;
        minus = true;
    }
    int res = 1;
    for(int i = 1 ; i <= n ; i++){
        res *= 10;
    }
    return minus ? 1 / res : res;
}

public int bitCount(int n){
    int count = 1;
    while((n /= 10) != 0){
        count++;
    }
    return count;
}

public int numOfBit(int n, int bit){
    while(bit-- > 1){
        n /= 10;
    }
    return n % 10;
}
复制代码

笔者曾纠结，对于一个四位数，每个位上出现1时都统计了一遍会不会有重复，比如 11111 这个数在最高位为1时的 10000 ~ 19999 统计了一遍，在统计非最高位的其他位上为1时又统计了4次，总共被统计了5次，而这个数1出现的次数也确实是5次，因此没有重复。

把数组排成最小的数

题目描述

输入一个正整数数组，把数组里所有数字拼接起来排成一个数，打印能拼接出的所有数字中最小的一个。例如输入数组{3，32，321}，则打印出这三个数字能排成的最小数字为321323。

解析

这是一个贪心问题，你发现将数组按递增排序之后依次连接起来的结果并不是最优的结果，于是需要寻求贪心策略，对于这类最小数和最小字典序的问题而言，贪心策略是：如果 3 和 32 相连的结果大于 32 和 3 相连的结果，那么视作 3 比 32 大，最后我们需要按照按照这种策略将数组进行升序排序，以得到首尾相连之后的结果是最小数字（最小字典序）。

public String PrintMinNumber(int [] numbers) {
    if(numbers == null || numbers.length == 0){
        return "";
    }
    List<Integer> list = new ArrayList();
    for(int num : numbers){
        list.add(num);
    }
    Collections.sort(list, new MyComparator());
    StringBuilder res = new StringBuilder("");
    for(Integer integer : list){
        res.append(integer.toString());
    }
    return res.toString();
}

class MyComparator implements Comparator<Integer>{
    public int compare(Integer i1, Integer i2){
        String s1 = i1.toString() + i2.toString();
        String s2 = i2.toString() + i1.toString();
        return Integer.parseInt(s1) - Integer.parseInt(s2);
    }
}
复制代码

丑数

题目描述

把只包含质因子2、3和5的数称作丑数（Ugly Number）。例如6、8都是丑数，但14不是，因为它包含质因子7。习惯上我们把1当做是第一个丑数。求按从小到大的顺序的第N个丑数。

解析

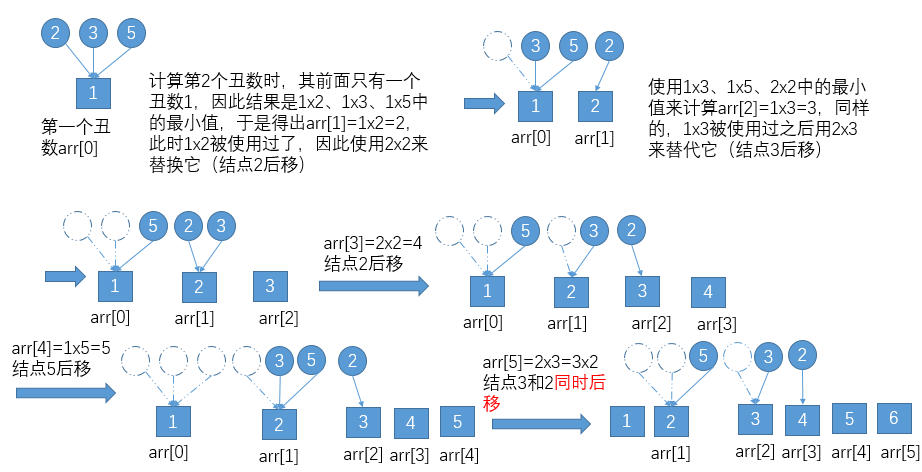
老实说，在《剑指offer》上看这道题的时候每太看懂，以至于第一遍在牛客网OJ这道题的时候都是背下来写上去的，直到这第二遍总结时才弄清整个思路，思路的核心就是第一个丑数是1（题目给的），此后的每一个丑数都是由之前的某个丑数与2或3或5的乘积得来

public int GetUglyNumber_Solution(int index) {
    if(index < 1){
        //throw new IllegalArgumentException("index must bigger than one");
        return 0;
    }
    if(index == 1){
        return 1;
    }

    int[] arr = new int[index];
    arr[0] = 1;
    int indexOf2 = 0, indexOf3 = 0, indexOf5 = 0;
    for(int i = 1 ; i < index ; i++){
        arr[i] = Math.min(arr[indexOf2] * 2, Math.min(arr[indexOf3] * 3, arr[indexOf5] * 5));
        indexOf2 = (arr[indexOf2] * 2 <= arr[i]) ? ++indexOf2 : indexOf2;
        indexOf3 = (arr[indexOf3] * 3 <= arr[i]) ? ++indexOf3 : indexOf3;
        indexOf5 = (arr[indexOf5] * 5 <= arr[i]) ? ++indexOf5 : indexOf5;
    }

    return arr[index - 1];
}
复制代码

第一个只出现一次的字符

题目描述

在一个字符串(0<=字符串长度<=10000， 全部由字母组成 )中找到第一个只出现一次的字符,并返回它的位置, 如果没有则返回 -1（需要区分大小写）.

解析

可以从头遍历字符串，并使用一个表记录每个字符第一次出现的位置（初始时表中记录的位置均为-1），如果记录当前被遍历字符出现的位置时发现之前已经记录过了（通过查表，该字符的位置不是-1而是大于等于0的一个有效索引），那么当前字符不在答案的考虑范围内，通过将表中该字符的出现索引标记为 -2 来标识。

遍历一遍字符串并更新表之后，再遍历一遍字符串，如果发现某个字符在表中对应的记录是一个有效索引（大于等于0），那么该字符就是整个串中第一个只出现一次的字符。

由于题目标注字符串全都由字母组成，而字母可以使用 ASCII 码表示且 ASCII 范围为 0~255 ，因此使用了一个长度为 256 的数组来实现这张表。用字母的 ASCII 值做索引，索引对应的值就是字母在字符串中第一次出现的位置（初始时为-1，第一次遇到时设置为出现的位置，重复遇到时置为-2）。

public int FirstNotRepeatingChar(String str) {
    if(str == null || str.length() == 0){
        return -1;
    }
    //全部由字母组成
    int[] arr = new int[256];
    for(int i = 0 ; i < arr.length ; i++){
        arr[i] = -1;
    }
    for(int i = 0 ; i < str.length() ; i++){
        int ascii = (int)str.charAt(i);
        if(arr[ascii] == -1){
            //set index of first apearance
            arr[ascii] = i;
        }else if(arr[ascii] >= 0){
            //repeated apearance, don't care
            arr[ascii] = -2;
        }
        //arr[ascii] == -2 -> do not care
    }

    for(int i = 0 ; i < str.length() ; i++){
        int ascii = (int)str.charAt(i);
        if(arr[ascii] >= 0){
            return arr[ascii];
        }
    }

    return -1;
}
复制代码

数组中的逆序对

题目描述

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。即输出P%1000000007

public int InversePairs(int [] arr) {
    if(arr == null || arr.length <= 1){
        return 0;
    }
    return mergeSort(arr, 0, arr.length - 1).pairs;
}
复制代码

输入描述

题目保证输入的数组中没有相同的数字
数据范围：对于%50的数据,size<=10^4；对于%75的数据,size<=10^5；对于%100的数据,size<=2*10^5

解析

借助归并排序的流程，将归并流程中前一个数组的数比后一个数组的数小的情况记录下来。

归并的原始逻辑是根据输入的无序数组返回一个新建的排好序的数组：

public int[] mergeSort(int[] arr, int start, int end){
    if(arr == null || arr.length == 0 || start < 0 || end > arr.length - 1 || start > end){
        throw new IllegalArgumentException();
    }
    if(start == end){
        return new int[]{ arr[end] };
    }

    int[] arr1 = mergeSort(arr, start, mid);
    int[] arr2 = Info right = mergeSort(arr, mid + 1, end);
    int[] copy = new int[arr1.length + arr2.length];
    int p1 = 0, p2 = 0, p = 0;

    while(p1 < arr1.length && p2 < arr2.length){
        if(arr1[p1] > arr2[p2]){
            copy[p++] = arr1[p1++];
        }else{
            copy[p++] = arr2[p2++];
        }
    }
    while(p1 < arr1.length){
        copy[p++] = arr1[p1++];
    }
    while(p2 < arr2.length){
        copy[p++] = arr2[p2++];
    }
    return copy;
}
复制代码

而我们需要再此基础上对子状态收集的信息进行改造，假设左右两半部分分别有序了，那么进行 merge 的时候，不应是从前往后复制了，这样当 arr1[p1] > arr2[p2] 的时候并不知道 arr2 的 p2 后面还有多少元素是比 arr1[p1] 小的，要想一次比较就统计出 arr2 中所有比 arr1[p1] 小的数需要将 p1,p2 从 arr1,arr2 的尾往前遍历：

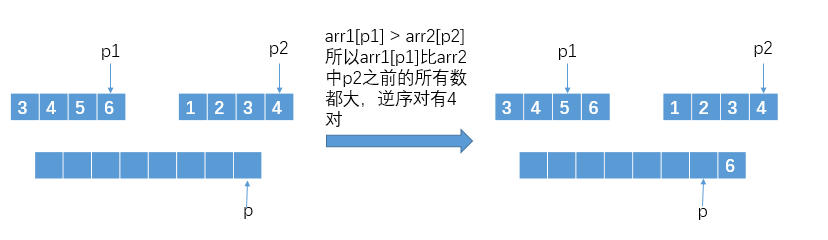
而将比较后较大的数移入辅助数组的逻辑还是一样。这样当前递归状态需要收集左半子数组和右半子数组的变成有序过程中记录的逆序对数和自己 merge 记录的逆序对数之和就是当前状态要返回的信息，并且 merge 后形成的有序辅助数组也要返回。

public int InversePairs(int [] arr) {
    if(arr == null || arr.length <= 1){
        return 0;
    }
    return mergeSort(arr, 0, arr.length - 1).pairs;
}

class Info{
    int arr[];
    int pairs;
    Info(int[] arr, int pairs){
        this.arr = arr;
        this.pairs = pairs;
    }
}

public Info mergeSort(int[] arr, int start, int end){
    if(arr == null || arr.length == 0 || start < 0 || end > arr.length - 1 || start > end){
        throw new IllegalArgumentException();
    }
    if(start == end){
        return new Info(new int[]{arr[end]}, 0);
    }

    int pairs = 0;
    int mid = start + ((end - start) >> 1);
    Info left = mergeSort(arr, start, mid);
    Info right = mergeSort(arr, mid + 1, end);
    pairs += (left.pairs + right.pairs) % 1000000007;

    int[] arr1 = left.arr, arr2 = right.arr, copy = new int[arr1.length + arr2.length];
    int p1 = arr1.length - 1, p2 = arr2.length - 1, p = copy.length - 1;

    while(p1 >= 0 && p2 >= 0){
        if(arr1[p1] > arr2[p2]){
            pairs += (p2 + 1);
            pairs %= 1000000007;
            copy[p--] = arr1[p1--];
        }else{
            copy[p--] = arr2[p2--];
        }
    }

    while(p1 >= 0){
        copy[p--] = arr1[p1--];
    }
    while(p2 >= 0){
        copy[p--] = arr2[p2--];
    }

    return new Info(copy, pairs % 1000000007);
}
复制代码

两个链表的第一个公共结点

题目描述

输入两个链表，找出它们的第一个公共结点。

public ListNode FindFirstCommonNode(ListNode pHead1, ListNode pHead2) {

}
复制代码

解析

首先我们要分析两个链表的组合状态，根据有环、无环相互组合只可能会出现如下几种情况：

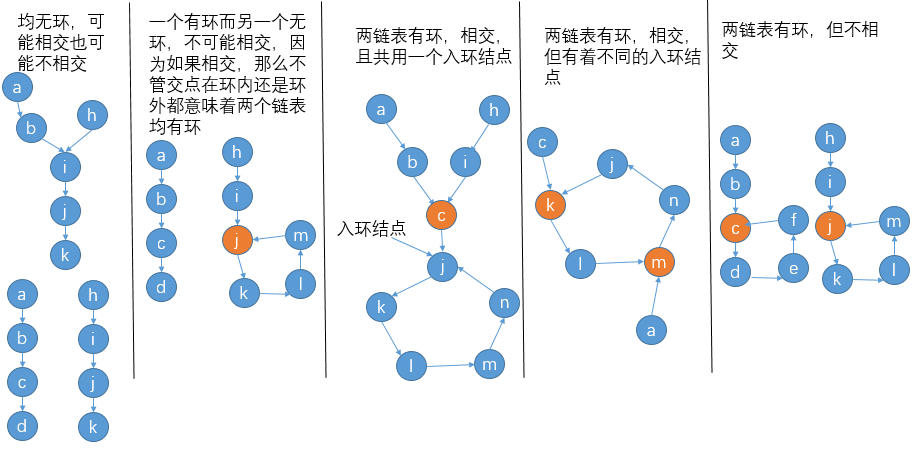
于是我们首先要判断两个链表是否有环，判断链表是否有环以及有环链表的入环结点在哪已有前人给我们总结好了经验：

使用一个快指针和一个慢指针同时从首节点出发，快指针一次走两步而慢指针一次走一步，如果两指针相遇则说明有环，否则无环
如果两指针相遇，先将快指针重新指向首节点，然后两指针均一次走一步，再次相遇时的结点就是入环结点

public ListNode FindFirstCommonNode(ListNode pHead1, ListNode pHead2) {
    //若其中一个链表为空则不存在相交问题
    if(pHead1 == null || pHead2 == null){
        return null;
    }
    ListNode ringNode1 = ringNode(pHead1);
    ListNode ringNode2 = ringNode(pHead2);
    //如果一个有环，另一个无环
    if((ringNode1 == null && ringNode2 != null) ||
       (ringNode1 != null && ringNode2 == null)){
        return null;
    }
    //如果两者都无环，判断是否共用尾结点
    else if(ringNode1 == null && ringNode2 == null){
        return firstCommonNode(pHead1, pHead2, null);
    }
    //剩下的情况就是两者都有环了
    else{
        //如果入环结点相同，那么第一个相交的结点肯定在入环结点之前
        if(ringNode1 == ringNode2){
            return firstCommonNode(pHead1, pHead2, ringNode1);
        }
        //如果入环结点不同，看能否通过ringNode1的后继找到ringNode2
        else{
            ListNode p = ringNode1;
            while(p.next != ringNode1){
                p = p.next;
                if(p == ringNode2){
                    break;
                }
            }
            //如果能找到，那么第一个相交的结点既可以是ringNode1也可以是ringNode2
            return (p == ringNode2) ? ringNode1 : null;
        }
    }
}

//查找两链表的第一个公共结点，如果两链表无环，则传入common=null，如果都有环且入环结点相同，那么传入common=入环结点
public ListNode firstCommonNode(ListNode pHead1, ListNode pHead2, ListNode common){
    ListNode p1 = pHead1, p2 = pHead2;
    int len1 = 1, len2 = 1, gap = 0;
    while(p1.next != common){
        p1 = p1.next;
        len1++;
    }
    while(p2.next != common){
        p2 = p2.next;
        len2++;
    }
    //如果是两个无环链表，要判断一下是否有公共尾结点
    if(common == null && p1 != p2){
        return null;
    }
    gap = len1 > len2 ? len1 - len2 : len2 - len1;
    //p1指向长链表，p2指向短链表
    p1 = len1 > len2 ? pHead1 : pHead2;
    p2 = len1 > len2 ? pHead2 : pHead1;
    while(gap-- > 0){
        p1 = p1.next;
    }
    while(p1 != p2){
        p1 = p1.next;
        p2 = p2.next;
    }
    return p1;
}

//判断链表是否有环，没有返回null，有则返回入环结点（整个链表是一个环时入环结点就是头结点）
public ListNode ringNode(ListNode head){
    if(head == null){
        return null;
    }
    ListNode p1 = head, p2 = head;
    while(p1.next != null && p1.next.next != null){
        p1 = p1.next.next;
        p2 = p2.next;
        if(p1 == p2){
            break;
        }
    }

    if(p1.next == null || p1.next.next == null){
        return null;
    }

    p1 = head;
    while(p1 != p2){
        p1 = p1.next;
        p2 = p2.next;
    }
    //可能整个链表就是一个环，这时入环结点就是头结点！！！
    return p1 == p2 ? p1 : head;
}
复制代码

数字在排序数组中出现的次数

题目描述

统计一个数字在排序数组中出现的次数。

public int GetNumberOfK(int [] array , int k) {

}
复制代码

解析

我们可以分两步解决，先找出数值为k的连续序列的左边界，再找右边界。可以采用二分的方式，以查找左边界为例：如果 arr[mid] 小于 k 那么移动左指针，否则移动右指针（初始时左指针指向 -1 ，而右指针指向尾元素 arr.length ），当两个指针相邻时，左指针及其左边的数均小于 k 而右指针及其右边的数均大于或等于 k ，因此此时右指针就是要查找的左边界，同样的方式可以求得右边界。

值得注意的是，笔者曾将左指针初始化为 0 而右指针初始化为 arr.length - 1 ，这与指针指向的含义是相悖的，因为左指针指向的元素必须是小于 k 的，而我们并不能保证 arr[0] 一定小于 k ，同样的我们也不能保证 arr[arr.length - 1] 一定大于等于 k 。

还有一点就是如果数组中没有 k 这个算法是否依然会返回一个正确的值（0），这也是需要验证的。

public int GetNumberOfK(int [] arr , int k) {
    if(arr == null || arr.length == 0){
        return 0;
    }
    if(arr.length == 1){
        return (arr[0] == k) ? 1 : 0;
    }

    int start, end, left, right;
    for(start = -1, end = arr.length ; end > start && end - start != 1 ;){
        int mid = start + ((end - start) >> 1);
        if(arr[mid] >= k){
            end = mid;
        }else{
            start = mid;
        }
    }
    left = end;
    for(start = -1, end = arr.length; end > start && end - start != 1 ;){
        int mid = start + ((end - start) >> 1);
        if(arr[mid] > k){
            end = mid;
        }else{
            start = mid;
        }
    }
    right = start;
    return right - left + 1;
}
复制代码

二叉树的深度

题目描述

输入一棵二叉树，求该树的深度。从根结点到叶结点依次经过的结点（含根、叶结点）形成树的一条路径，最长路径的长度为树的深度。

public int TreeDepth(TreeNode root) {
}
复制代码

解析

TreeDepth
base case

public class Solution {
    public int TreeDepth(TreeNode root) {
        if(root == null){
            return 0;
        }
        return Math.max(TreeDepth(root.left), TreeDepth(root.right)) + 1;
    }
}
复制代码

平衡二叉树

题目描述

输入一棵二叉树，判断该二叉树是否是平衡二叉树。

public boolean IsBalanced_Solution(TreeNode root) {

}
复制代码

解析

判断当前这棵树是否是平衡二叉所需要收集的信息：

左子树、右子树各自是平衡二叉树吗（需要收集子树是否是平衡二叉树）
如果1成立，还需要收集左子树和右子树的高度，如果高度相差不超过1那么当前这棵树才是平衡二叉树（需要收集子树的高度）

class Info{
    boolean isBalanced;
    int height;
    Info(boolean isBalanced, int height){
        this.isBalanced = isBalanced;
        this.height = height;
    }
}
复制代码

递归体的定义：（这里高度之差不超过1中的 left.height - right.height == 0 容易被忽略）

public boolean IsBalanced_Solution(TreeNode root) {
    return process(root).isBalanced;
}

public Info process(TreeNode root){
    if(root == null){
        return new Info(true, 0);
    }
    Info left = process(root.left);
    Info right = process(root.right);
    if(!left.isBalanced || !right.isBalanced){
        //如果左子树或右子树不是平衡二叉树，那么当前这棵树肯定也不是，树高度信息也就没用了
        return new Info(false, 0);
    }
    //高度之差不超过1
    if(left.height - right.height == 1 || left.height - right.height == -1 ||
       left.height - right.height == 0){
        return new Info(true, Math.max(left.height, right.height) + 1);
    }
    return new Info(false, 0);
}
复制代码

数组中只出现一次的数字

题目描述

一个整型数组里除了两个数字之外，其他的数字都出现了偶数次。请写程序找出这两个只出现一次的数字。

解析

如果没有解过类似的题目，思路比较难打开。面试官可能会提醒你，如果是让你求一个整型数组里只有一个数只出现了一次而其它数出现了偶数次呢？你应该联想到：

偶数次相同的数异或的结果是0
任何数与0异或的结果是它本身

于是将数组从头到尾求异或和便可得知结果。那么对于此题，能否将数组分成这样的两部分呢：每个部分只有一个数出现了一次，其他的数都出现偶数次。

如果我们仍将整个数组从头到尾求异或和，那结果应该和这两个只出现一次的数的异或结果相同，目前我们所能依仗的也就是这个结果了，能否靠这个结果将数组分成想要的两部分？

由于两个只出现一次的数（用A和B表示）异或结果 A ^ B 肯定不为0，那么 A ^ B 的二进制表示中肯定包含数值为1的bit位，而这个位上的1肯定是由A或B提供的，也就是说我们能根据 这个bit位上的数是否为1 来区分A和B，那剩下的数呢？

由于剩下的数都出现偶数次，因此相同的数都会被分到一边（按照某个bit位上是否为1来分）。

public void FindNumsAppearOnce(int [] arr,int num1[] , int num2[]) {
    if(arr == null || arr.length <= 1){
        return;
    }
    int xorSum = 0;
    for(int num : arr){
        xorSum ^= num;
    }
    //取xorSum二进制表示中低位为1的bit位，将其它的bit位 置0
    //比如：xorSum = 1100，那么 (1100 ^ 1011) & 1100 = 0100，只剩下一个为1的bit位
    xorSum = (xorSum ^ (xorSum - 1)) & xorSum;

    for(int num : arr){
        num1[0] = (num & xorSum) == 0 ? num1[0] ^ num : num1[0];
        num2[0] = (num & xorSum) != 0 ? num2[0] ^ num : num2[0];
    }
}
复制代码

和为S的连续正数序列

题目描述

小明很喜欢数学,有一天他在做数学作业时,要求计算出9~16的和,他马上就写出了正确答案是100。但是他并不满足于此,他在想究竟有多少种连续的正数序列的和为100(至少包括两个数)。没多久,他就得到另一组连续正数和为100的序列:18,19,20,21,22。现在把问题交给你,你能不能也很快的找出所有和为S的连续正数序列? Good Luck!

public ArrayList<ArrayList<Integer> > FindContinuousSequence(int sum) {

}
复制代码

输出描述

输出所有和为S的连续正数序列。序列内按照从小至大的顺序，序列间按照开始数字从小到大的顺序

解析

将 1 ~ (S / 2 + 1) 区间的数 n 依次加入到队列中（因为从 S/2 + 1 之后的任意两个正数之和都大于 S ）：

将 n 加入到队列 queue 中并将队列元素之和 queueSum 更新，更新 queueSum 之后如果发现等于 sum ，那么将此时的队列快照加入到返回结果 res 中，并弹出队首元素（ 保证下次入队操作时队列元素之和是小于sum的 ）
更新 queueSum 之后如果发现大于 sum ，那么循环弹出队首元素直到 queueSum <= Sum ，如果循环弹出之后发现 queueSum == sum 那么将队列快照加入到 res 中，并弹出队首元素（ 保证下次入队操作时队列元素之和是小于sum的 ）；如果 queueSum < sum 那么入队下一个 n

于是有如下代码：

public ArrayList<ArrayList<Integer>> FindContinuousSequence(int sum) {
    ArrayList<ArrayList<Integer>> res = new ArrayList();
    if(sum <= 1){
        return res;
    }
    LinkedList<Integer> queue = new LinkedList();
    int n = 1, halfSum = (sum >> 1) + 1, queueSum = 0;
    while(n <= halfSum){
        queue.addLast(n);
        queueSum += n;
        if(queueSum == sum){
            ArrayList<Integer> one = new ArrayList();
            one.addAll(queue);
            res.add(one);
            queueSum -= queue.pollFirst();
        }else if(queueSum > sum){
            while(queueSum > sum){
                queueSum -= queue.pollFirst();
            }
            if(queueSum == sum){
                ArrayList<Integer> one = new ArrayList();
                one.addAll(queue);
                res.add(one);
                queueSum -= queue.pollFirst();
            }
        }
        n++;
    }

    return res;
}
复制代码

我们发现 11~15 和 20~24 行的代码是重复的，于是可以稍微优化一下：

public ArrayList<ArrayList<Integer>> FindContinuousSequence(int sum) {
    ArrayList<ArrayList<Integer>> res = new ArrayList();
    if(sum <= 1){
        return res;
    }
    LinkedList<Integer> queue = new LinkedList();
    int n = 1, halfSum = (sum >> 1) + 1, queueSum = 0;
    while(n <= halfSum){
        queue.addLast(n);
        queueSum += n;
        if(queueSum > sum){
            while(queueSum > sum){
                queueSum -= queue.pollFirst();
            }
        }
        if(queueSum == sum){
            ArrayList<Integer> one = new ArrayList();
            one.addAll(queue);
            res.add(one);
            queueSum -= queue.pollFirst();
        }
        n++;
    }

    return res;
}
复制代码

和为S的两个数字

题目描述

输入一个递增排序的数组和一个数字S，在数组中查找两个数，使得他们的和正好是S，如果有多对数字的和等于S，输出两个数的乘积最小的。

public ArrayList<Integer> FindNumbersWithSum(int [] arr,int sum) {
    
}
复制代码

输出描述

对应每个测试案例，输出查找到的两个数，如果有多对，输出乘积最小的两个。

解析

使用指针 l,r ，初始时 l 指向首元素， r 指向尾元素，当两指针元素之和不等于 sum 且 r 指针在 l 指针右侧时循环：

如果两指针元素之和大于 sum ，那么将 r 指针左移，试图减小两指针之和
如果两指针元素之和小于 sum ，那么将 l 右移，试图增大两指针之和
如果两指针元素之和等于 sum 那么就可以返回了，或者 r 跑到了 l 的左边表名没有和 sum 的两个数，也可以返回了。

public ArrayList<Integer> FindNumbersWithSum(int [] arr,int sum) {
    ArrayList<Integer> res = new ArrayList<Integer>();
    if(arr == null || arr.length <= 1 ){
        return res;
    }
    int l = 0, r = arr.length - 1;
    while(arr[l] + arr[r] != sum && r > l){
        if(arr[l] + arr[r] > sum){
            r--;
        }else{
            l++;
        }
    }
    if(arr[l] + arr[r] == sum){
        res.add(arr[l]);
        res.add(arr[r]);
    }
    return res;
}
复制代码

旋转字符串

题目描述

汇编语言中有一种移位指令叫做循环左移（ROL），现在有个简单的任务，就是用字符串模拟这个指令的运算结果。对于一个给定的字符序列S，请你把其循环左移K位后的序列输出。例如，字符序列S=”abcXYZdef”,要求输出循环左移3位后的结果，即“XYZdefabc”。是不是很简单？OK，搞定它！

public String LeftRotateString(String str,int n) {
    
}
复制代码

解析

将开头的一段子串移到串尾：将开头的子串翻转一下、将剩余的子串翻转一下，最后将整个子串翻转一下。按理来说应该输入 char[] str 的，这样的话这种算法不会使用额外空间。

public String LeftRotateString(String str,int n) {
    if(str == null || str.length() == 0 || n <= 0){
        return str;
    }
    char[] arr = str.toCharArray();
    reverse(arr, 0, n - 1);
    reverse(arr, n, arr.length - 1);
    reverse(arr, 0, arr.length - 1);
    return new String(arr);
}

public void reverse(char[] str, int start, int end){
    if(str == null || str.length == 0 || start < 0 || end > str.length - 1 || start >= end){
        return;
    }
    for(int i = start, j = end ; j > i ; i++, j--){
        char tmp = str[i];
        str[i] = str[j];
        str[j] = tmp;
    }
}
复制代码

翻转单词顺序列

题目描述

牛客最近来了一个新员工Fish，每天早晨总是会拿着一本英文杂志，写些句子在本子上。同事Cat对Fish写的内容颇感兴趣，有一天他向Fish借来翻看，但却读不懂它的意思。例如，“student. a am I”。后来才意识到，这家伙原来把句子单词的顺序翻转了，正确的句子应该是“I am a student.”。Cat对一一的翻转这些单词顺序可不在行，你能帮助他么？

public String LeftRotateString(String str,int n) {
    
}
复制代码

解析

先将整个字符串翻转，最后按照标点符号或空格一次将句中的单词翻转。注意：由于最后一个单词后面没有空格，因此需要单独处理！！！

public String ReverseSentence(String str) {
    if(str == null || str.length() <= 1){
        return str;
    }
    char[] arr = str.toCharArray();
    reverse(arr, 0, arr.length - 1);
    int start = -1;
    for(int i = 0 ; i < arr.length ; i++){
        if(arr[i] != ' '){
            //初始化start
            start = (start == -1) ? i : start;
        }else{
            //如果是空格，不用担心start>i-1，reverse会忽略它
            reverse(arr, start, i - 1);
            start = i + 1;
        }
    }
    //最后一个单词，这里比较容易忽略！！！
    reverse(arr, start, arr.length - 1);

    return new String(arr);
}

public void reverse(char[] str, int start, int end){
    if(str == null || str.length == 0 || start < 0 || end > str.length - 1 || start >= end){
        return ;
    }
    for(int i = start, j = end ; j > i ; i++, j--){
        char tmp = str[i];
        str[i] = str[j];
        str[j] = tmp;
    }
}
复制代码

扑克牌顺子

题目描述

LL今天心情特别好,因为他去买了一副扑克牌,发现里面居然有2个大王,2个小王(一副牌原本是54张^_^)...他随机从中抽出了5张牌,想测测自己的手气,看看能不能抽到顺子,如果抽到的话,他决定去买体育彩票,嘿嘿！！“红心A,黑桃3,小王,大王,方片5”,“Oh My God!”不是顺子.....LL不高兴了,他想了想,决定大/小王可以看成任何数字,并且A看作1,J为11,Q为12,K为13。上面的5张牌就可以变成“1,2,3,4,5”(大小王分别看作2和4),“So Lucky!”。LL决定去买体育彩票啦。现在,要求你使用这幅牌模拟上面的过程,然后告诉我们LL的运气如何，如果牌能组成顺子就输出true，否则就输出false。为了方便起见,你可以认为大小王是0。

解析

先将数组排序（5个元素排序时间复杂O(1）），然后遍历数组统计王的数量和相邻非王牌之间的缺口数（需要用几个王来填）。还有一点值得注意：如果发现两种相同的非王牌，则不可能组成五张不同的顺子。

public boolean isContinuous(int [] arr) {
    if(arr == null || arr.length != 5){
        return false;
    }
    //5 numbers -> O(1)
    Arrays.sort(arr);
    int zeroCount = 0, slots = 0;
    for(int i = 0 ; i < arr.length ; i++){
        //如果遇到两张相同的非王牌则不可能组成顺子，这点很容易忽略！！！
        if(i > 0 && arr[i - 1] != 0){
            if(arr[i] == arr[i - 1]){
                return false;
            }else{
                slots += arr[i] - arr[i - 1] - 1;
            }

        }
        zeroCount = (arr[i] == 0) ? ++zeroCount : zeroCount;
    }

    return zeroCount >= slots;
}
复制代码

孩子们的游戏（圆圈中剩下的数）

题目描述

每年六一儿童节,牛客都会准备一些小礼物去看望孤儿院的小朋友,今年亦是如此。HF作为牛客的资深元老,自然也准备了一些小游戏。其中,有个游戏是这样的:首先,让小朋友们围成一个大圈。然后,他随机指定一个数m,让编号为0的小朋友开始报数。每次喊到m-1的那个小朋友要出列唱首歌,然后可以在礼品箱中任意的挑选礼物,并且不再回到圈中,从他的下一个小朋友开始,继续0...m-1报数....这样下去....直到剩下最后一个小朋友,可以不用表演,并且拿到牛客名贵的“名侦探柯南”典藏版(名额有限哦!!^_^)。请你试着想下,哪个小朋友会得到这份礼品呢？(注：小朋友的编号是从0到n-1)

解析

报数时，在报到 m-1 之前，可通过报数求得报数的结点编号：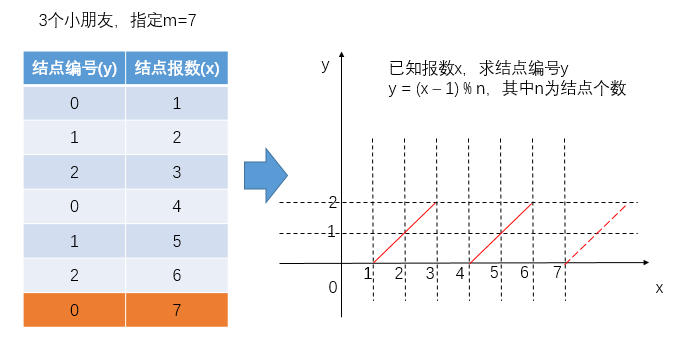
在某个结点（小朋友）出列后的重新编号过程中，可通过新编号求结点的就编号

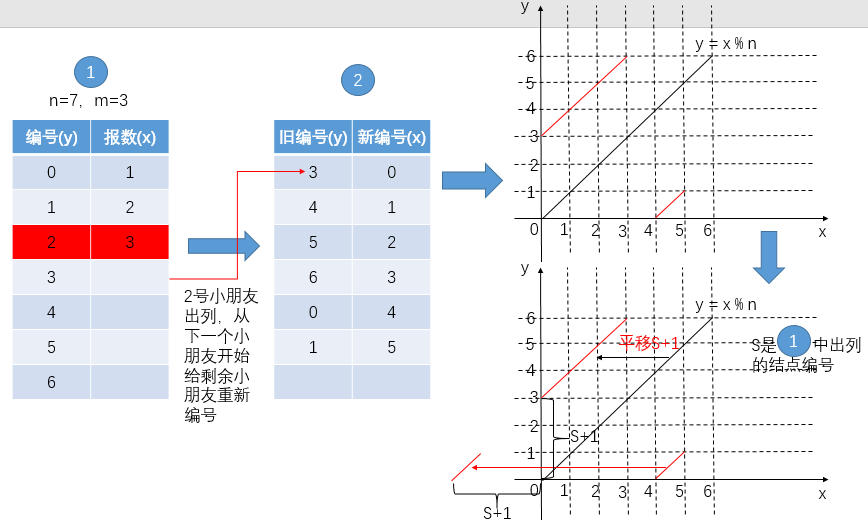
因此在某轮重新编号时，我们能在已知新编号 x 的情况下通过公式 y = (x + S + 1) % n 求得结点重新标号之前的旧编号，上述两步分析的公式整理如下：
1. 某一轮报数出列前： 编号 = （报数 - 1）% 出列前结点个数
2. 某一轮报数出列后： 旧编号 = （新编号 + 出列编号 + 1）% 出列前结点个数 ，因为出列结点是因为报数 m 才出列的，所以有： 出列编号 = （m - 1）% 出列前结点个数
3. 由2可推出： 旧编号 = （新编号 + （m - 1）% 出列前结点个数 + 1）% 出列前结点个数 ，若用 n 表示 出列后 结点个数： y = (x + (m - 1) % n + 1) % n = (x + m - 1) % n + 1

经过上面3步的复杂分析之后，我们得出这么一个通式： 旧编号 = （新编号 + m - 1 ）% 出列前结点个数 + 1 ，于是我们就可以自下而上（用链表模拟出列过程是自上而下），求出**最后一轮重新编号为 1 **的小朋友（只剩他一个了）在倒数第二轮重新编号时的旧编号，自下而上可倒推出这个小朋友在第一轮编号时（这时还没有任何一个小朋友出列过）的原始编号，即目标答案。

注意：式子 y = (x + m - 1) % n + 1 的计算结果不可能为 0 ，因此我们可以按小朋友从 1 开始编号，将最后的计算结果应题目的要求（小朋友从0开始编号）减一个1即可。

public int LastRemaining_Solution(int n, int m) {
    if(n <= 0){
        //throw new IllegalArgumentException();
        return -1;
    }
    //最后一次重新编号：最后一个结点编号为1，出列前结点数为2
    return orginalNumber(2, 0, n, m);
}

//根据出列后的重新编号（newNumber）推导出列前的旧编号（返回值）
//n：出列前有多少小朋友，N：总共有多少个小朋友
public int orginalNumber(int n, int newNumber, int N, int m){
    int lastNumber = (newNumber + m - 1) % n + 1;
    if(n == N){
        return lastNumber;
    }
    return orginalNumber(n + 1, lastNumber, N, m);
}
复制代码

求1+2+3+…+n

题目描述

求1+2+3+...+n，要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句（A?B:C）。

public int Sum_Solution(int n) {
    
}
复制代码

解析

递归轻松解决

既然不允许遍历求和，不如将计算分解，如果知道了 f(n - 1) ， f(n) 则可以通过 f(n - 1) + n 算出：

public int Sum_Solution(int n) {
    if(n == 1){
        return 1;
    }
    return n + Sum_Solution(n - 1);
}
复制代码

不用加减乘除做加法

题目描述

写一个函数，求两个整数之和，要求在函数体内不得使用+、-、*、/四则运算符号。

解析

不要忘了加减乘除是人类熟悉的运算方法，而计算机只知道位运算哦！

我们可以将两数的二进制表示写出来，然后按位与得出进位信息、按位或得出非进位信息，如果进位信息不为0，则循环计算直到进位信息为0，此时异或信息就是两数之和：

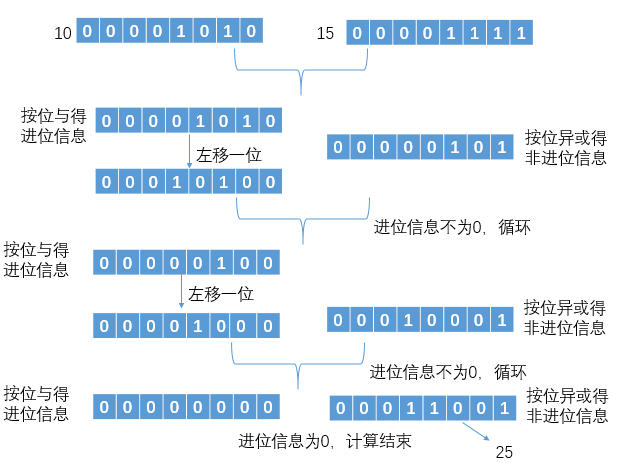
public int Add(int num1,int num2) {
    if(num1 == 0 || num2 == 0){
        return num1 == 0 ? num2 : num1;
    }
    int and = 0, xor = 0;
    do{
        and = num1 & num2;
        xor = num1 ^ num2;
        num1 = and << 1;
        num2 = xor;
    }while(and != 0);

    return xor;
}
复制代码

把字符串转换成整数

题目描述

将一个字符串转换成一个整数(实现Integer.valueOf(string)的功能，但是string不符合数字要求时返回0)，要求不能使用字符串转换整数的库函数。数值为0或者字符串不是一个合法的数值则返回0。

public int StrToInt(String str) {
    
}
复制代码

输入描述

输入一个字符串,包括数字字母符号,可以为空

输出描述

如果是合法的数值表达则返回该数字，否则返回0

示例

输入： +2147483647 ，输出： 2147483647 输入： 1a33 ，输出 0

解析

只有第一个位置上的字符可以是 + 或 - 或数字，其他位置上的字符必须是数字
如果第一个字符是 - ，返回结果必须是负数
如果字符串只有一个字符，且为 + 或 - ，这情况很容易被忽略
在对字符串解析转换时，如果发现溢出（包括正数向负数溢出，负数向正数溢出），必须有所处理（此时可以和面试官交涉），但不能视而不见

public int StrToInt(String str) {
    if(str == null || str.length() == 0){
        return 0;
    }
    boolean minus = false;
    int index = 0;
    if(str.charAt(0) == '-'){
        minus = true;
        index = 1;
    }else if(str.charAt(0) == '+'){
        index = 1;
    }
    //如果只有一个正负号
    if(index == str.length()){
        return 0;
    }

    if(checkInteger(str, index, str.length() - 1)){
        return transform(str, index, str.length() - 1, minus);
    }

    return 0;
}

public boolean checkInteger(String str, int start, int end){
    if(str == null || str.length() == 0 || start < 0 || end > str.length() - 1 || start > end){
        return false;
    }
    for(int i = start ; i <= end ; i++){
        if(str.charAt(i) < '0' || str.charAt(i) > '9'){
            return false;
        }
    }
    return true;
}

public int transform(String str, int start, int end, boolean minus){
    if(str == null || str.length() == 0 || start < 0 || end > str.length() - 1 || start > end){
        throw new IllegalArgumentException();
    }
    int res = 0;
    for(int i = start ; i <= end ; i++){
        int num = str.charAt(i) - '0';
        res = minus ? (res * 10 - num) : (res * 10 + num);
        if((minus && res > 0) || (!minus && res < 0)){
            throw new ArithmeticException("the str is overflow int");
        }
    }
    return res;
}
复制代码

数组中重复的数字

题目描述

在一个长度为n的数组里的所有数字都在0到n-1的范围内。数组中某些数字是重复的，但不知道有几个数字是重复的。也不知道每个数字重复几次。请找出数组中任意一个重复的数字。例如，如果输入长度为7的数组{2,3,1,0,2,5,3}，那么对应的输出是第一个重复的数字2。

// Parameters:
//    numbers:     an array of integers
//    length:      the length of array numbers
//    duplication: (Output) the duplicated number in the array number,length of duplication array is 1,so using duplication[0] = ? in implementation;
//                  Here duplication like pointor in C/C++, duplication[0] equal *duplication in C/C++
//    这里要特别注意~返回任意重复的一个，赋值duplication[0]
// Return value:       true if the input is valid, and there are some duplications in the array number
//                     otherwise false
public boolean duplicate(int numbers[],int length,int [] duplication) {
	
}
复制代码

解析

认真审题发现输入数据是有特征的，即数组长度为 n ，数组中的元素都在 0~n-1 范围内，如果数组中没有重复的元素，那么排序后每个元素和其索引值相同，这就意味着数组中如果有重复的元素，那么数组排序后肯定有元素和它对应的索引是不等的。

顺着这个思路，我们可以将每个元素放到与它相等的索引上，如果某次放之前发现对应的索引上已有了和索引相同的元素，那么说明这个元素是重复的，由于每个元素最多会被调整两次，因此时间复杂 O(n)

public boolean duplicate(int arr[],int length,int [] duplication) {
    if(arr == null || arr.length == 0){
        return false;
    }
    int index = 0;
    while(index < arr.length){
        if(arr[index] == arr[arr[index]]){
            if(index != arr[index]){
                duplication[0] = arr[index];
                return true;
            }else{
                index++;
            }
        }else{
            int tmp = arr[index];
            arr[index] = arr[tmp];
            arr[tmp] = tmp;
        }
    }

    return false;
}
复制代码

构建乘积数组

题目描述

给定一个数组A[0,1,...,n-1],请构建一个数组B[0,1,...,n-1],其中B中的元素B[i]=A[0] A[1] ...*A[i-1] A[i+1] ...*A[n-1]。不能使用除法。

public int[] multiply(int[] arr) {
    
}
复制代码

分析

规律题：

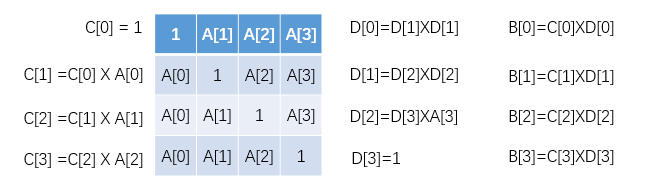
public int[] multiply(int[] arr) {
    if(arr == null || arr.length == 0){
        return arr;
    }
    int len = arr.length;
    int[] arr1 = new int[len], arr2 = new int[len];
    arr1[0] = 1;
    arr2[len - 1] = 1;
    for(int i = 1 ; i < len ; i++){
        arr1[i] = arr1[i - 1] * arr[i - 1];
        arr2[len - 1 - i] = arr2[len - i] * arr[len - i];
    }
    int[] res = new int[len];
    for(int i = 0 ; i < len ; i++){
        res[i] = arr1[i] * arr2[i];
    }

    return res;
}
复制代码

正则表达式匹配

题目描述

请实现一个函数用来匹配包括'.'和' '的正则表达式。模式中的字符'.'表示任意一个字符，而' '表示它前面的字符可以出现任意次（包含0次）。在本题中，匹配是指字符串的所有字符匹配整个模式。例如，字符串"aaa"与模式"a.a"和"ab ac a"匹配，但是与"aa.a"和"ab*a"均不匹配

public boolean match(char[] str, char[] pattern){
    
}
复制代码

解析

使用 p1 指向 str 中下一个要匹配的字符，使用 p2 指向 pattern 中剩下的模式串的首字符

如果 p2 >= pattern.length ，表示模式串消耗完了，这时如果 p1 仍有字符要匹配那么返回 false 否则返回 true
如果 p1 >= str.length ，表示要匹配的字符都匹配完了，但模式串还没消耗完，这时剩下的模式串必须符合 a*b*c* 这样的范式以能够作为空串处理，否则返回 false
p1 和 p2 都未越界，按照 p2 后面是否是 * 来讨论
1. p2 后面如果是 * ，又可按照 pattern[p2] 是否能够匹配 str[p1] 分析：
  1. pattern[p2] == ‘.’ || pattern[p2] == str[p1] ，这时可以选择匹配一个 str[p1] 并继续向后匹配（不用跳过 p2 和其后面的 * ），也可以选择将 pattern[p2] 和其后面的 * 作为匹配空串处理，这时要跳过 p2 和其后面的 *
  2. pattern[p2] != str[p1] ，只能作为匹配空串处理，跳过 p2
2. p2 后面如果不是 * ：
  1. pattern[p2] == str[p1] || pattern[p2] == ‘.’ ， p1,p2 同时后移一个继续匹配
  2. pattern[p2] == str[p1] ，直接返回 false

public boolean match(char[] str, char[] pattern){
    if(str == null || pattern == null){
        return false;
    }
    if(str.length == 0 && pattern.length == 0){
        return true;
    }
    return matchCore(str, 0, pattern, 0);
}

public boolean matchCore(char[] str, int p1, char[] pattern, int p2){
    //模式串用完了
    if(p2 >= pattern.length){
        return p1 >= str.length;
    }
    if(p1 >= str.length){
        if(p2 + 1 < pattern.length && pattern[p2 + 1] == '*'){
            return matchCore(str, p1, pattern, p2 + 2);
        }else{
            return false;
        }
    }

    //如果p2的后面是“*”
    if(p2 + 1 < pattern.length && pattern[p2 + 1] == '*'){
        if(pattern[p2] == '.' || pattern[p2] == str[p1]){
            //匹配一个字符，接着还可以向后匹配；或者将当前字符和后面的星合起来做空串
            return matchCore(str, p1 + 1, pattern, p2) || matchCore(str, p1, pattern, p2 + 2);
        }else{
            return matchCore(str, p1, pattern, p2 + 2);
        }
    }
    //如果p2的后面不是*
    else{
        if(pattern[p2] == '.' || pattern[p2] == str[p1]){
            return matchCore(str, p1 + 1, pattern, p2 + 1);
        }else{
            return false;
        }
    }
}
复制代码

表示数值的字符串

题目描述

请实现一个函数用来判断字符串是否表示数值（包括整数和小数）。例如，字符串"+100","5e2","-123","3.1416"和"-1E-16"都表示数值。但是"12e","1a3.14","1.2.3","+-5"和"12e+4.3"都不是。

public boolean isNumeric(char[] str) {

}
复制代码

解析

由题式可得出如下约束：

正负号只能出现在第一个位置或者 e/E 后一个位置
e/E 后面有且必须有整数
字符串中只能包含数字、小数点、正负号、 e/E ，其它的都是非法字符
e/E 的前面最多只能出现一次小数点，而 e/E 的后面不能出现小数点

public boolean isNumeric(char[] str) {
    if(str == null || str.length == 0){
        return false;
    }

    boolean signed = false;        //标识是否以正负号开头
    boolean decimal = false;       //标识是否有小数点
    boolean existE = false;        //是否含有e/E
    int start = -1;                //一段连续数字的开头
    int index = 0;                 //从0开始遍历字符

    if(existSignAtIndex(str, 0)){
        signed = true;
        index++;
    }

    while(index < str.length){
        //以下按照index上可能出现的字符进行分支判断
        if(str[index] >= '0' && str[index] <= '9'){
            start = (start == -1) ? index : start;
            index++;

        }else if(str[index] == '+' || str[index] == '-'){
            //首字符的+-我们已经判断过了，因此+-只可能出现在e/E的后面
            if(!existEAtIndex(str, index - 1)){
                return false;
            }
            index++;

        }else if(str[index] == '.'){
            //小数点只可能出现在e/E前面，且只可能出现一次
            //如果出现过小数点了，或者小数点前一段连续数字的前面是e/E
            if(decimal || existEAtIndex(str, start - 1)
               || existEAtIndex(str, start - 2) ){
                return false;
            }
            decimal = true;//出现了小数点
            index++;
            //下一段连续数字的开始
            start = index;

        }else if(existEAtIndex(str, index)){
            if(existE){
                //如果已出现过e/E
                return false;
            }
            existE = true;
            index++;
            //由于e/E后面可能是正负号也可能是数字，所以下一段连续数字的开始不确定
            start = !existSignAtIndex(str, index) ? index : index + 1;

        }else{
            return false;
        }
    }

    //如果最后一段连续数字的开始不存在 -> e/E后面没有数字
    if(start >= str.length){
        return false;
    }

    return true;
}

//在index上的字符是否是e或者E
public boolean existEAtIndex(char[] str, int index){
    if(str == null || str.length == 0 || index < 0 || index > str.length - 1){
        return false;
    }
    return str[index] == 'e' || str[index] == 'E';
}

//在index上的字符是否是正负号
public boolean existSignAtIndex(char[] str, int index){
    if(str == null || str.length == 0 || index < 0 || index > str.length - 1){
        return false;
    }
    return str[index] == '+' || str[index] == '-';
}
复制代码

字符流中第一个只出现一次的字符

题目描述

请实现一个函数用来找出字符流中第一个只出现一次的字符。例如，当从字符流中只读出前两个字符"go"时，第一个只出现一次的字符是"g"。当从该字符流中读出前六个字符“google"时，第一个只出现一次的字符是"l"。

输出描述

如果当前字符流没有存在出现一次的字符，返回#字符。

解析

首先要选取一个容器来保存字符，并且要记录字符进入容器的顺序。如果不考虑中文字符，那么可以使用一张大小为 256 （对应 ASCII 码值范围）的表来保存字符，用字符的 ASCII 码值作为索引，用字符进入容器的次序作为索引对应的记录，表内部维护了一个计数器 position ，每当有字符进入时以该计数器的值作为该字符的次序（初始时，每个字符对应的次序为-1），如果设置该字符的次序时发现之前已设置过（次序不为-1，而是大于等于0），那么将该字符的次序置为-2，表示以后从容器取第一个只出现一次的字符时不考虑该字符。

当从容器取第一个只出现一次的字符时，考虑次序大于等于0的字符，在这个前提下找出次序最小的字符并返回。

//不算中文，保存所有ascii码对应的字符只需256字节，记录ascii码为index的字符首次出现的位置
int[] arr = new int[256];
int position = 0;
{
    for(int i = 0 ; i < arr.length ; i++){
        //初始时所有字符的首次出现的位置为-1
        arr[i] = -1;
    }
}
//Insert one char from stringstream
public void Insert(char ch){
    int ascii = (int)ch;
    if(arr[ascii] == -1){
        arr[ascii] = position++;
    }else if(arr[ascii] >= 0){
        arr[ascii] = -2;
    }
}
//return the first appearence once char in current stringstream
public char FirstAppearingOnce(){
    int minPosi = Integer.MAX_VALUE;
    char res = '#';
    for(int i = 0 ; i < arr.length ; i++){
        if(arr[i] >= 0 && arr[i] < minPosi){
            minPosi = arr[i];
            res = (char)i;
        }
    }

    return res;
}
复制代码

删除链表中重复的结点

题目描述

在一个排序的链表中，存在重复的结点，请删除该链表中重复的结点，重复的结点不保留，返回链表头指针。例如，链表1->2->3->3->4->4->5 处理后为 1->2->5

public ListNode deleteDuplication(ListNode pHead){
    
}
复制代码

解析

此题处理起来棘手的有两个地方：

如果某个结点的后继结点与其重复，那么删除该结点的一串连续重复的结点之后如何删除该结点本身，这就要求我们需要保留当前遍历结点的前驱指针。

但是如果从头结点开始就出现一连串的重复呢？我们又如何删除删除头结点，因此我们需要新建一个辅助结点作为头结点的前驱结点。
在遍历过程中如何区分当前结点是不重复的结点，还是在删除了它的若干后继结点之后最后也要删除它本身的重复结点？这就需要我们使用一个布尔变量记录是否开启了删除模式（ deleteMode ）

经过上述两步分析，我们终于可以安心遍历结点了：

public ListNode deleteDuplication(ListNode pHead){
    if(pHead == null){
        return null;
    }
    ListNode node = new ListNode(Integer.MIN_VALUE);
    node.next = pHead;
    ListNode pre = node, p = pHead;
    boolean deletedMode = false;
    while(p != null){
        if(p.next != null && p.next.val == p.val){
            p.next = p.next.next;
            deletedMode = true;
        }else if(deletedMode){
            pre.next = p.next;
            p = pre.next;
            deletedMode = false;
        }else{
            pre = p;
            p = p.next;
        }
    }

    return node.next;
}
复制代码

二叉树的下一个结点

题目描述

给定一个二叉树和其中的一个结点，请找出中序遍历顺序的下一个结点并且返回。注意，树中的结点不仅包含左右子结点，同时包含指向父结点的指针。

解析

由于中序遍历来到某个结点后，首先会接着遍历它的右子树，如果它没有右子树则会回到祖先结点中将它当做左子树上的结点的那一个，因此有如下分析：

如果当前结点有右子树，那么其后继结点就是其右子树上的最左结点
如果当前结点没有右子树，那么其后继结点就是其祖先结点中，将它当做左子树上的结点的那一个。

public TreeLinkNode GetNext(TreeLinkNode pNode){
    if(pNode == null){
        return null;
    }
    //如果有右子树，后继结点是右子树上最左的结点
    if(pNode.right != null){
        TreeLinkNode p = pNode.right;
        while(p.left != null){
            p = p.left;
        }
        return p;
    }else{
        //如果没有右子树，向上查找第一个当前结点是父结点的左孩子的结点
        TreeLinkNode p = pNode.next;
        while(p != null && pNode != p.left){
            pNode = p;
            p = p.next;
        }

        if(p != null && pNode == p.left){
            return p;
        }
        return null;
    }
}
复制代码

对称的二叉树

题目描述

请实现一个函数，用来判断一颗二叉树是不是对称的。注意，如果一个二叉树同此二叉树的镜像是同样的，定义其为对称的。

boolean isSymmetrical(TreeNode pRoot){
    
｝
复制代码

解析

判断一棵树是否是镜像二叉树，只需将经典的先序遍历序列和变种的 先根再右再左 的先序遍历序列比较，如果相同则为镜像二叉树。

boolean isSymmetrical(TreeNode pRoot){
    if(pRoot == null){
        return true;
    }
    StringBuffer str1 = new StringBuffer("");
    StringBuffer str2 = new StringBuffer("");
    preOrder(pRoot, str1);
    preOrder2(pRoot, str2);
    return str1.toString().equals(str2.toString());
}

public void preOrder(TreeNode root, StringBuffer str){
    if(root == null){
        str.append("#");
        return;
    }
    str.append(String.valueOf(root.val));
    preOrder(root.left, str);
    preOrder(root.right, str);
}

public void preOrder2(TreeNode root, StringBuffer str){
    if(root == null){
        str.append("#");
        return;
    }
    str.append(String.valueOf(root.val));
    preOrder2(root.right, str);
    preOrder2(root.left, str);
}
复制代码

按之字形打印二叉树

题目描述

请实现一个函数按照之字形打印二叉树，即第一行按照从左到右的顺序打印，第二层按照从右至左的顺序打印，第三行按照从左到右的顺序打印，其他行以此类推。

解析

注意下述代码的第 14 行，笔者曾写为 stack2 = stack1 == empty ? stack1 : stack2 ，你能发现错误在哪儿吗？

public ArrayList<ArrayList<Integer>> Print(TreeNode pRoot) {
    ArrayList<ArrayList<Integer>> res = new ArrayList();
    if(pRoot == null){
        return res;
    }

    Stack<TreeNode> stack1 = new Stack();
    Stack<TreeNode> stack2 = new Stack();
    stack1.push(pRoot);
    boolean flag = true;//先加左孩子，再加右孩子
    while(!stack1.empty() || !stack2.empty()){
        Stack<TreeNode> empty = stack1.empty() ? stack1 : stack2;
        stack1 = stack1 == empty ? stack2 : stack1;
        stack2 = empty;
        ArrayList<Integer> row = new ArrayList();
        while(!stack1.empty()){
            TreeNode p = stack1.pop();
            row.add(p.val);
            if(flag){
                if(p.left != null){
                    stack2.push(p.left);
                }
                if(p.right != null){
                    stack2.push(p.right);
                }
            }else{
                if(p.right != null){
                    stack2.push(p.right);
                }
                if(p.left != null){
                    stack2.push(p.left);
                }
            }
        }
        res.add(row);
        flag = !flag;
    }

    return res;
}
复制代码

序列化二叉树

题目描述

请实现两个函数，分别用来序列化和反序列化二叉树

解析

怎么序列化的，就怎么反序列化。这里 deserialize 反序列化时对于序列化到 String[] arr 的哪个结点值来了的变量 index 有两个坑（都是笔者亲自踩的）：

将 index 声明为成员的 int ， Java 中函数调用时不会改变基本类型参数的值的，因此不要企图使用 int 表示当前序列化哪个结点的值来了
之后笔者想用 Integer 代替，但是 Integer 和 String 一样，都是不可变对象，所有的值更改操作在底层都是拆箱和装箱生成新的 Integer ，因此也不要使用 Integer 做序列化到哪一个结点数值来了的计数器
最好使用数组或者自定义的类（在类中声明一个 int 变量）

String Serialize(TreeNode root) {
    if(root == null){
        return "#_";
    }
    //处理头结点、左子树、右子树
    String res = root.val + "_";
    res += Serialize(root.left);
    res += Serialize(root.right);
    return res;
}

TreeNode Deserialize(String str) {
    if(str == null || str.length() == 0){
        return null;
    }
    Integer index = 0;
    return deserialize(str.split("_"), new int[]{0});
}

//怎么序列化的，就怎么反序列化
TreeNode deserialize(String[] arr, int[] index){
    if("#".equals(arr[index[0]])){
        index[0]++;
        return null;
    }
    //头结点、左子树、右子树
    TreeNode root = new TreeNode(Integer.parseInt(arr[index[0]]));
    index[0]++;
    root.left = deserialize(arr, index);
    root.right = deserialize(arr, index);
    return root;
}
复制代码

二叉搜索树的第k个结点

题目描述

给定一棵二叉搜索树，请找出其中的第k小的结点。例如，（5，3，7，2，4，6，8）中，按结点数值大小顺序第三小结点的值为4。

TreeNode KthNode(TreeNode pRoot, int k){
    
}
复制代码

解析

二叉搜索树的特点是，它的中序序列是有序的，因此我们可以借助中序遍历在递归体中第二次来到当前结点时更新一下计数器，直到遇到第k个结点保存并返回即可。

值得注意的地方是：

int[]

TreeNode KthNode(TreeNode pRoot, int k){
    if(pRoot == null){
        return null;
    }
    TreeNode[] res = new TreeNode[1];
    inOrder(pRoot, new int[]{ k }, res);
    return res[0];
}

public void inOrder(TreeNode root, int[] count, TreeNode[] res){
    if(root == null){
        return;
    }
    inOrder(root.left, count, res);
    count[0]--;
    if(count[0] == 0){
        res[0] = root;
        return;
    }
    inOrder(root.right, count, res);
}
复制代码

如果可以利用我们熟知的算法，比如本题中的中序遍历。管它三七二十一先将熟知方法写出来，然后再按具体的业务需求对其进行改造（包括返回值、参数列表，但一般不会更改遍历算法的返回值）

数据流的中位数

题目描述

如何得到一个数据流中的中位数？如果从数据流中读出奇数个数值，那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值，那么中位数就是所有数值排序之后中间两个数的平均值。我们使用Insert()方法读取数据流，使用GetMedian()方法获取当前读取数据的中位数。

public void Insert(Integer num) {
    
}

public Double GetMedian() {
    
}
复制代码

解析

由于中位数只与排序后位于数组中间的一个数或两个数相关，而与数组两边的其它数无关，因此我们可以用一个大根堆保存数组左半边的数的最大值，用一个小根堆保存数组右半边的最小值，插入元素 O(logn) ，取中位数 O(1) 。

public class Solution {

    //小根堆、大根堆
    PriorityQueue<Integer> minHeap = new PriorityQueue(new MinRootHeadComparator());
    PriorityQueue<Integer> maxHeap = new PriorityQueue(new MaxRootHeadComparator());
    int count = 0;

    class MaxRootHeadComparator implements Comparator<Integer>{
        //返回值大于0则认为逻辑上i2大于i1（无关对象包装的数值）
        public int compare(Integer i1, Integer i2){
            return i2.intValue() - i1.intValue();
        }
    }

    class MinRootHeadComparator implements Comparator<Integer>{
        public int compare(Integer i1, Integer i2){
            return i1.intValue() - i2.intValue();
        }
    }

    public void Insert(Integer num) {
        count++;//当前这个数是第几个进来的
        //编号是奇数就放入小根堆（右半边），否则放入大根堆
        if(count % 2 != 0){
            //如果要放入右半边的数比左半边的最大值要小则需调整左半边的最大值放入右半边并将当前这个数放入左半边，这样才能保证右半边的数都比左半边的大
            if(maxHeap.size() > 0 && num < maxHeap.peek()){
                maxHeap.add(num);
                num = maxHeap.poll();
            }
            minHeap.add(num);
        }else{
            if(minHeap.size() > 0 && num > minHeap.peek()){
                minHeap.add(num);
                num = minHeap.poll();
            }
            maxHeap.add(num);
        }
    }

    public Double GetMedian() {
        if(count == 0){
            return 0.0;
        }
        if(count % 2 != 0){
            return minHeap.peek().doubleValue();
        }else{
            return (minHeap.peek().doubleValue() + maxHeap.peek().doubleValue()) / 2;
        }
    }
}
复制代码

滑动窗口的最大值

题目描述

给定一个数组和滑动窗口的大小，找出所有滑动窗口里数值的最大值。例如，如果输入数组{2,3,4,2,6,2,5,1}及滑动窗口的大小3，那么一共存在6个滑动窗口，他们的最大值分别为{4,4,6,6,6,5}；针对数组{2,3,4,2,6,2,5,1}的滑动窗口有以下6个： {[2,3,4],2,6,2,5,1}， {2,[3,4,2],6,2,5,1}， {2,3,[4,2,6],2,5,1}， {2,3,4,[2,6,2],5,1}， {2,3,4,2,[6,2,5],1}， {2,3,4,2,6,[2,5,1]}。

public ArrayList<Integer> maxInWindows(int [] num, int size){
    
}
复制代码

解析

使用一个单调非增队列，队头保存当前窗口的最大值，后面保存在窗口移动过程中导致队头失效（出窗口）后的从而晋升为窗口最大值的候选值。

public ArrayList<Integer> maxInWindows(int [] num, int size){
    ArrayList<Integer> res = new ArrayList();
    if(num == null || num.length == 0 || size <= 0 || size > num.length){
        return res;
    }

    //用队头元素保存窗口最大值，队列中元素只能是单调递减的，窗口移动可能导致队头元素失效
    LinkedList<Integer> queue = new LinkedList();
    int start = 0, end = size - 1;
    for(int i = start ; i <= end ; i++){
        addLast(queue, num[i]);
    }
    res.add(queue.getFirst());
    //移动窗口
    while(end < num.length - 1){
        addLast(queue, num[++end]);
        if(queue.getFirst() == num[start]){
            queue.pollFirst();
        }
        start++;
        res.add(queue.getFirst());
    }

    return res;
}

public void addLast(LinkedList<Integer> queue, int num){
    if(queue == null){
        return;
    }
    //加元素之前要确保该元素小于等于队尾元素
    while(queue.size() != 0 && num > queue.getLast()){
        queue.pollLast();
    }
    queue.addLast(num);
}
复制代码

矩形中的路径

题目描述

请设计一个函数，用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始，每一步可以在矩阵中向左，向右，向上，向下移动一个格子。如果一条路径经过了矩阵中的某一个格子，则之后不能再次进入这个格子。例如 a b c e s f c s a d e e 这样的3 X 4 矩阵中包含一条字符串"bcced"的路径，但是矩阵中不包含"abcb"路径，因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后，路径不能再次进入该格子。

解析

定义一个黑盒 hasPathCorechar(matrix, rows, cols, int i, int j, str, index) ，表示从 rows 行 cols 列的矩阵 matrix 中的 (i,j) 位置开始走是否能走出一条与 str 的子串 index ~ str.length-1 相同的路径。那么对于当前位置 (i,j) ，需要关心的只有一下三点：

(i,j) 是否越界了
(i,j) 上的字符是否和 str[index] 匹配
(i,j) 是否已在之前走过的路径上

如果通过了上面三点检查，那么认为 (i,j) 这个位置是可以走的，剩下的就是 (i,j) 上下左右四个方向能否走出 str 的 index+1 ~ str.length-1 ，这个交给黑盒就好了。

还有一点要注意，如果确定了可以走当前位置 (i,j) ，那么需要将该位置的 visited 标记为 true ，表示该位置在已走过的路径上，而退出 (i,j) 的时候（对应下面第 32 行）又要将他的 visited 重置为 false 。

public boolean hasPath(char[] matrix, int rows, int cols, char[] str){
    if(matrix == null || matrix.length != rows * cols || str == null){
        return false;
    }
    boolean[] visited = new boolean[matrix.length];
    for(int i = 0 ; i < rows ; i++){
        for(int j = 0 ; j < cols ; j++){
            //以矩阵中的每个点作为起点尝试走出str对应的路径
            if(hasPathCore(matrix, rows, cols, i, j, str, 0, visited)){
                return true;
            }
        }
    }
    return false;
}

//当前在矩阵的(i,j)位置上
//index -> 匹配到了str中的第几个字符
private boolean hasPathCore(char[] matrix, int rows, int cols, int i, int j, 
                            char[] str, int index, boolean[] visited){
    if(index == str.length){
        return true;
    }
    //越界或字符不匹配或该位置已在路径上
    if(!match(matrix, rows, cols, i, j, str[index]) || visited[i * cols + j] == true){
        return false;
    }
    visited[i * cols + j] = true;
    boolean res = hasPathCore(matrix, rows, cols, i + 1, j, str, index + 1, visited) ||
        hasPathCore(matrix, rows, cols, i - 1, j, str, index + 1, visited) ||
        hasPathCore(matrix, rows, cols, i, j + 1, str, index + 1, visited) ||
        hasPathCore(matrix, rows, cols, i, j - 1, str, index + 1, visited);
    visited[i * cols + j] = false;
    return res;
}

//矩阵matrix中的(i,j)位置上是否是c字符
private boolean match(char[] matrix, int rows, int cols, int i, int j, char c){
    if(i < 0 || i > rows - 1 || j < 0 || j > cols - 1){
        return false;
    }
    return matrix[i * cols + j] == c;
}
复制代码

机器人的运动范围

题目描述

地上有一个m行和n列的方格。一个机器人从坐标0,0的格子开始移动，每一次只能向左，右，上，下四个方向移动一格，但是不能进入行坐标和列坐标的数位之和大于k的格子。例如，当k为18时，机器人能够进入方格（35,37），因为3+5+3+7 = 18。但是，它不能进入方格（35,38），因为3+5+3+8 = 19。请问该机器人能够达到多少个格子？

解析

定义一个黑盒 walk(int threshold, int rows, int cols, int i, int j, boolean[] visited) ，它表示统计从 rows 行 cols 列的矩阵中的 (i,j) 开始所能到达的格子并返回，对于当前位置 (i,j) 有如下判断：

(i,j) 是否越界矩阵了
(i,j) 是否已被统计过了
(i,j) 的行坐标和列坐标的数位之和是否大于 k

如果通过了上面三重检查，则认为 (i,j) 是可以到达的（ res=1 ），并标记 (i,j) 的 visited 为 true 表示已被统计过了，然后对 (i,j) 的上下左右的格子调用黑盒进行统计。

这里要注意的是，与上一题不同， visited 不会在递归计算完子状态后被重置回 false ，因为每个格子只能被统计一次。 visited 的含义不一样

public int movingCount(int threshold, int rows, int cols){
    if(threshold < 0 || rows < 0 || cols < 0){
        return 0;
    }
    boolean[] visited = new boolean[rows * cols];
    return walk(threshold, rows, cols, 0, 0, visited);
}

private int walk(int threshold, int rows, int cols, int i, int j, boolean[] visited){
    if(!isLegalPosition(rows, cols, i, j) || visited[i * cols + j] == true
       || bitSum(i) + bitSum(j) > threshold){
        return 0;
    }
    int res = 1;
    visited[i * cols + j] = true;
    res += walk(threshold, rows, cols, i + 1, j, visited) +
        walk(threshold, rows, cols, i - 1, j, visited) +
        walk(threshold, rows, cols, i, j + 1, visited) +
        walk(threshold, rows, cols, i, j - 1, visited);
    return res;
}

private boolean isLegalPosition(int rows, int cols, int i, int j){
    if(i < 0 || j < 0 || i > rows - 1 || j > cols - 1){
        return false;
    }
    return true;
}

public int bitSum(int num){
    int res = num % 10;
    while((num /= 10) != 0){
        res += num % 10;
    }
    return res;
}
复制代码

原文 https://juejin.im/post/5c6b9bad518825266c3f064f

正文到此结束