转载

304. Range Sum Query 2D - Immutable

Given a 2D matrix matrix, find the sum of the elements inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

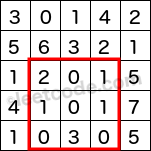
The above rectangle (with the red border) is defined by (row1, col1) = (2, 1) and (row2, col2) = (4, 3), which contains sum = 8.

Example:

Given matrix = [
  [3, 0, 1, 4, 2],
  [5, 6, 3, 2, 1],
  [1, 2, 0, 1, 5],
  [4, 1, 0, 1, 7],
  [1, 0, 3, 0, 5]
]

sumRegion(2, 1, 4, 3) -> 8
sumRegion(1, 1, 2, 2) -> 11
sumRegion(1, 2, 2, 4) -> 12

Note:

You may assume that the matrix does not change.

There are many calls to sumRegion function.

You may assume that row1 ≤ row2 and col1 ≤ col2.

难度：medium

题目：给定二维矩阵，找出方框内所包含元素的各，方框由左上角与右下角座标表示。

思路：求出（0,0)到(i,j)所有元素之和。(x1, y1, x2, y2) = (x2, y2) + (x1 - 1, y1 - 1) - (x1 - 1, y2) - (x2, y1 - 1)

Runtime: 60 ms, faster than 100.00% of Java online submissions for Range Sum Query 2D - Immutable.

Memory Usage: 48.7 MB, less than 16.67% of Java online submissions for Range Sum Query 2D - Immutable.

class NumMatrix {
    private int[][] matrix;
    public NumMatrix(int[][] matrix) {
        this.matrix = matrix;
        for (int i = 0; i < matrix.length; i++) {
            for (int j = 1; j < matrix[i].length; j++) {
                matrix[i][j] += matrix[i][j - 1];
            }
        }
        for (int i = 1; i < matrix.length; i++) {
            for (int j = 0; j < matrix[i].length; j++) {
                matrix[i][j] += matrix[i - 1][j];
            }
        }
    }
    
    public int sumRegion(int row1, int col1, int row2, int col2) {
        int rightUp = (row1 - 1 >= 0) ? matrix[row1 - 1][col2] : 0;
        int leftTop = (row1 - 1 >= 0 && col1 - 1 >= 0) ? matrix[row1 - 1][col1 - 1] : 0;
        int leftBottom = (col1 - 1 >= 0) ? matrix[row2][col1 - 1] : 0;
        
        return matrix[row2][col2] + leftTop - rightUp - leftBottom;
    }
}

/**
 * Your NumMatrix object will be instantiated and called as such:
 * NumMatrix obj = new NumMatrix(matrix);
 * int param_1 = obj.sumRegion(row1,col1,row2,col2);
 */

原文 https://segmentfault.com/a/1190000018313699

正文到此结束