转载

Java中的冒泡排序算法实例

冒泡排序是一种奇特的算法，它既是最流行的排序算法之一也是性能最差的排序算法之一。冒泡排序的平均案例性能为O（n ^ 2），这意味着随着数组大小的增长，排序该数组所需的时间将增加二次方。由于这个原因，在生产代码中不使用冒泡排序，而是优先选择快速排序和合并排序。实际上，Java自己的Arrays.sort（）方法，是在Java中对数组进行排序的最简单方法，它还使用两个pivot快速排序来对基元数组进行排序，用稳定的合并排序算法对对象数组进行排序。

这种算法性能低下的原因是过度比较和交换，因为它将数组的每个元素与另一个元素进行比较，如果在右侧则交换。

由于它的二次性能，冒泡排序最适合于小的，几乎排序的列表，例如{1,2,4,3,5}，只需要进行一次交换。具有讽刺意味的是，冒泡排序的最佳性能，即O（n）击败了快速排序的O（NlogN）的最佳性能。

有人可能会争辩说，为什么要教一个性能那么差的算法，为什么不教插入或选择排序，它和冒泡排序一样简单，而且性能更好。恕我直言，算法的简易性不仅取决于算法本身，还取决于程序员。

许多程序员会发现插入排序比冒泡排序更容易，但是会有很多人会发现更容易记住的冒泡排序。尽管他们中的许多人在现实生活中不知不觉地使用插入排序，例如在手中整理扑克牌。

学习这种排序算法的另一个原因是用于比较分析，如何改进算法，如何为相同的问题提出不同的算法。简而言之，尽管存在各种缺点，但冒泡排序仍然是最流行的算法。

在本教程中，我们将学习冒泡排序的工作原理，冒泡排序算法的复杂性和性能，Java中的实现和源代码以及冒泡排序的分步示例。

冒泡排序算法的工作原理

就像气泡从水中出现一样，在气泡排序中最小或最大数字，取决于您是按升序还是降序排序数组，气泡朝着数组的开始或结束冒出。我们至少需要n次传递来对数组进行完全排序，并且在每个传递的末尾，一个元素被排序到其正确的位置。您可以从数组中提取第一个元素，并开始将其与其他元素进行比较，交换小于您要比较的数字的元素。您可以从开始或结束进行比较，正如我们在气泡排序示例中从结束对元素进行比较一样。让我们看一个循序渐进的例子，让我们看一个循序渐进的例子，使用冒泡排序对数组进行排序。

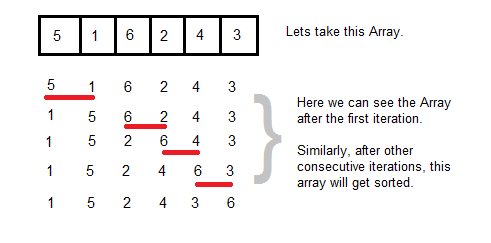
Java中的冒泡排序算法实例

在这个数组中，我们从索引0（即5）开始，并从开始到结束对元素进行比较。因此，我们比较的第一个元素是1，因为5大于1，所以我们交换它们（因为按升序排序的数组在末尾将有更大的数字）。接下来我们比较5到6，这里没有交换，因为6大于5，并且它在高于5的索引上。现在我们将6与2进行比较，再次需要交换以将6移向末尾。在这一过程的末尾，6到达（气泡上升）数组的顶部。在下一个迭代中，5将按其位置排序，在n次迭代之后，所有元素都将排序。由于我们将每个元素与另一个元素进行比较，因此需要两个for循环，这会导致o（n^2）的复杂性。

冒泡排序算法流程图

理解算法的另一个很酷的方法是绘制它的流程图。它将遍历循环中的每个迭代以及在算法执行期间如何做出决策。这是我们的冒泡排序算法的流程图，它补充了我们对这种排序算法的实现。

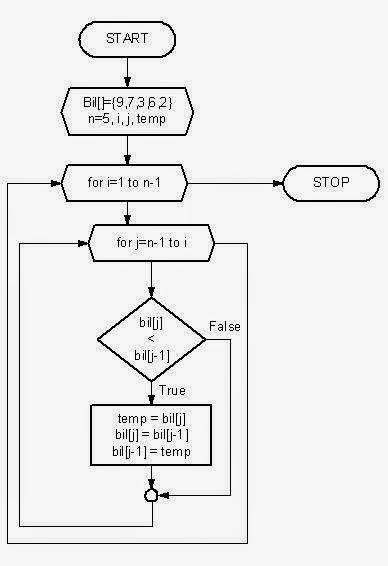
Java中的冒泡排序算法实例

这里我们有整数数组{9,7,3,6,2}，从四个变量i，j，temp和数组长度开始，它存储在变量n中。我们有两个for循环，外循环运行从1到n-1。我们的内循环从n-1到i。许多程序员在这里犯了错误，如果您使用第二个元素开始外部循环，而不是确保在内部循环上使用j>=i条件，或者如果您使用第一个元素（例如i=0）开始，请确保使用j>i 来避arrayindexoutofbound异常。现在我们比较每个元素并交换它们以将更小的元素移向数组的前面。如我所说，根据您的导航方向，第一遍中最大的元素将按最高索引排序，或者最小的元素将按最低索引排序。在这种情况下，在第一次通过后，将对最小的数字进行排序。这个循环一直运行到j>=i，然后结束，i 变成i+1。整个过程将重复，直到外部循环完成，然后对数组进行排序。在流程图中，菱形框用于决策，相当于代码中的if-else语句。您可以在这里看到决策框在内部循环中，这意味着我们在每个迭代中都要进行N次比较，总计NxN个比较。

冒泡排序算法的复杂性和性能

正如我之前所说的，与其他排序算法（如快速排序，合并排序或shell排序）相比，冒泡排序表现不佳。这些算法的平均情况复杂度为O（NLogN），而冒泡排序平均情况复杂度为O（n ^ 2）。具有讽刺意味的是，在最佳情况下，冒泡排序比具有O（n）性能的快速排序更好。冒泡排序比quicksort或mergesort慢三倍，即使n = 100，但它更容易实现和记忆。这里是冒泡排序性能和复杂性的摘要：

冒泡排序最差情况性能O（n ^ 2）

冒泡排序最佳情况性能O（n）

冒泡排序平均情况性能O（n ^ 2）

您可以进一步探索插入排序和选择排序，它也会以类似的时间复杂度进行排序。您不仅可以使用冒泡排序，还可以使用ArrayList或任何其他集合类对数组进行排序。虽然你真的应该使用Arrays.sort（）或Collections.sort（）来实现这些目的。

Java中的冒泡排序实现

这是使用Java实现冒泡排序算法的程序。不要惊讶于导入java.util.Array，这里我们没有使用它的排序方法，而是使用它以可读格式打印数组。我已经创建了一个交换函数来交换数字和提高代码的可读性，如果你不喜欢，可以在内部循环语句if内部的swap方法中内联代码。虽然我已经使用main方法进行测试，但为了更好地展示，我建议你为冒泡实现编写一些单元测试用例。

import java.util.Arrays;
 
/**
* Java program to implement bubble sort algorithm and sort integer array using
* that method.
*
* @author Javin Paul
*/<font>
<b>public</b> <b>class</b> BubbleSort{
 
   <b>public</b> <b>static</b> <b>void</b> main(String args[]) {
        bubbleSort(<b>new</b> <b>int</b>[] { 20, 12, 45, 19, 91, 55 });
        bubbleSort(<b>new</b> <b>int</b>[] { -1, 0, 1 });
        bubbleSort(<b>new</b> <b>int</b>[] { -3, -9, -2, -1 });

    }

    </font><font><i>/*
     * This method sort the integer array using bubble sort algorithm
     */</i></font><font>
    <b>public</b> <b>static</b> <b>void</b> bubbleSort(<b>int</b>[] numbers) {
        System.out.printf(</font><font>"Unsorted array in Java :%s %n"</font><font>, Arrays.toString(numbers));

        <b>for</b> (<b>int</b> i = 0; i < numbers.length; i++) {
            <b>for</b> (<b>int</b> j = numbers.length -1; j > i; j--) {
                <b>if</b> (numbers[j] < numbers[j - 1]) {
                    swap(numbers, j, j-1);
                }
            }
        }

        System.out.printf(</font><font>"Sorted Array using Bubble sort algorithm :%s %n"</font><font>,
                Arrays.toString(numbers));
    }
    
    </font><font><i>/*
     * Utility method to swap two numbers in array
     */</i></font><font>
    <b>public</b> <b>static</b> <b>void</b> swap(<b>int</b>[] array, <b>int</b> from, <b>int</b> to){
        <b>int</b> temp = array[from];
        array[from] = array[to];
        array[to] = temp;
    }
 
}
 
 
Output
Unsorted array in Java : [20, 12, 45, 19, 91, 55]
Sorted Array using Bubble sort algorithm : [12, 19, 20, 45, 55, 91]
Unsorted array in Java : [-1, 0, 1]
Sorted Array using Bubble sort algorithm : [-1, 0, 1]
Unsorted array in Java : [-3, -9, -2, -1]
Sorted Array using Bubble sort algorithm : [-9, -3, -2, -1]
</font>

如何改进冒泡排序算法

在面试中，一个普遍的后续问题是如何改进特定算法，而冒泡排序也正如此。为了改进任何算法，您必须了解该算法的每个步骤是如何工作的，然后只有您能够发现代码中的任何缺陷。如果按照本教程，您将发现数组是通过将元素移动到其正确位置来排序的。在最坏的情况下，如果数组是反向排序，那么我们需要移动每个元素，这将需要n-1次过程，每次过程有n-1次比较和n-1次交换，但如果数组已经排序，最佳情况是：现有的冒泡排序方法仍将采用n-1个过程，相同的比较次数，但没有交换。如果仔细观察，你会发现在一次通过数组后，最大的元素将移动到数组的末尾，许多其他元素也会移动到正确的位置。通过利用此属性，可以推断在传递过程中，如果没有一对连续的条目顺序不对，那么数组将被排序。我们当前的算法没有利用这个属性。如果我们跟踪交换，那么我们可以决定是否需要对数组进行额外的迭代。这是Bubble Sort算法的改进版本，当数组已经排序时，在最佳情况下只需要1次迭代和n-1次比较。与我们现有的N-1次传递方法相比，这也将改善Bubble sort的平均案例性能。

  <font><i>/*
     * An improved version of Bubble Sort algorithm, which will only do
     * 1 pass and n-1 comparison if array is already sorted. 
     */</i></font><font>
    <b>public</b> <b>static</b> <b>void</b> bubbleSortImproved(<b>int</b>[] number) {        
        <b>boolean</b> swapped = <b>true</b>;
        <b>int</b> last = number.length - 2;

        </font><font><i>// only continue if swapping of number has occurred</i></font><font>
        <b>while</b> (swapped) {
            swapped = false;
            
            <b>for</b> (<b>int</b> i = 0; i <= last; i++) {
                <b>if</b> (number[i] > number[i + 1]) {
                    
                    </font><font><i>// pair is out of order, swap them</i></font><font>
                    swap(number, i, i + 1);
                    
                    swapped = <b>true</b>; </font><font><i>// swapping occurred</i></font><font>
                }
            }

            </font><font><i>// after each pass largest element moved to end of array</i></font><font>
            last--;
        }

    }
</font>

现在让我们用两个输入测试这个方法，一个是数组排序（最佳情况），另一个是只有一对无序。如果我们将int数组{10,20,30,40,50,60}传递给这个方法，最初将在循环中进入并使swapped = false。然后它将进入循环。当i = 0时，它会将数字与数字[i + 1]进行比较，即10到20，并检查是否10> 20，因为不大于，它就不会进入内部，并且不会发生交换。当i=1时，将再次比较20>30不交换，下一次当i=2， 30>40为假，不再交换，下一次i=3，40>50为假，所以不交换。现在最后一对比较i=4，它将再次比较50>60，这是错误的，所以如果阻止不进行交换，控件将不会进入。因为交换始终为假，并且在循环再次进行时控件不会进入。所以你知道你的数组在一次传递之后就被排序了。

现在考虑另一个例子，其中只有一对乱序，假设字符串数组名= {“Ada”，“C ++”，“Lisp”，“Java”，“Scala”}，这里只有一对乱序例如“Lisp”应该出现在“Java”之后。让我们看看我们改进的冒泡排序算法如何在这里工作。在第一遍中，比较将继续而不进行交换，直到我们比较“Lisp”和“Java”，这里“Lisp”.compareTo（“Java”）> 0将变为true并且将发生交换，这意味着Java将转到Lisp位置，Lisp将占据Java的位置。这将使boolean变量swapped = true，现在在这个传递的最后比较中，我们将“Lisp”与“Scala”进行比较，并且再次没有交换。现在我们将最后一个索引减少1，因为Scala在最后位置排序，不会进一步参与。但现在交换的变量是真的，所以控件将再次进入while循环和for循环，但这次不会进行交换，所以不会进行另一次传递。与早期实现的N-1次传递相比，我们的数组现在只进行了两次传递。在平均情况下，这种冒泡排序实现要比选择排序算法好得多，甚至表现更好，因为现在排序与元素总数不成比例，但只与乱序对的数量成比例。

顺便说一下，使用冒泡排序对String数组进行排序，需要重载BubbleSortImproved（）方法来接受String []，还需要使用compareTo（）方法按字典顺序比较两个String对象。这是使用冒泡排序对String数组进行排序的Java程序：

<b>import</b> java.util.Arrays;

<b>class</b> BubbleSortImproved {

    <b>public</b> <b>static</b> <b>void</b> main(String args[]) {

        String[] test = {<font>"Ada"</font><font>, </font><font>"C++"</font><font>, </font><font>"Lisp"</font><font>, </font><font>"Java"</font><font>, </font><font>"Scala"</font><font>};
        System.out.println(</font><font>"Before Sorting : "</font><font> + Arrays.toString(test));
        bubbleSortImproved(test);
        System.out.println(</font><font>"After Sorting : "</font><font> + Arrays.toString(test));
    }

    </font><font><i>/*
     * An improved implementation of Bubble Sort algorithm, which will only do
     * 1 pass and n-1 comparison if array is already sorted. 
     */</i></font><font>
    <b>public</b> <b>static</b> <b>void</b> bubbleSortImproved(String[] names) {        
        <b>boolean</b> swapped = <b>true</b>;
        <b>int</b> last = names.length - 2;

        </font><font><i>// only continue if swapping of number has occurred</i></font><font>
        <b>while</b> (swapped) {
            swapped = false;
            
            <b>for</b> (<b>int</b> i = 0; i <= last; i++) {
                <b>if</b> (names[i].compareTo(names[i + 1]) > 0) {
                    
                    </font><font><i>// pair is out of order, swap them</i></font><font>
                    swap(names, i, i + 1);
                    
                    swapped = <b>true</b>; </font><font><i>// swapping occurred</i></font><font>
                }
            }

            </font><font><i>// after each pass largest element moved to end of array</i></font><font>
            last--;
        }

    }

    <b>public</b> <b>static</b> <b>void</b> swap(String[] names, <b>int</b> fromIdx, <b>int</b> toIdx) {
        String temp = names[fromIdx]; </font><font><i>// exchange</i></font><font>
        names[fromIdx] = names[toIdx];
        names[toIdx] = temp;
    }

}

Output:
Before Sorting : [Ada, C++, Lisp, Java, Scala]
After Sorting : [Ada, C++, Java, Lisp, Scala]
</font>

选择排序vs冒泡排序哪个更好？

尽管在最坏的情况下，选择排序和冒泡排序都具有O（n^2）的复杂性。平均而言，我们希望冒泡排序比选择排序执行得更好，因为冒泡排序会比选择排序更快完成排序，这是因为在相同数量的比较中有更多的数据移动，因为我们在气泡排序上成对比较元素。如果我们使用改进的冒泡排序然后布尔测试不进入while循环，当数组被排序时也将有所帮助。如我所说，气泡排序的最坏情况发生在原始数组按降序排列时，而在最佳情况下，如果原始数组已排序，气泡排序将只执行一次，而选择排序将执行n-1次。考虑到这一点，我认为气泡排序比选择排序平均要好。

这就是Java中的冒泡排序问题。我们已经了解了冒泡排序算法的工作原理，以及如何在Java中实现它。它是最简单的排序算法之一，而且很容易记住，但是除了学术和数据结构以及算法培训课程之外，它没有任何实际用途。最糟糕的情况是，性能是二次的，这意味着它不适合大型数组或列表。如果必须使用冒泡排序，它最适合于已经排序的小型数组，在这种情况下，它进行非常少的交换，其性能可能是O（N）。

原文 https://www.jdon.com/51847

正文到此结束