第九届蓝桥杯Java B——测试次数
x星球的居民脾气不太好，但好在他们生气的时候唯一的异常举动是：摔手机。
各大厂商也就纷纷推出各种耐摔型手机。x星球的质监局规定了手机必须经过耐摔测试，并且评定出一个耐摔指数来，之后才允许上市流通。
x星球有很多高耸入云的高塔，刚好可以用来做耐摔测试。塔的每一层高度都是一样的，与地球上稍有不同的是，他们的第一层不是地面，而是相当于我们的2楼。
如果手机从第7层扔下去没摔坏，但第8层摔坏了，则手机耐摔指数=7。
特别地，如果手机从第1层扔下去就坏了，则耐摔指数=0。
如果到了塔的最高层第n层扔没摔坏，则耐摔指数=n
为了减少测试次数，从每个厂家抽样3部手机参加测试。
某次测试的塔高为1000层，如果我们总是采用最佳策略，在最坏的运气下最多需要测试多少次才能确定手机的耐摔指数呢？
请填写这个最多测试次数
我们把$M$层楼 / $N$个手机的问题转化成一个函数$F(M,N)$，其中楼层数$M$和手机数$N$是函数的两个参数，而函数的值则是最优解的最大尝试次数
假设我们第一个手机扔出的位置在第$X/ (1 /leq X /leq M)$层，会出现两种情况
- 第一个手机没碎，那么剩余的$M-X$层楼，剩余$N$个手机，可以转变为函数：$F(M-X,N)+ 1,1/leq X/leq M$
- 第一个手机碎了，那么只剩下从$1$层到$X-1$层楼需要尝试，剩余的手机数量是$N-1$，可以转变为函数：$F(X-1,N-1) + 1,1/leq X/leq M$
整体而言，我们要求出的是$M$层楼 / $N$个手机的条件下，最大尝试次数最小的解，所以这个题目的状态转移方程式如下：
$$
F(M,N) = Min(Max(F(M-X,N) + 1,F(X-1，N-1) + 1)),1/leq X/leq M
$$
根据动态规划状态转移方程是和自底向上的求解思路，我们需要从1个手机1层楼的最优尝试次数，一步一步推导后续的状态，直到计算出3个手机4层楼的尝试次数为止
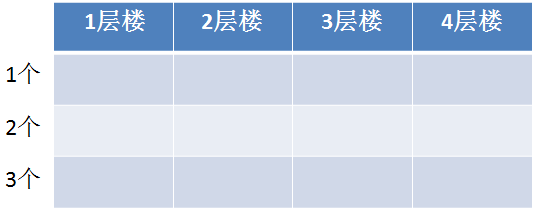
首先我们可以填充第一个手机在各个楼层的尝试次数，以及任意多手机在1层楼的尝试次数
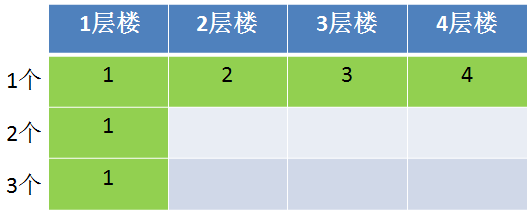
2个手机2层楼的情况就需要带入状态转移方程式了
$$
F(2,2) = Min(Max(F(2-X,2) + 1,F(X-1,2-1) + 1))，1/leq X/leq 2
$$
因为$X$的取值是1和2，我们需要对$X$的值逐一来尝试，计算过程就不展示了，给出结果是$F(2,2)=2$
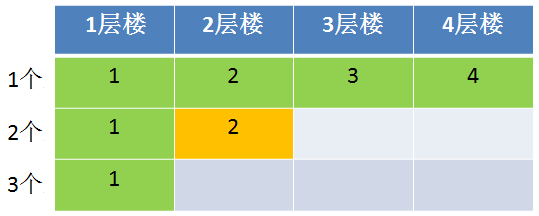
接下来我们看一看2个手机3层楼的情况：
$$ F(2,3) = Min(Max(F(3-X,2) + 1, F(X-1,2-1) + 1)),1/leq X/leq 3 $$
正文到此结束
热门推荐
相关文章
近期评论
-
666
-
文章和留言都翻到11页了 没有OOM
-
-
朋友，翻页到11页，及以后，会出现OOM，无法访问
-
-
-
-
版本号是多少，你可以下载哪个代码仓库，jdk选1.8 直接跑就行
-
-
Loading...
![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)
