转载

第九届蓝桥杯Java B——螺旋折线

如下图所示的螺旋折线经过平面上所有整点恰好一次。

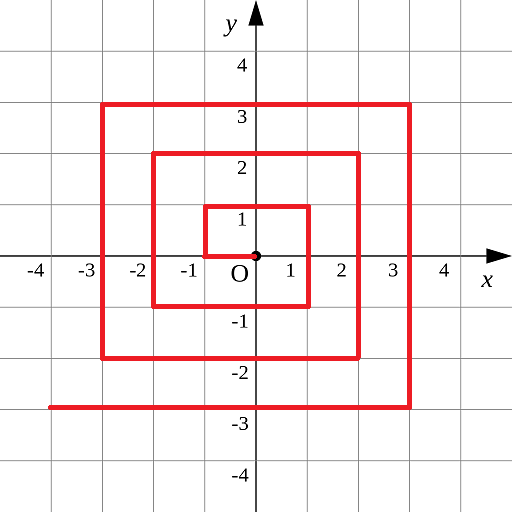
对于整点(X, Y)，我们定义它到原点的距离dis(X, Y)是从原点到(X, Y)的螺旋折线段的长度。

例如dis(0, 1)=3, dis(-2, -1)=9

给出整点坐标(X, Y)，你能计算出dis(X, Y)吗？

【输入格式】

X和Y

对于40%的数据，-1000 <= X, Y <= 1000

对于70%的数据，-100000 <= X， Y <= 100000

对于100%的数据, -1000000000 <= X, Y <= 1000000000

【输出格式】

输出dis(X, Y)

【输入样例】

0 1

【输出样例】

资源约定：

峰值内存消耗（含虚拟机） < 256M

CPU消耗 < 1000ms

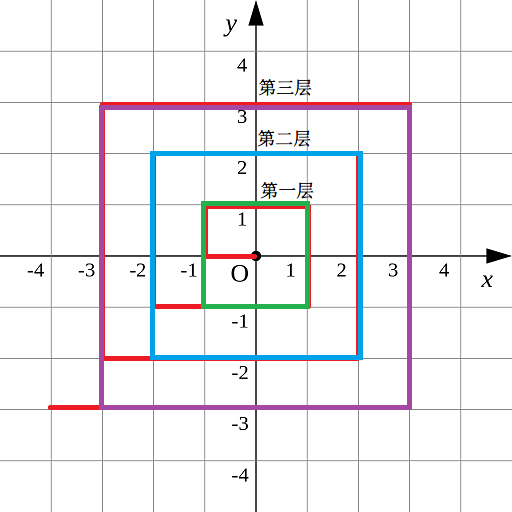
第九届蓝桥杯Java B——螺旋折线

假设要求的坐标是$(x,y)$，那么根据上面的图就可以把$(x,y)$所在的层数确定，$layer = max(abs(x),abs(y))$，确定层数以后，前面所有层的线段和就确定了，假设$(x,y)$在第$n$层，那么前面$n-1$层正方形线段和就是$4/times (n + 1)/times n$

接着再看$(x,y)$这个坐标是第$n$层的第几个。我们可以认为第$i$层的起始点坐标是$(-i, -i + 1$，那么求得$(x,y)$到起始点之间的距离之后还要加上1

import java.util.Scanner;

public class Main {

    public static void main(String[] args) {
        Scanner cin = new Scanner(System.in);
        long x = cin.nextLong();
        long y = cin.nextLong();
        long layer = Math.max(Math.abs(x), Math.abs(y));
        long startx = -layer;
        long starty = -layer + 1;
        long sum = (layer * (layer - 1)) << 2;
        sum += Math.abs(x - startx) + Math.abs(y - starty) + 1;
        System.out.println(sum);
    }
}

原文 https://www.wmathor.com/index.php/archives/1293/

正文到此结束