JDK源码那些事儿之红黑树基础上篇
说到HashMap,就一定要说到红黑树,红黑树作为一种自平衡二叉查找树,是一种用途较广的数据结构,在jdk1.8中使用红黑树提升HashMap的性能,今天就来说一说红黑树。
前言
限于篇幅,本文只对红黑树的基础进行说明,暂不涉及源码部分,大部分摘抄自维基百科,这里也贴出对应链接:
维基百科(中文): https://zh.wikipedia.org/wiki...
维基百科: https://en.wikipedia.org/wiki...
笔者这里会根据维基百科的讲解做些说明,方便初学者理解。
定义
当然,在了解红黑树之前,先回顾下树这种结构的特点(来自 维基百科 )):
每个节点都只有有限个子节点或无子节点;
没有父节点的节点称为根节点;
每一个非根节点有且只有一个父节点;
除了根节点外,每个子节点可以分为多个不相交的子树;
树里面没有环路(cycle)
红黑树(英语:Red–black tree)是一种 自平衡二叉查找树 ,红黑树和AVL树一样都对插入时间、删除时间和查找时间提供了最好可能的最坏情况担保。
红黑树的结构复杂,但它的操作有着良好的最坏情况运行时间,并且在实践中高效:它可以在O(log n)时间内完成查找,插入和删除,这里的O(log n) n是树中元素的数目。
这些描述说明了红黑树结构的一大特点:在增删查上即使是最坏的一种数据结构情况,也保证了性能。
有些新手可能会想,为什么能保证?
看完整篇文章,你可能就会了解清楚,红黑树概念上其实也提及了, 自平衡 这个词说明了每次在我们进行增删时,会自行调整结构来满足红黑树特性,这样在查询上就能保证性能。
那么,什么样的二叉树才是红黑树呢?
1.节点是红色或黑色。 2.根是黑色。 3.所有叶子都是黑色(叶子是NIL节点)。 4.每个红色节点必须有两个黑色的子节点。(从每个叶子到根的所有路径上不能有两个连续的红色节点。) 5.从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。
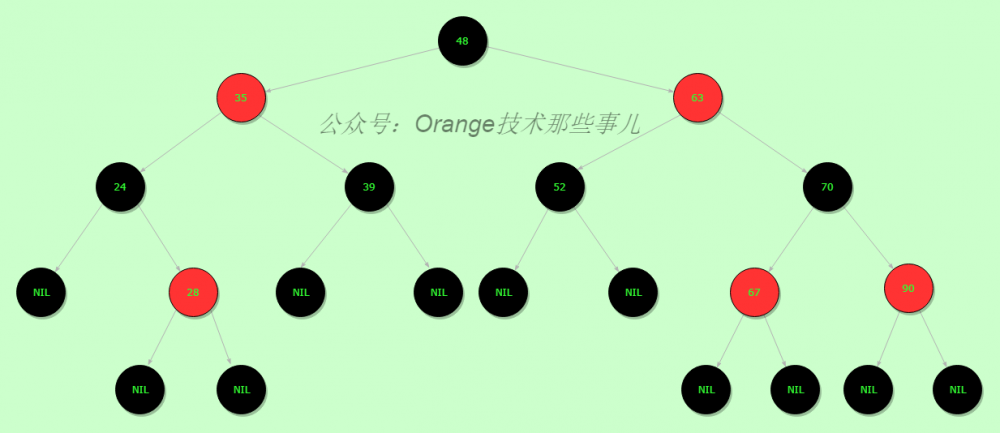
这里需要注意叶子节点的概念与一般意义上树的叶子节点不同,这里红黑树叶子节点都是黑色且为NIL的。
维基百科上对于这5种性质也做了说明:
这些约束确保了红黑树的关键特性:从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果是这个树大致上是平衡的。因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例,这个在高度上的理论上限允许红黑树在最坏情况下都是高效的,而不同于普通的二叉查找树。
要知道为什么这些性质确保了这个结果,注意到性质4导致了路径不能有两个毗连的红色节点就足够了。最短的可能路径都是黑色节点,最长的可能路径有交替的红色和黑色节点。因为根据性质5所有最长的路径都有相同数目的黑色节点,这就表明了没有路径能多于任何其他路径的两倍长。
在很多树数据结构的表示中,一个节点有可能只有一个子节点,而叶子节点包含数据。用这种范例表示红黑树是可能的,但是这会改变一些性质并使算法复杂。为此,本文中我们使用"nil叶子"或"空(null)叶子",如上图所示,它不包含数据而只充当树在此结束的指示。这些节点在绘图中经常被省略,导致了这些树好像同上述原则相矛盾,而实际上不是这样。与此有关的结论是所有节点都有两个子节点,尽管其中的一个或两个可能是空叶子。
从根到叶子的最长的可能路径不多于最短的可能路径的两倍长 这个在文中也解释了原因,因为性质4需要被满足,这样限制了树的高度差,使得查找性能提升。
可以多想下,普通的二叉树,最坏情况如下:
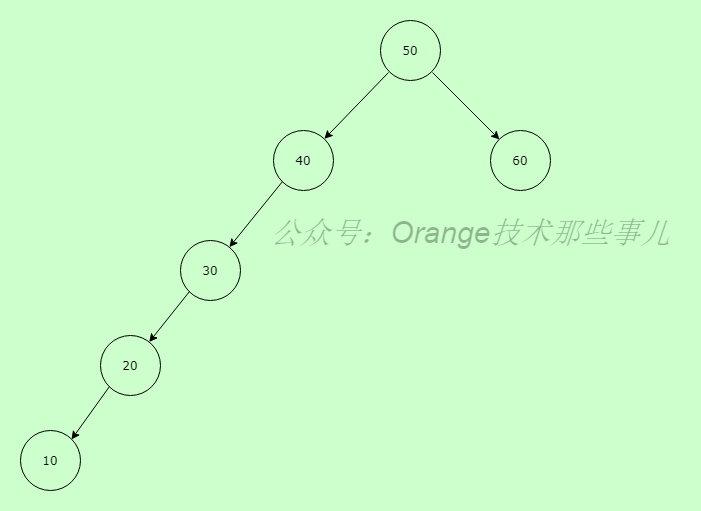
这种情况下使得树形结构毫无意义,而红黑树(其存在的5种特性保证)则不会出现这种情况。
树高度
具体请参考维基百科的证明:

自平衡操作
之前的定义我也说了,为了保证红黑树的特性,需要在插入删除时对树进行调整来保证自平衡。那么如何来调整呢?
这里就说明下红黑树平衡的两种操作: 变色和旋转 。
变色
变色这个操作很好理解了吧,在某些情况下,为了保证自平衡,需要改变颜色,来满足红黑树的特性
旋转
可以参考维基百科: https://en.wikipedia.org/wiki...
旋转操作相对要复杂些,旋转分为左旋和右旋。
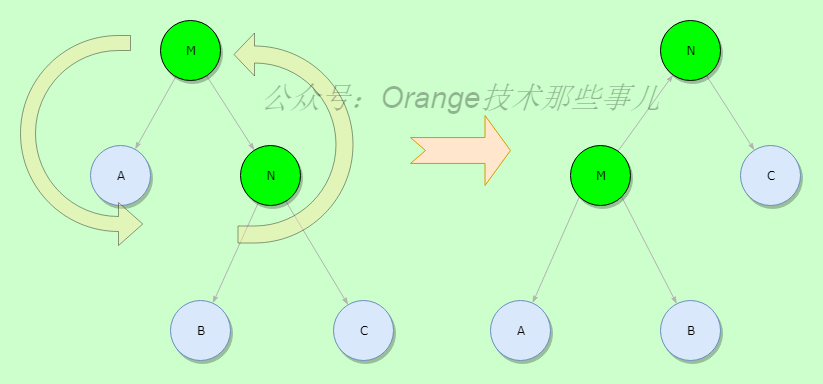
- 左旋:
如下图所示,逆时针旋转旋转M,N两个节点,使得父节点M变为N的子节点,N变为父节点,交换之后对于B节点就需要进行调整,B节点变为M的右子节点
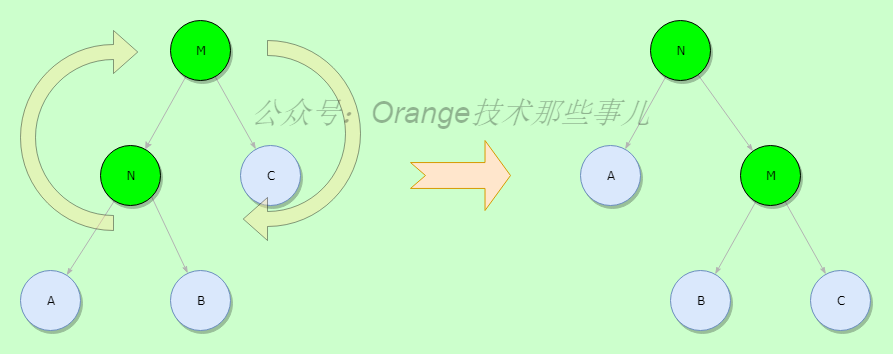
- 右旋:
如下图所示,顺时针旋转旋转M,N两个节点,使得父节点M变为N的子节点,N变为父节点,交换之后对于B节点就需要进行调整,B节点变为M的左子节点
这里贴出维基上的gif图,方便各位理解:

无论是变色还是旋转,最终调整的结果都是要在插入或者删除之后满足红黑树的5个特性。
插入调整
首先需要明白的是新增加的节点默认标记为 红色 ,至于原因维基上说明了:
如果设为黑色,就会导致根到叶子的路径上有一条路上,多一个额外的黑节点,这个是很难调整的。但是设为红色节点后,可能会导致出现两个连续红色节点的冲突,那么可以通过颜色调换(color flips)和树旋转来调整。
在说我个人理解之前,需要理解 局部红黑子树 含义,其实相当于把红黑树进行切割,一个大的红黑树切割成多个局部,每次我们调整都是以一个局部来完成,局部调整完之后,整个树如果还是不平衡,则继续向上回溯调整,维基上也是这样做的。下图中的框算是一个局部红黑子树。
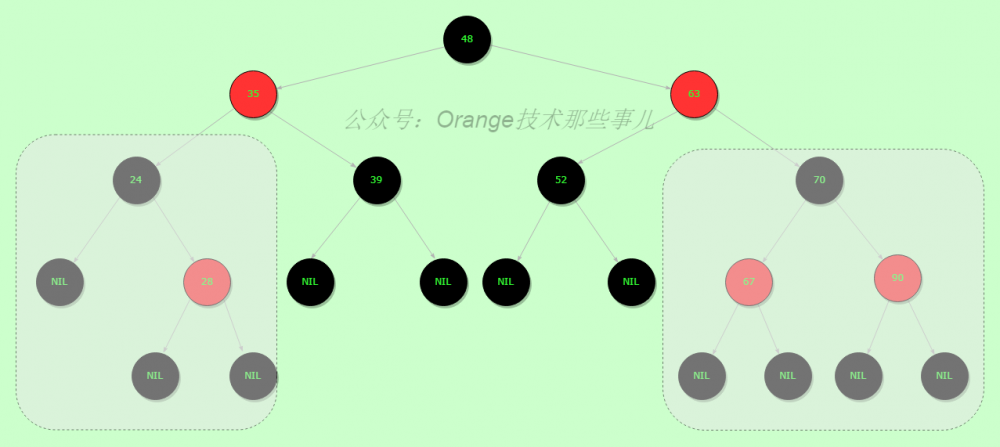
如果添加的节点默认标记为黑色,那么这条路径上比其他路径多了一个黑色节点,不满足性质5,需要调整,可能会影响到其他已经平衡的局部红黑子树,牵一发而动全身,代价过高,而默认为红色,首先其他已经平衡的局部红黑子树还未受到影响,在未调整之前,未平衡的这个局部红黑子树中黑色路径和平衡之前是相同的,这样应该是要更方便调整。
将要插入的节点标为N,N的父节点标为P,N的祖父节点标为G,N的叔父节点标为U
这里也能看出来都是以一个局部来调整,那么考虑下插入会出现哪些情况?在考虑的时候一定要注意,在未插入新节点和插入新节点之后变化的地方和需要保持不变的地方。尤其需要注意插入前已经平衡了,满足红黑树的5种特性,不是随便什么状态都会出现,切记。
1.N为根节点,即红黑树的根节点。 2.N的父节点(P)是黑色的。 3.N的父节点(P)是红色的(因此它不能是树的根)而N的叔父节点(U)是红色的。 4.N的父节点(P)是红色的(因此它不能是树的根)而N的叔父节点(U)是黑色的。
思考下,上面包含的情况可以从插入节点N为红色开始进行考虑,判断父节点颜色,根据情况进行调整,先进行变色操作,变色保证不了平衡则需要旋转来平衡,而3和4的情况,有人可能会想为什么要判断U侧的子树部分?我们可以想一下,在P为红色,N为红色时,在N这一侧的子树部分,如何调整也不会达到平衡,此时只能向上回溯寻求帮助,涉及到了祖父节点G,那么此时就会影响到G的子树U部分,所以需要考虑U的颜色然后继续调整。
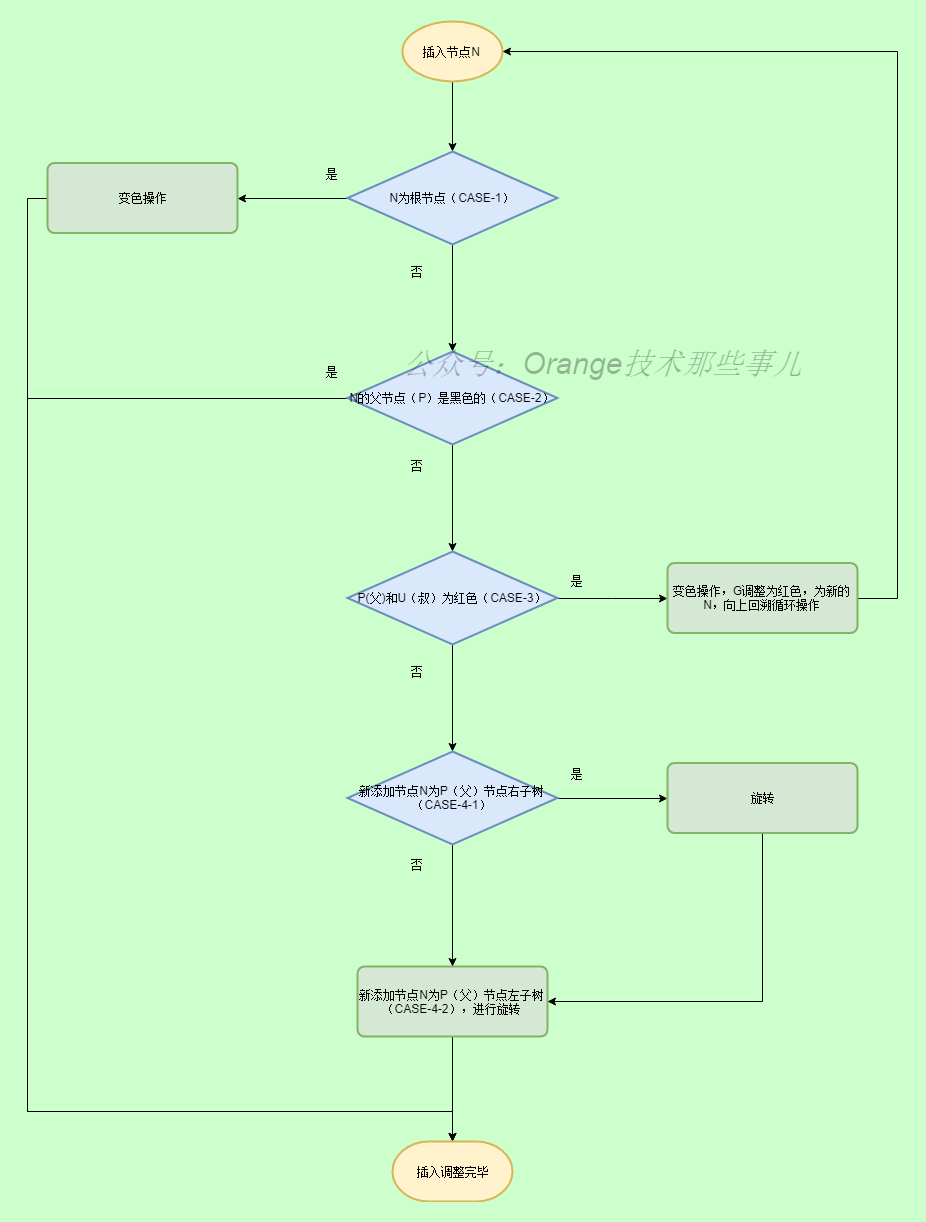
插入时按顺序判断上述4种情况,注意先对局部红黑子树(从N到G,G相当于局部根节点)进行平衡,满足属性4和5,最后判断G节点是否为黑色,非黑色以G为新增节点再次递归顺序判断(相当于向上回溯),这里有一个要注意的地方,局部根节点G可以为红色,除非G是整个树的根节点,这时直接修改颜色即可完成平衡(相当于整个树黑色路径都加一):
CASE-1:N为根节点,修改成黑色,同样满足红黑树的5个属性,仅仅黑色路径增加了1。不满足当前情况,继续CASE-2情况判断处理。
CASE-2:P为黑色,添加节点N为红色,N下添加两个黑色叶子节点(NIL),属性4和5没有破坏,不需要调整。不满足当前情况,继续CASE-3情况判断处理。
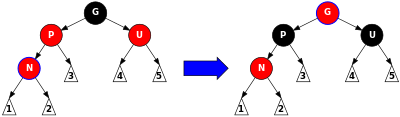
CASE-3:P(父)和U(叔)为红色,以N为P的左子节点为例(右子节点操作类似),添加节点N为红色,先进行变色操作,P,U变为黑色,这样不满足属性5,路径上黑色节点多了1,将G(祖父)变为红色,到这里可以看出添加节点之后从G到G下的叶子节点路径和未添加N节点之前的路径黑色节点数是一致的,在这部分局部区域已经满足属性4和5,不需要进行调整了,但是G可能违反了属性2(根节点为黑色),或属性4(不能有连续的两个红色节点),回到CASE-1再次顺序判断处理,这里注意下,重新判断是以G节点为新局部红黑子树的新增节点N,G节点的子节点可以当做叶子节点,再重新重头判断这个新的局部子树(相当于向上回溯,直到满足条件,或者根节点,满足CASE-1)。不满足当前情况,继续CASE-4情况判断处理。
CASE-4:P(父)为红色,U(叔)为黑色,以P为其父节点左子节点为例,对称情况操作类似,变色也满足不了G到叶子节点属性4和属性5,这里就需要考虑另一种处理-旋转。
这里会出现两种状态(对称的情况自行参照处理):
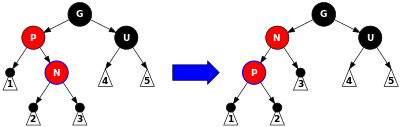
CASE-4-1:新添加节点N为P(父)节点右子树,相当于G树的“内部”,参考下图,在这种情况下,执行的P上的左旋转。转换成右侧图,到此还是违反属性4,但是不违反属性5,再继续CASE-4-2情况判断处理。不满足当前情况,也继续CASE-4-2情况判断处理。
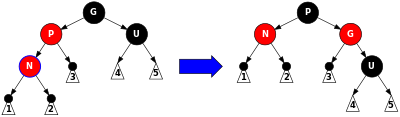
CASE-4-2:新添加节点N为P(父)节点左子树,相当于G树的“外部”,和第一种状态调整完一致,参考下图,在这种情况下,执行G上的右旋转,P和G的颜色切换,即可满足红黑树的属性,变为右侧图。
从上面分析过程可以看出,局部插入最多两次旋转,更多的是变色操作,少量的旋转操作可以锁住某些节点(变色操作不影响),大部分节点是可以查询且修改的,这也是大部分底层实现使用红黑树的原因吧。
总结
删除操作比较复杂,下一章再进行说明,本章主要从基础说明红黑树的特性以及相关的平衡操作以及插入新节点时不同情况的调整规则,希望对读者有所帮助,下面通过流程图来帮助各位更好的理解和实现红黑树插入情况下的自平衡处理。
下一章我就更为复杂的删除操作进行讲解,谢谢各位阅读,如有错误,欢迎留言指正,我将尽快验证修改。
参考资料:
- https://zh.wikipedia.org/wiki...
- https://en.wikipedia.org/wiki...










![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)

