树结构与Java实现
树结构与Java实现

目录
前言
提到『树』这种数据结构,相信很多人首先想到的就是『二叉树』。
的确,二叉树作为一种重要的数据结构,它结合了数组和链表的优点,有很多重要的应用。
我们都知道,数组的特点是查询迅速,根据index可以快速定位到一个元素。但是,如果要插入一个元素,就需要将这个元素位置之后的所有元素后移。平均来讲,一个长度为N的有序数组,插入元素要移动的元素个数为N/2。有序数组的插入的时间复杂度为O(N),删除操作的时间复杂度也为O(N)。
对于插入和删除操作频繁的数据,不建议采用有序数组。
链表的插入和删除效率都很高,只要改变一些值的引用就行了,时间复杂度为O(1)。但是链表的查询效率很低,每次都要从头开始找,依次访问链表的每个数据项。平均来说,要从一个有N个元素的链表查询一个元素,要遍历N/2个元素,时间复杂度为O(N)
对于查找频繁的数据,不建议使用链表。
本节先不介绍二叉树,而是先讲一下树这种数据结构。相信有了本节的知识作为基础,再了解二叉树就会轻松很多。
树的概念
概述
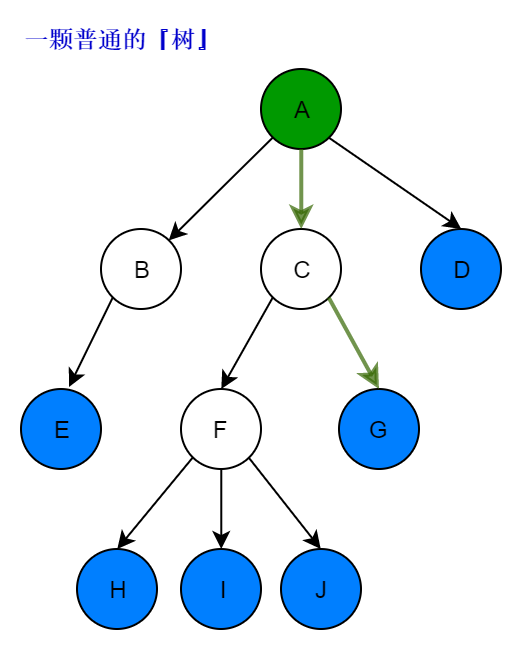
在计算机科学中,树(英语:tree)是一种抽象数据类型(ADT)或是实现这种抽象数据类型的数据结构,用来模拟具有树状结构性质的数据集合。
它是由n(n>0)个有限节点组成一个具有层次关系的集合。
把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
它具有以下的特点:
每个节点都只有有限个子节点或无子节点; 没有父节点的节点称为根节点; 每一个非根节点有且只有一个父节点; 除了根节点外,每个子节点可以分为多个不相交的子树; 树里面没有环路(cycle) —— 维基百科
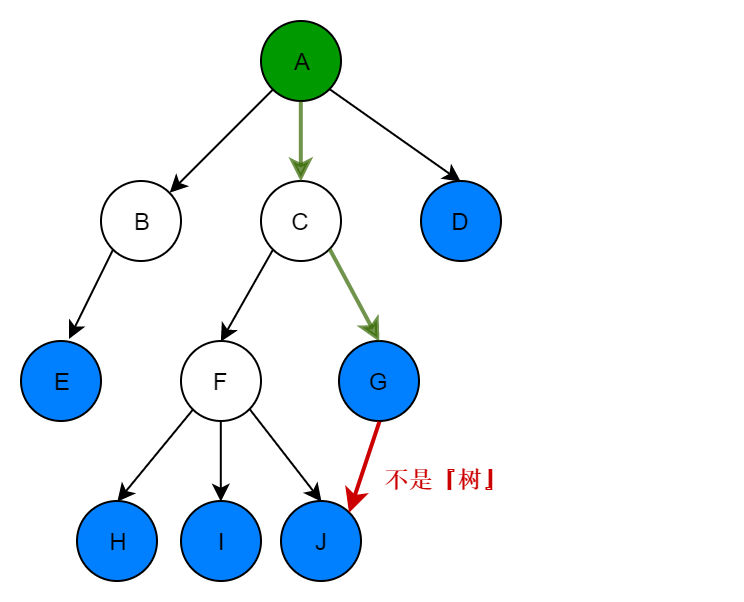
根据树的定义,下面的结构就不是『树』:
术语
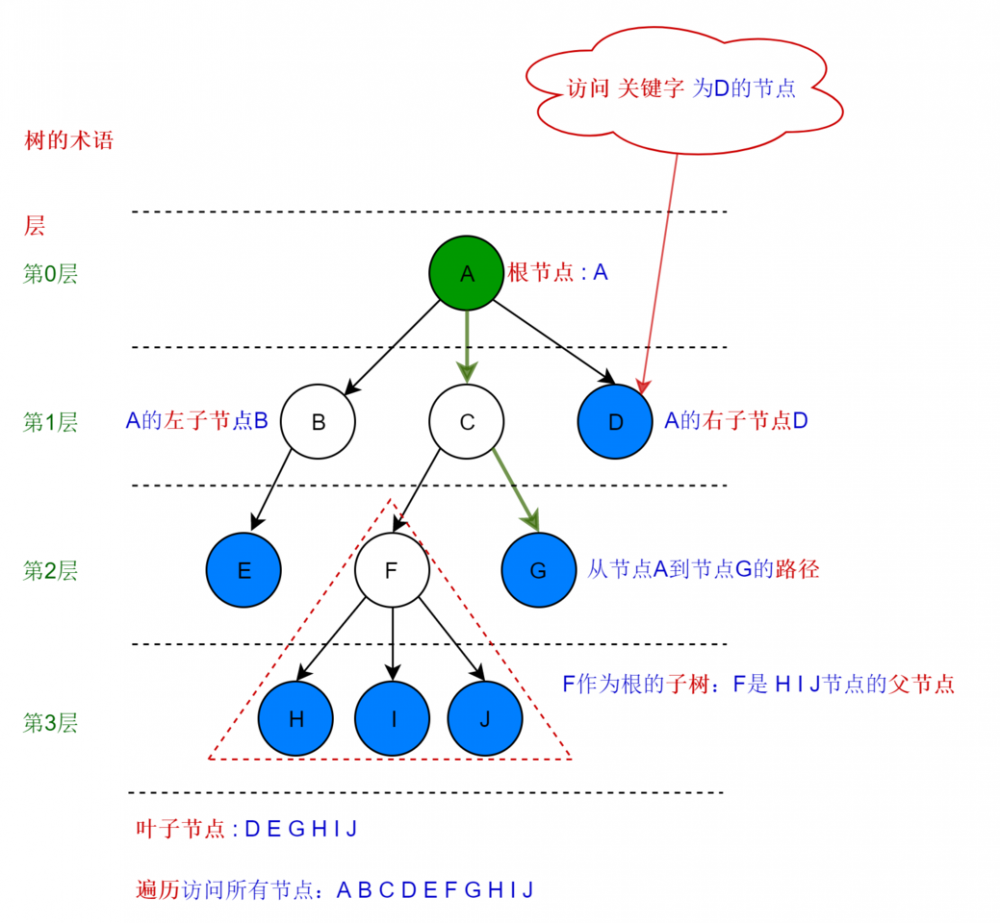
- 路径
从某个节点依次到达另外一个节点所经过的所有节点,就是这两个节点之间的路径。
- 根
树顶端的节点被称为根。从根出发到达任意一个节点只有一条路径。
- 父节点
除了根节点之外,每个节点都可以向上找到一个唯一的节点,这个节点就是当前节点的父节点。相应的,父节点下方的就是子节点。
- 叶子节点
没有子节点的“光杆司令”就被称为叶子节点。
- 子树
每个子节点作为根节点的树都是一个子树。
- 层
一个树结构的代数就是这个树的层。
- 度
一棵树中,最大的节点的度称为树的度。
- 兄弟节点
具有相同父节点的节点互称为兄弟节点;
实际应用
树结构有非常广泛的应用,比如我们常用的文件目录系统,就是一个树结构。
例如在Windows10操作系统的CMD命令行输入 tree 命令,就可以输出目录树:
tree
卷 Windows 的文件夹 PATH 列表
卷序列号为 1CEB-7ABE
C:.
├─blog
│ ├─cache
│ │ └─JavaCacheGuidance
│ ├─datastructure
│ ├─editor
│ │ └─notepad++
│ ├─framework
│ │ └─guava
│ │ └─retry
│ ├─git
│ └─java
│ └─package-info
├─category
│ ├─food
│ │ ├─fruit
│ │ └─self
│ ├─job
│ │ └─bz
│ │ └─project
│ │ └─ad
│ │ └─exch
│ ├─people
│ ├─practical
│ │ └─work
│ │ └─ecommerce
│ │ └─inventory
│ ├─tech
│ │ ├─algorithm
│ │ │ └─tree
│ │ └─java
│ │ ├─concurrent
│ │ │ └─thread
│ │ ├─design
│ │ ├─i18n
│ │ ├─jcf
│ │ └─spring
│ │ └─springboot
│ └─tool
│ ├─data
│ │ └─db
│ │ ├─mysql
│ │ └─redis
│ └─site
│ └─stackoverflow
└─me
└─phonephoto
复制代码
实现树
讲解了树结构的特点和相关概念以后,下面用Java实现树结构的基本操作,并演示创建树、添加子节点、遍历树和搜索指定节点等操作。
TreeNode
package net.ijiangtao.tech.algorithms.algorithmall.datastructure.tree;
import java.util.Iterator;
import java.util.LinkedList;
import java.util.List;
/**
* 实现树结构
*
* @author ijiangtao
* @create 2019-04-18 15:13
**/
public class TreeNode<T> implements Iterable<TreeNode<T>> {
/**
* 树节点
*/
public T data;
/**
* 父节点,根没有父节点
*/
public TreeNode<T> parent;
/**
* 子节点,叶子节点没有子节点
*/
public List<TreeNode<T>> children;
/**
* 保存了当前节点及其所有子节点,方便查询
*/
private List<TreeNode<T>> elementsIndex;
/**
* 构造函数
*
* @param data
*/
public TreeNode(T data) {
this.data = data;
this.children = new LinkedList<TreeNode<T>>();
this.elementsIndex = new LinkedList<TreeNode<T>>();
this.elementsIndex.add(this);
}
/**
* 判断是否为根:根没有父节点
*
* @return
*/
public boolean isRoot() {
return parent == null;
}
/**
* 判断是否为叶子节点:子节点没有子节点
*
* @return
*/
public boolean isLeaf() {
return children.size() == 0;
}
/**
* 添加一个子节点
*
* @param child
* @return
*/
public TreeNode<T> addChild(T child) {
TreeNode<T> childNode = new TreeNode<T>(child);
childNode.parent = this;
this.children.add(childNode);
this.registerChildForSearch(childNode);
return childNode;
}
/**
* 获取当前节点的层
*
* @return
*/
public int getLevel() {
if (this.isRoot()) {
return 0;
} else {
return parent.getLevel() + 1;
}
}
/**
* 递归为当前节点以及当前节点的所有父节点增加新的节点
*
* @param node
*/
private void registerChildForSearch(TreeNode<T> node) {
elementsIndex.add(node);
if (parent != null) {
parent.registerChildForSearch(node);
}
}
/**
* 从当前节点及其所有子节点中搜索某节点
*
* @param cmp
* @return
*/
public TreeNode<T> findTreeNode(Comparable<T> cmp) {
for (TreeNode<T> element : this.elementsIndex) {
T elData = element.data;
if (cmp.compareTo(elData) == 0)
return element;
}
return null;
}
/**
* 获取当前节点的迭代器
*
* @return
*/
@Override
public Iterator<TreeNode<T>> iterator() {
TreeNodeIterator<T> iterator = new TreeNodeIterator<T>(this);
return iterator;
}
@Override
public String toString() {
return data != null ? data.toString() : "[tree data null]";
}
}
复制代码
TreeNodeIterator
package net.ijiangtao.tech.algorithms.algorithmall.datastructure.tree;
import java.util.Iterator;
/**
*
* 迭代器
*
* @author ijiangtao
* @create 2019-04-18 15:24
**/
public class TreeNodeIterator<T> implements Iterator<TreeNode<T>> {
enum ProcessStages {
ProcessParent, ProcessChildCurNode, ProcessChildSubNode
}
private ProcessStages doNext;
private TreeNode<T> next;
private Iterator<TreeNode<T>> childrenCurNodeIter;
private Iterator<TreeNode<T>> childrenSubNodeIter;
private TreeNode<T> treeNode;
public TreeNodeIterator(TreeNode<T> treeNode) {
this.treeNode = treeNode;
this.doNext = ProcessStages.ProcessParent;
this.childrenCurNodeIter = treeNode.children.iterator();
}
@Override
public boolean hasNext() {
if (this.doNext == ProcessStages.ProcessParent) {
this.next = this.treeNode;
this.doNext = ProcessStages.ProcessChildCurNode;
return true;
}
if (this.doNext == ProcessStages.ProcessChildCurNode) {
if (childrenCurNodeIter.hasNext()) {
TreeNode<T> childDirect = childrenCurNodeIter.next();
childrenSubNodeIter = childDirect.iterator();
this.doNext = ProcessStages.ProcessChildSubNode;
return hasNext();
} else {
this.doNext = null;
return false;
}
}
if (this.doNext == ProcessStages.ProcessChildSubNode) {
if (childrenSubNodeIter.hasNext()) {
this.next = childrenSubNodeIter.next();
return true;
} else {
this.next = null;
this.doNext = ProcessStages.ProcessChildCurNode;
return hasNext();
}
}
return false;
}
@Override
public TreeNode<T> next() {
return this.next;
}
/**
* 目前不支持删除节点
*/
@Override
public void remove() {
throw new UnsupportedOperationException();
}
}
复制代码
测试
下面实现的树结构,与前面图中的树结构完全相同。
package net.ijiangtao.tech.algorithms.algorithmall.datastructure.tree;
/**
* tree
*
* @author ijiangtao
* @create 2019-04-18 15:03
**/
public class TreeDemo1 {
public static void main(String[] args) {
System.out.println("********************测试遍历*************************");
TreeNode<String> treeRoot = getSetA();
for (TreeNode<String> node : treeRoot) {
String indent = createIndent(node.getLevel());
System.out.println(indent + node.data);
}
System.out.println("********************测试搜索*************************");
Comparable<String> searchFCriteria = new Comparable<String>() {
@Override
public int compareTo(String treeData) {
if (treeData == null)
return 1;
boolean nodeOk = treeData.contains("F");
return nodeOk ? 0 : 1;
}
};
TreeNode<String> foundF = treeRoot.findTreeNode(searchFCriteria);
System.out.println("F: parent=" + foundF.parent + ",children=" + foundF.children);
}
private static String createIndent(int depth) {
StringBuilder sb = new StringBuilder();
for (int i = 0; i < depth; i++) {
sb.append(' ');
}
return sb.toString();
}
public static TreeNode<String> getSetA() {
TreeNode<String> A = new TreeNode<String>("A");
{
TreeNode<String> B = A.addChild("B");
TreeNode<String> C = A.addChild("C");
TreeNode<String> D = A.addChild("D");
{
TreeNode<String> E = B.addChild("E");
TreeNode<String> F = C.addChild("F");
TreeNode<String> G = C.addChild("G");
{
TreeNode<String> H = F.addChild("H");
TreeNode<String> I = F.addChild("I");
TreeNode<String> J = F.addChild("J");
}
}
}
return A;
}
}
复制代码
- 输出
********************测试遍历************************* A B E C F H I J G D ********************测试搜索************************* F: parent=C,children=[H, I, J] 复制代码
总结
本节我带领大家一起了解了树这种重要的数据结构,并且讲解了树相关的概念和术语,最后为大家实现了基本的树操作。
学习完本节内容,对我们下面要介绍的二叉树,以及Java中 TreeSet 和 TreeMap 的源码,都会有所帮助。











![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)

