转载

AVL树的Java实现

定义

Wikipedia - AVL树

在计算机科学中，AVL树是最早被发明的自平衡二叉查找树。在AVL树中，任一节点对应的两棵子树的最大高度差为1，因此它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下的时间复杂度都是 {displaystyle O(log {n})} O(log{n})。增加和删除元素的操作则可能需要借由一次或多次树旋转，以实现树的重新平衡。AVL树得名于它的发明者G. M. Adelson-Velsky和Evgenii Landis，他们在1962年的论文《An algorithm for the organization of information》中公开了这一数据结构。

理论

实现AVL树的要点为：每次新增/删除节点后 判断平衡性 然后通过 调整 使整棵树重新平衡

判断平衡性：每次新增/删除节点后，刷新受到影响的节点的高度，即可通过任一节点的左右子树高度差判断其平衡性

调整：通过对部分节点的父子关系的改变使树重新平衡

实现

基本结构 

public class Tree<T extends Comparable<T>> {

    private static final int MAX_HEIGHT_DIFFERENCE = 1;

    private Node<T> root;

    class Node<KT> {

        KT key;

        Node<KT> left;

        Node<KT> right;

        int height = 1;

        public Node(KT key, Node<KT> left, Node<KT> right) {
            this.key = key;
            this.left = left;
            this.right = right;
        }
    }
}

插入（insert）

四种不平衡范型

对于任意一次 插入所造成的 不平衡，都可以简化为下述四种范型之一：

下面四张图中的数字仅代表节点序号，为了后文方便展示调整过程

4、5、6、7号节点代表了四棵高度可以使不平衡成立的子树（遵循插入的规则）

  • LL型

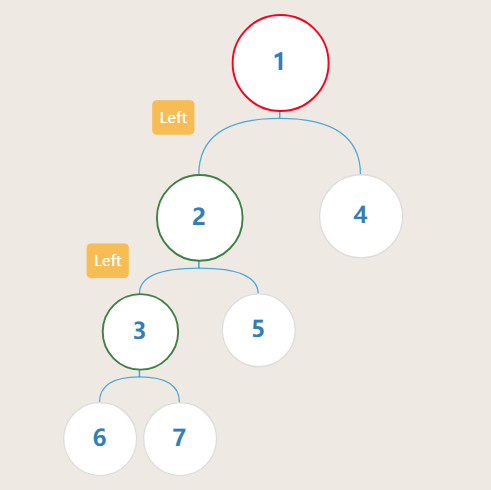
AVL树的Java实现

  • LR型

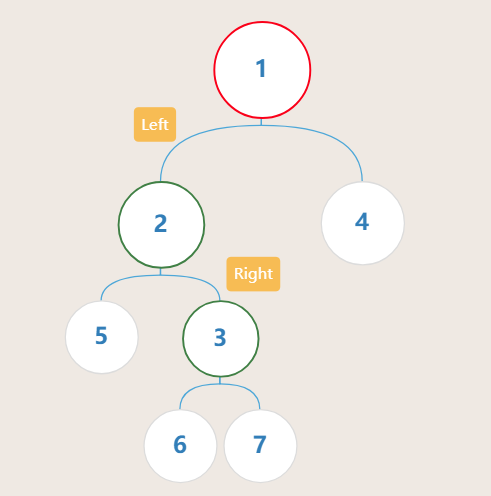
AVL树的Java实现

  • RR型

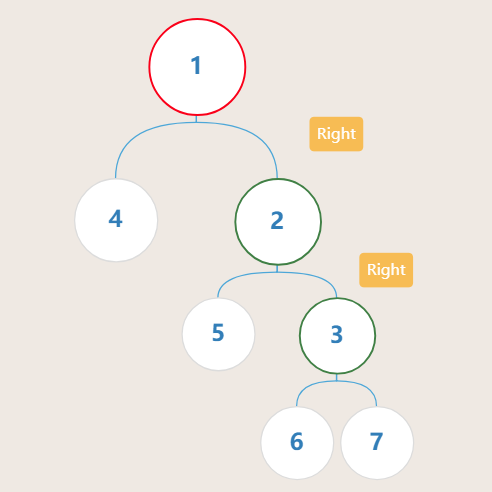
AVL树的Java实现

  • RL型

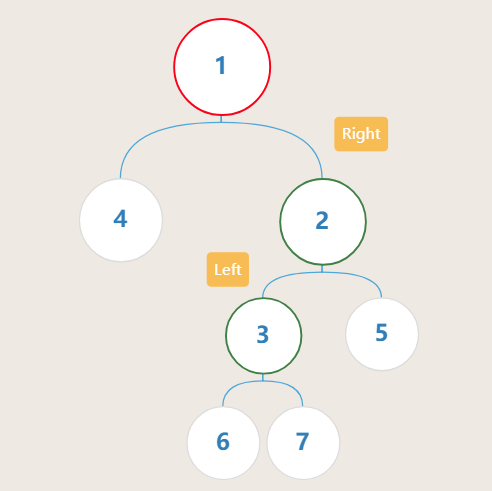
AVL树的Java实现

总结得到判断范型的方法为：不平衡的节点（节点1）通往高度最大的子树的叶子节点时所途经的前两个节点（节点2、节点3）的方向

调整方法

  • LL型

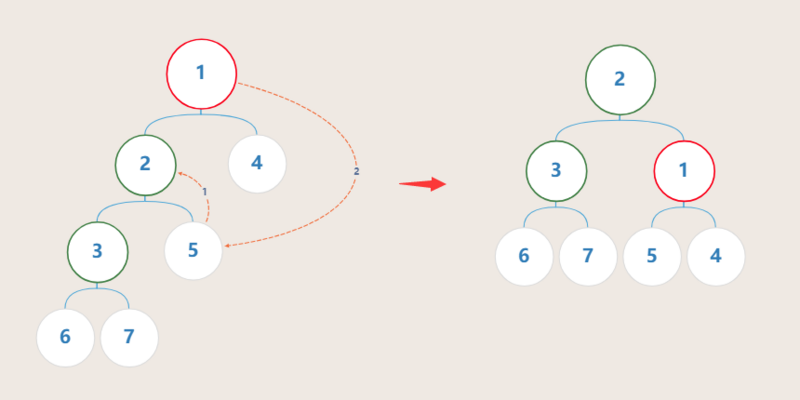
AVL树的Java实现

  1. 5号节点 作为 1号节点 的左孩子
  2. 1号节点 作为 2号节点 的右孩子

例子（例子中的数字代表节点的值）：

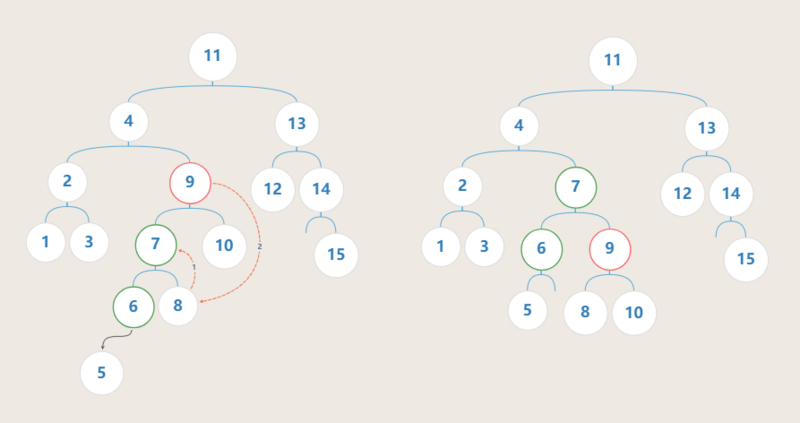
AVL树的Java实现

插入 节点5 后造成 节点9 不平衡，其范型为 LL型 ，按照固定步骤调整后全局重新达到平衡

  • LR型

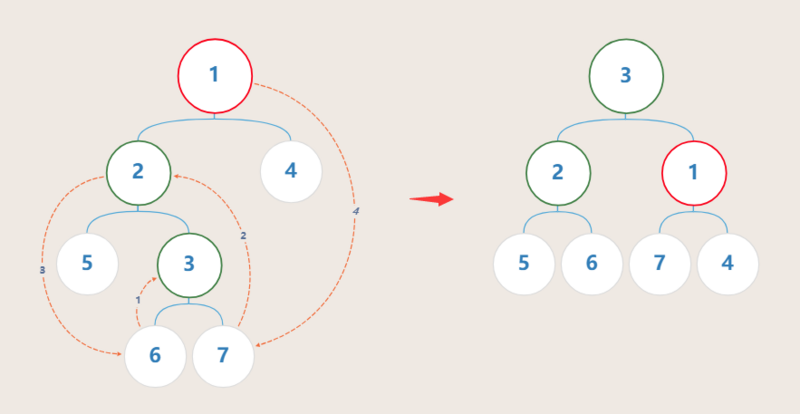
AVL树的Java实现

  1. 6号节点 作为 2号节点 的右孩子
  2. 7号节点 作为 1号节点 的左孩子
  3. 2号节点 作为 3号节点 的左孩子
  4. 1号节点 作为 3号节点 的右孩子

例子（例子中的数字代表节点的值）：

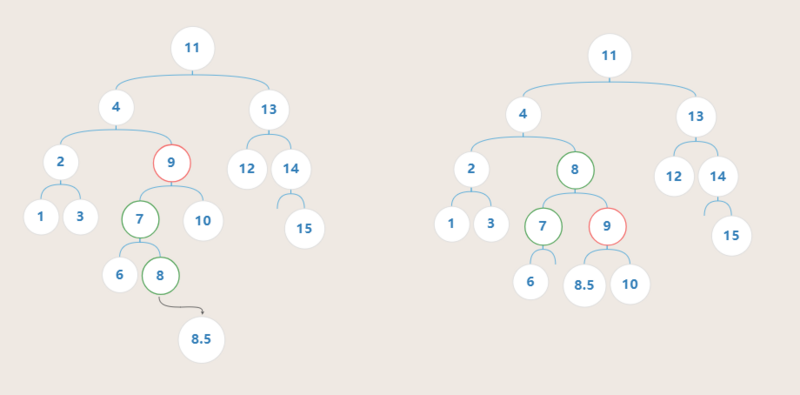
AVL树的Java实现

插入 节点8.5 后造成 节点9 不平衡，其范型为 LR型 ，按照固定步骤调整后全局重新达到平衡

  • RR型

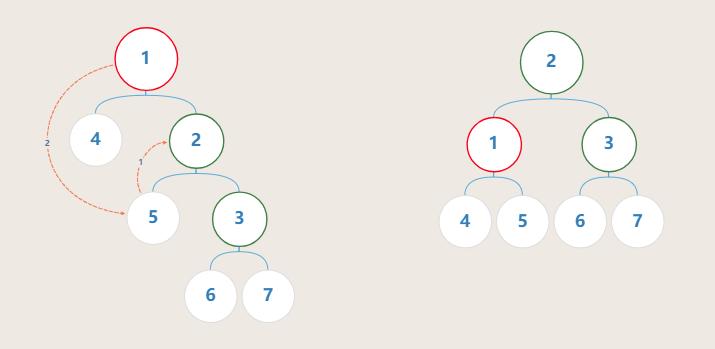
AVL树的Java实现

  1. 5号节点 作为 1号节点 的右孩子
  2. 1号节点 作为 2号节点 的左孩子

例子（例子中的数字代表节点的值）：

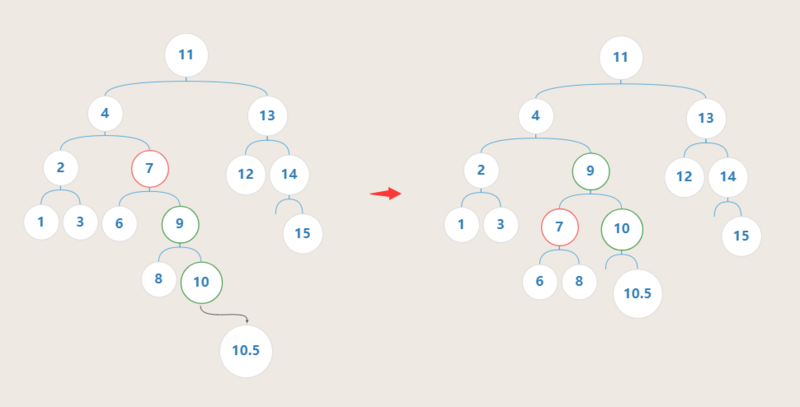
AVL树的Java实现

插入 节点10.5 后造成 节点7 不平衡，其范型为 RR型 ，按照固定步骤调整后全局重新达到平衡

  • RL型

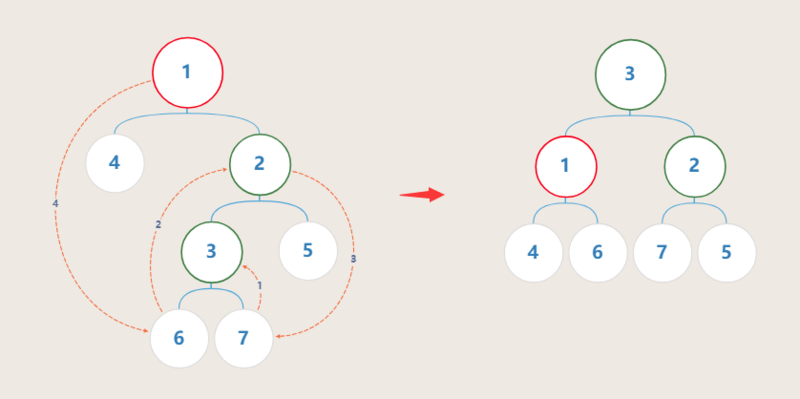
AVL树的Java实现

  1. 7号节点 作为 2号节点 的左孩子
  2. 6号节点 作为 1号节点 的右孩子
  3. 2号节点 作为 3号节点 的右孩子
  4. 1号节点 作为 3号节点 的左孩子

例子（例子中的数字代表节点的值）：

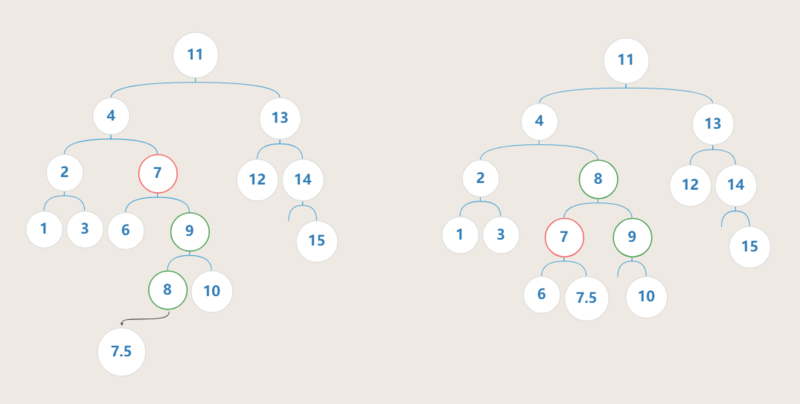
AVL树的Java实现

插入 节点7.5 后造成 节点7 不平衡，其范型为 RL型 ，按照固定步骤调整后全局重新达到平衡

代码实现 

public void insert(T key) {
    if (key == null) {
        throw new NullPointerException();
    }
    root = insert(root, key);
}

private Node<T> insert(Node<T> node, T key) {
    if (node == null) {
        return new Node<>(key, null, null);
    }

    int cmp = key.compareTo(node.key);
    if (cmp == 0) {
        return node;
    }
    if (cmp < 0) {
        node.left = insert(node.left, key);
    } else {
        node.right = insert(node.right, key);
    }

    if (Math.abs(height(node.left) - height(node.right)) > MAX_HEIGHT_DIFFERENCE) {
        node = balance(node);
    }
    refreshHeight(node);
    return node;
}

private int height(Node<T> node) {
    if (node == null) {
        return 0;
    }
    return node.height;
}

private void refreshHeight(Node<T> node) {
    node.height = Math.max(height(node.left), height(node.right)) + 1;
}

/**
 * 此方法中的node, node1, node2分别代表上文范型中的1、2、3号节点
 */
private Node<T> balance(Node<T> node) {
    Node<T> node1, node2;
    // ll
    if (height(node.left) > height(node.right) &&
            height(node.left.left) > height(node.left.right)) {
        node1 = node.left;
        node.left = node1.right;
        node1.right = node;

        refreshHeight(node);
        return node1;
    }
    // lr
    if (height(node.left) > height(node.right) &&
            height(node.left.right) > height(node.left.left)) {
        node1 = node.left;
        node2 = node.left.right;
        node.left = node2.right;
        node1.right = node2.left;
        node2.left = node1;
        node2.right = node;

        refreshHeight(node);
        refreshHeight(node1);
        return node2;
    }
    // rr
    if (height(node.right) > height(node.left) &&
            height(node.right.right) > height(node.right.left)) {
        node1 = node.right;
        node.right = node1.left;
        node1.left = node;

        refreshHeight(node);
        return node1;
    }
    // rl
    if (height(node.right) > height(node.left) &&
            height(node.right.left) > height(node.right.right)) {
        node1 = node.right;
        node2 = node.right.left;
        node.right = node2.left;
        node1.left = node2.right;
        node2.left = node;
        node2.right = node1;

        refreshHeight(node);
        refreshHeight(node1);
        return node2;
    }
    return node;
}

总结

由插入节点导致的局部不平衡均会符合上述四种范型之一，只需要按照固定的方式调整相关节点的父子关系即可使树恢复平衡

关于调整，很多博客或者书籍中将这种调整父子关系的过程称为 旋转 ，这个就见仁见智了，个人觉得这种描述并不容易理解，故本文统一称为调整

删除（remove）

通常情况

对于删除节点这个操作来说，有两个要点： 被删除节点的空缺应该如何填补 以及 删除后如何使树恢复平衡

  • 被删除节点的空缺应该如何填补
  1. 如果被删除节点是叶子节点，则不需要填补空缺
  2. 而如果是枝干节点，则需要填补空缺，理想的情况是使用某个节点填补被删除节点的空缺后，整棵树仍然保持平衡
    a) 如果节点的左右子树有一棵为空，则使用 非空子树 填补空缺
    b) 如果节点的左右子树均为非空子树，则使用节点的左右子树中 更高 的那棵子树中的 最大/最小节点 来填补空缺（如果子树高度一致则哪边都可以）

例子：

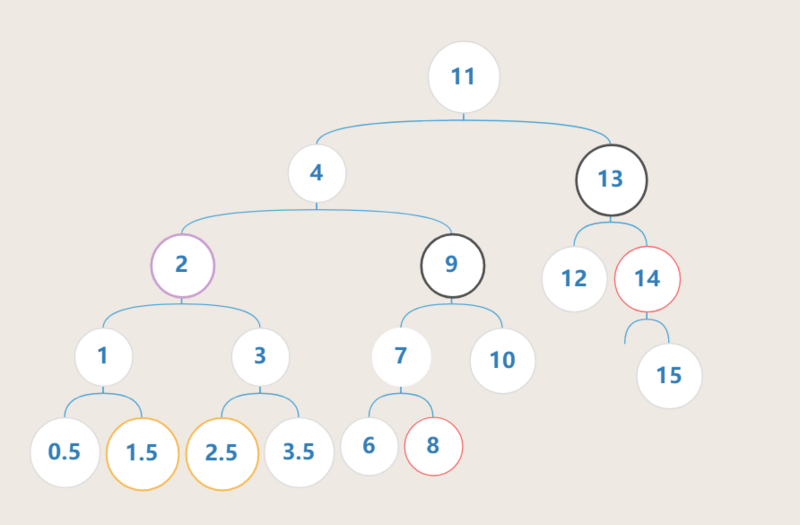
AVL树的Java实现

  1. 假设待删除节点为 节点9 ，则应当使用 左子树中的最大值 节点8 来填补空缺
  2. 假设待删除节点为 节点13 ，则应当使用 右子树中的最小值 节点14 来填补空缺
  3. 假设待删除节点为 节点2 ，则使用 左子树中的最大值 节点1.5 或者 右子树中的最小值 节点2.5 来填补空缺均可

按照上述方式来填补空缺，可以尽可能保证删除后整棵树仍然保持平衡

  • 删除后如何使树恢复平衡

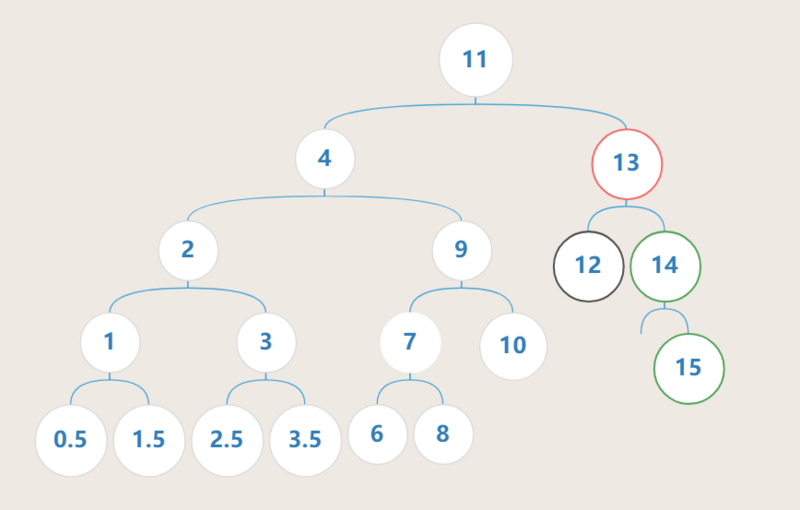
AVL树的Java实现

如图， 叶子节点12 为被删除节点，删除后不需要填补空缺，但是此时 节点13 产生了不平衡

不过 节点13 的不平衡满足上文所说的不平衡范型中的 RR型 ，因此只需要对 节点13 做对应的调整即可，如图：

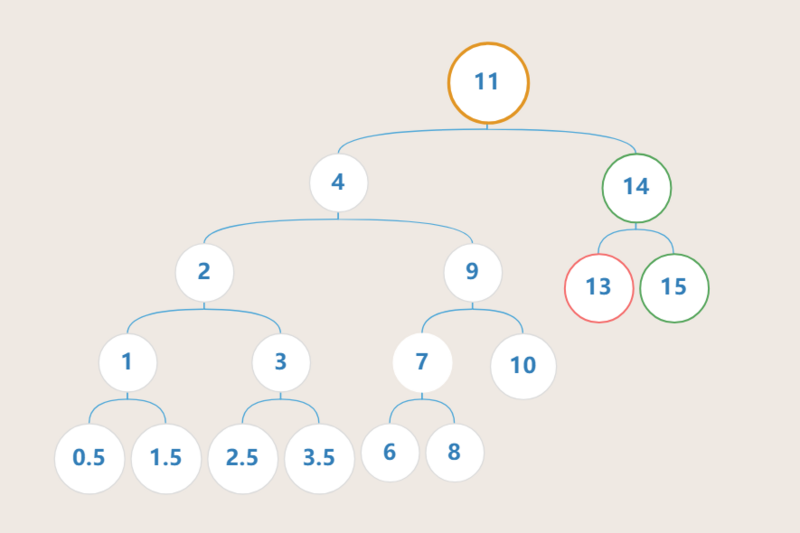
AVL树的Java实现

此时 节点13 所在的子树经过调整重新达到局部平衡

但是我们紧接着发现， 节点11 出现了不平衡，其左子树高度为4，右子树高度为2

如果此时按照插入情况下的不平衡范型判断方法去判断 节点11 的不平衡情况属于哪种范型，会发现无法满足四种范型的任一情况

特殊情况

由删除节点导致的不平衡，除了会出现插入中所说的四种范型之外，还会出现两种情况，如图：

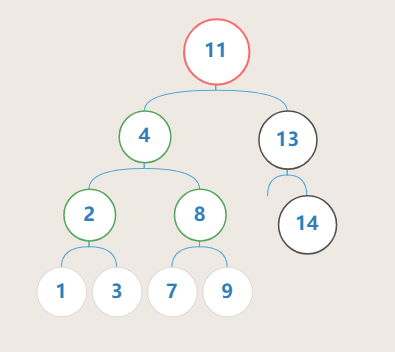
AVL树的Java实现

整棵树初始状态为平衡状态，此时假设删除 节点13 或 节点14 ，均会导致 节点11 产生不平衡（左子树高度3，右子树高度1）

但是如果仍然按照插入时的方法来判断不平衡，则会发现， 节点4 的左右子树高度一致，即在满足了 L 后，后续无法判断这种情况属于哪种范型

对于 R 方向也是一样

本文称它们为 L型 和 R型

不过这两种情况的处理也很简单，实际上当出现这种情况时，使用 LL型 或 LR型 的调整方法均可以达到使树重新平衡的目的

如图：

AVL树的Java实现

两种调整方式均可使树重新平衡，对于 R型 也是一样，这里不再赘述

代码实现 

public void remove(T key) {
    if (key == null) {
        throw new NullPointerException();
    }
    root = remove(root, key);
}

private Node<T> remove(Node<T> node, T key) {
    if (node == null) {
        return null;
    }

    int cmp = key.compareTo(node.key);
    if (cmp < 0) {
        node.left = remove(node.left, key);
    }
    if (cmp > 0){
        node.right = remove(node.right, key);
    }
    if (cmp == 0) {
        if (node.left == null || node.right == null) {
            return node.left == null ? node.right : node.left;
        }
        var successorKey = successorOf(node).key;
        node = remove(node, successorKey);
        node.key = successorKey;
    }

    if (Math.abs(height(node.left) - height(node.right)) > MAX_HEIGHT_DIFFERENCE) {
        node = balance(node);
    }
    refreshHeight(node);
    return node;
}

/**
 * 寻找被删除节点的继承者
 */
private Node<T> successorOf(Node<T> node) {
    if (node == null) {
        throw new NullPointerException();
    }
    if (node.left == null || node.right == null) {
        return node.left == null ? node.right : node.left;
    }

    return height(node.left) > height(node.right) ?
            findMax(node.left, node.left.right, node.left.right == null) :
            findMin(node.right, node.right.left, node.right.left == null);
}

private Node<T> findMax(Node<T> node, Node<T> right, boolean rightIsNull) {
    if (rightIsNull) {
        return node;
    }
    return findMax((node = right), node.right, node.right == null);
}

private Node<T> findMin(Node<T> node, Node<T> left, boolean leftIsNull) {
    if (leftIsNull) {
        return node;
    }
    return findMin((node = left), node.left, node.left == null);
}

其中用到的 private Node<T> balance(Node<T> node) 方法修改为： 

private Node<T> balance(Node<T> node) {
    Node<T> node1, node2;
    // ll & l
    if (height(node.left) > height(node.right) &&
            height(node.left.left) >= height(node.left.right)) {
        node1 = node.left;
        node.left = node1.right;
        node1.right = node;

        refreshHeight(node);
        return node1;
    }
    // lr
    if (height(node.left) > height(node.right) &&
            height(node.left.right) > height(node.left.left)) {
        node1 = node.left;
        node2 = node.left.right;
        node.left = node2.right;
        node1.right = node2.left;
        node2.left = node1;
        node2.right = node;

        refreshHeight(node);
        refreshHeight(node1);
        return node2;
    }
    // rr & r
    if (height(node.right) > height(node.left) &&
            height(node.right.right) >= height(node.right.left)) {
        node1 = node.right;
        node.right = node1.left;
        node1.left = node;

        refreshHeight(node);
        return node1;
    }
    // rl
    if (height(node.right) > height(node.left) &&
            height(node.right.left) > height(node.right.right)) {
        node1 = node.right;
        node2 = node.right.left;
        node.right = node2.left;
        node1.left = node2.right;
        node2.left = node;
        node2.right = node1;

        refreshHeight(node);
        refreshHeight(node1);
        return node2;
    }
    return node;
}

也就是将 L型 情况包含进了 LL型 ， R型 的情况包含进了 RR型 ，因为这两种范式的调整要比对应的 LR型 / RL型 的操作数少

总结

尽管删除节点时会出现特殊的情况，但是仍然可以通过简单的调整使树始终保持平衡

完整代码 

/**
 * AVL-Tree
 *
 * @author Shinobu
 * @since 2019/5/7
 */
public class Tree<T extends Comparable<T>> {

    private static final int MAX_HEIGHT_DIFFERENCE = 1;

    private Node<T> root;

    class Node<KT> {

        KT key;

        Node<KT> left;

        Node<KT> right;

        int height = 1;

        public Node(KT key, Node<KT> left, Node<KT> right) {
            this.key = key;
            this.left = left;
            this.right = right;
        }
    }

    public Tree(T... keys) {
        if (keys == null || keys.length < 1) {
            throw new NullPointerException();
        }

        root = new Node<>(keys[0], null, null);
        for (int i = 1; i < keys.length && keys[i] != null; i++) {
            root = insert(root, keys[i]);
        }
    }

    public T find(T key) {
        if (key == null || root == null) {
            return null;
        }
        return find(root, key, key.compareTo(root.key));
    }

    private T find(Node<T> node, T key, int cmp) {
        if (node == null) {
            return null;
        }

        if (cmp == 0) {
            return node.key;
        }

        return find(
                (node = cmp > 0 ? node.right : node.left),
                key,
                node == null ? 0 : key.compareTo(node.key));
    }

    public void insert(T key) {
        if (key == null) {
            throw new NullPointerException();
        }
        root = insert(root, key);
    }

    private Node<T> insert(Node<T> node, T key) {
        if (node == null) {
            return new Node<>(key, null, null);
        }

        int cmp = key.compareTo(node.key);
        if (cmp == 0) {
            return node;
        }
        if (cmp < 0) {
            node.left = insert(node.left, key);
        } else {
            node.right = insert(node.right, key);
        }

        if (Math.abs(height(node.left) - height(node.right)) > MAX_HEIGHT_DIFFERENCE) {
            node = balance(node);
        }
        refreshHeight(node);
        return node;
    }

    private int height(Node<T> node) {
        if (node == null) {
            return 0;
        }
        return node.height;
    }

    private void refreshHeight(Node<T> node) {
        node.height = Math.max(height(node.left), height(node.right)) + 1;
    }

    private Node<T> balance(Node<T> node) {
        Node<T> node1, node2;
        // ll & l
        if (height(node.left) > height(node.right) &&
                height(node.left.left) >= height(node.left.right)) {
            node1 = node.left;
            node.left = node1.right;
            node1.right = node;

            refreshHeight(node);
            return node1;
        }
        // lr
        if (height(node.left) > height(node.right) &&
                height(node.left.right) > height(node.left.left)) {
            node1 = node.left;
            node2 = node.left.right;
            node.left = node2.right;
            node1.right = node2.left;
            node2.left = node1;
            node2.right = node;

            refreshHeight(node);
            refreshHeight(node1);
            return node2;
        }
        // rr & r
        if (height(node.right) > height(node.left) &&
                height(node.right.right) >= height(node.right.left)) {
            node1 = node.right;
            node.right = node1.left;
            node1.left = node;

            refreshHeight(node);
            return node1;
        }
        // rl
        if (height(node.right) > height(node.left) &&
                height(node.right.left) > height(node.right.right)) {
            node1 = node.right;
            node2 = node.right.left;
            node.right = node2.left;
            node1.left = node2.right;
            node2.left = node;
            node2.right = node1;

            refreshHeight(node);
            refreshHeight(node1);
            return node2;
        }
        return node;
    }

    public void remove(T key) {
        if (key == null) {
            throw new NullPointerException();
        }
        root = remove(root, key);
    }

    private Node<T> remove(Node<T> node, T key) {
        if (node == null) {
            return null;
        }

        int cmp = key.compareTo(node.key);
        if (cmp < 0) {
            node.left = remove(node.left, key);
        }
        if (cmp > 0){
            node.right = remove(node.right, key);
        }
        if (cmp == 0) {
            if (node.left == null || node.right == null) {
                return node.left == null ? node.right : node.left;
            }
            var successorKey = successorOf(node).key;
            node = remove(node, successorKey);
            node.key = successorKey;
        }

        if (Math.abs(height(node.left) - height(node.right)) > MAX_HEIGHT_DIFFERENCE) {
            node = balance(node);
        }
        refreshHeight(node);
        return node;
    }
    
    private Node<T> successorOf(Node<T> node) {
        if (node == null) {
            throw new NullPointerException();
        }
        if (node.left == null || node.right == null) {
            return node.left == null ? node.right : node.left;
        }

        return height(node.left) > height(node.right) ?
                findMax(node.left, node.left.right, node.left.right == null) :
                findMin(node.right, node.right.left, node.right.left == null);
    }

    private Node<T> findMax(Node<T> node, Node<T> right, boolean rightIsNull) {
        if (rightIsNull) {
            return node;
        }
        return findMax((node = right), node.right, node.right == null);
    }

    private Node<T> findMin(Node<T> node, Node<T> left, boolean leftIsNull) {
        if (leftIsNull) {
            return node;
        }
        return findMin((node = left), node.left, node.left == null);
    }

}

结语

AVL树的实现，在了解了不平衡的六种情况，以及对应的处理方式后，还是比较简单且逻辑清晰的

本文实现的AVL树的增删查三种操作，全部基于递归的算法模式，考虑到在树足够大时递归的效率问题，本人尝试进行了一些尾递归优化，希望这能使操作效率更高一些

后续

也许

会学习并尝试实现一下红黑树，然后对比一下二者的效率

文章如果有谬误或疏漏，还请务必指正，感谢万分

原文  https://segmentfault.com/a/1190000019101902
正文到此结束
所属分类： Java 编程技术

热门推荐

相关文章

阿里云首购8折
说给你听

本文目录
随机标签
书籍教程
springboot-demo Java入门教程 bootstrap3 CSS Apache基础教程 php ionic 教程 Python mysql教程 eclipse Ubuntu VPS系统配置 AngularJS 教程 MongoDB教程 Struts2教程 Redis教程 Spring教程 Git教程 Jenkins进阶系列 openfire参考指南 Java设计模式 HBase教程 Maven教程 hibernate教程 Docker 教程 memcached教程 Quartz指南 springcloud-demo Hive教程 Ant教程 ANTLR教程 SpringCloud java实例教程 XStream教程 Hazelcast教程 Elastic-Job-Lite 深入浅出MyBatis SVN教程 ibaties教程 rabittmq教程 solr教程 Hadoop教程 WebService CXF学习 JPA教程 ActiveMQ中文指南 java-demo Java内存模型 dubbo教程 python3-demo Linux入门视频教程
近期评论
  1. 1 如何将Spring Cloud Task发布Data Flow上执行？
  2. 2 Spring Cloud Data Flow快速入门Demo
  3. 3 Spring Cloud Consul实现选举机制
  4. 4 Spring Boot集成ShedLock实现分布式定时任务
  5. 5 利用oss进行数据库和网站图片备份
  6. 6 Spring Cloud Stream实现数据流处理
  7. 7 Python3访问MySQL数据库快速入门Demo
  8. 8 Github开源项目作者可以免费申请 JetBrains 全家桶
  9. 9 Spring Cloud Vault快速入门Demo
  10. 10 Spring Cloud Gateway快速入门Demo
网站信息
  • 文章总数：82,716 篇
  • 文件总数：284,297 个
  • 标签总数：2,396 个
  • 分类总数：85 个
  • 留言数量：2,560 条
  • 在线人数：605 人
  • 运行天数：4,411天
  • 最后更新：2024年11月24日09点
Loading...

其他链接

关于本站

本站定位：个人技术类博客

本站作用：写博客、记日志、闲聊扯淡鼓捣技术。

问题交流

[HBLOG]公众号 HBLOG HBLOG