转载

Java random方法的安全问题

前言

起源于强网杯的密码学题目random study

java.util.Random

题目中challenge two的主要代码如下：

o = subprocess.check_output(["java", "Main"])
tmp=[]
for i in o.split("/n")[0:3]:
    tmp.append(int(i.strip()))
v1=tmp[0] % 0xffffffff
v2=tmp[1] % 0xffffffff
v3=tmp[2] % 0xffffffff

还给了一个Main.class文件，打开发现是字节码，用jd-gui反编译得到源码如下：

public class Main {
  public static void main(String[] paramArrayOfString) {
    Random random = new Random();
    System.out.println(random.nextInt());
    System.out.println(random.nextInt());
    System.out.println(random.nextInt());
  }
}

代码的意思很简单，调用random.nextInt方法生成三个连续的随机数，要求根据前两个随机数去预测第三个随机数

源码分析

为了了解这个方法出现的安全问题的原理，有必要去查看一下这个方法的源代码

在eclipse中将光标移动到nextInt处按F3可以追踪到jdk包里的具体代码

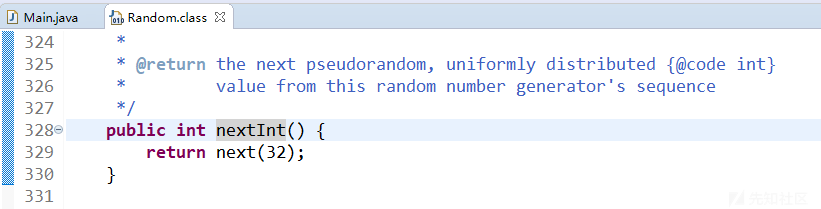
Java random方法的安全问题

可以看到它直接调用了next方法，传递的参数是32。

继续追踪next方法

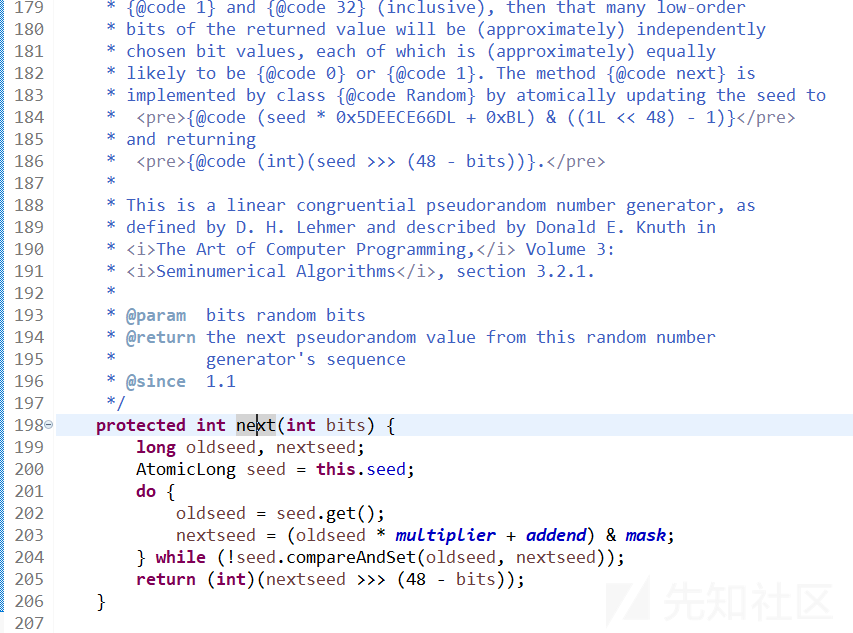
Java random方法的安全问题

可以看到前一个随机数种子和后一个随机数种子都是定义为long类型的，方法返回的值就是下一个种子右移 16位然后强转为 int 的结果

while里的compareAndSet方法只是比较当前的种子值是否为oldseed，如果是的话就更新为nextseed而已，一般都会返回true

而下一个种子的更新算法就在do-while循环里面： nextseed = (oldseed * multiplier + addend) & mask ，种子的初始值是将当前系统时间带入运算的结果

可以在类定义的开头处看到这几个常量属性的值

Java random方法的安全问题

而这个种子的更新算法本质上就是一个线性同余生成器

线性同余生成器（LCG）

LCG是形如这样的式子：

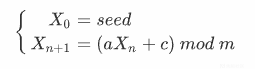
Java random方法的安全问题

和上面的代码对比可以看出是基本一致的，因为和mask常量做与运算就相当于是舍弃高位，保留2进制的低47位，也就相当于模2的48次方

那么我们既然都有了常量的值了，我们就可以去做第三个随机数的预测了

预测

方法很简单，如果把生成第一个随机数的种子定义为seed1，seed2、seed3往后顺延的话

seed1 右移 16位就是第一个随机数的值，也就是说第一个随机数就丢失了16位，所以seed1就有2的16次方种可能，那么把这2的16次方种可能带入计算下一个seed2，并且右移查看是否和第二个随机数相等就能知道是否正确找到了seed1了

先看一组简单的测试样例，输出的三个随机数都是正数

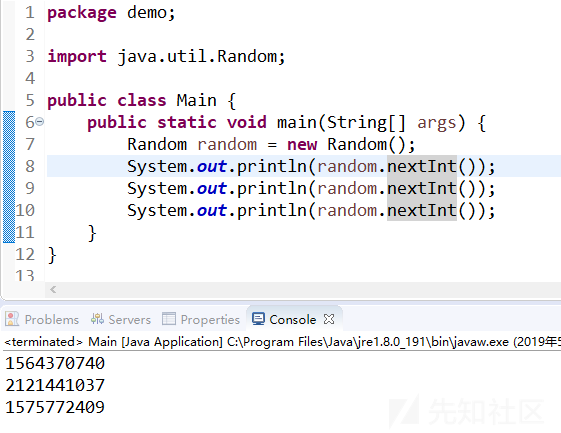
Java random方法的安全问题

a = 0x5DEECE66DL
b = 0xBL
mask = (1L << 48) - 1

def findseed(x1, x2):
    seed = x1 << 16
    for i in range(2 ** 16):
        if ((a * seed + b) & mask) >> 16 == x2:
            return  seed
        seed += 1

if __name__ == '__main__':
    x1 = 1564370740
    x2 = 2121441037

    seed1 = findseed(x1, x2)
    seed2 = (a * seed1 + b) & mask
    x3 = ((a * seed2 + b) & mask) >> 16
    print x3

通过测试，结果正确

但是你可能会好奇为什么测试的java代码有时候会输出负数，因为右移1位是相当于除以2的，一个正数除以一个正数怎么会得到一个负数呢？

实际上这是由于java代码中的int强制类型转换和>>>无符号右移所造成的

补码

先来回顾一下java的int类型，int类型占四个字节，也就是二进制的32位

计算机中的数字通常用二进制补码表示，最高位为符号位，正数为0，负数为1，所以表示数值的一共有31位，故int类型的最小值为-2147483648（-2的31次方）最大值为 2147483647（2的31次方-1）

你可能会好奇为什么负数比正数多表示了1位，因为自然数0就是用全为0（包括符号位）的二进制表示的，而到负数那里是没有负0的概念的，所以可以多表示一个数

接下来可以开始说>>>的意思了

java中有两种右移，一种是>>，代表逻辑上的右移(除以)，高位补为符号位；一种是>>>代表无符号右移，高位直接补0

看一下这种情况：

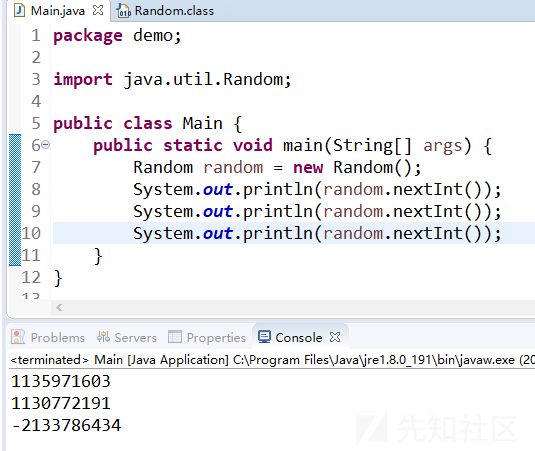
Java random方法的安全问题

前两个为正数，但是第三个为负数，我们先按照上面的方法计算出seed3和它右移16位的结果：

a = 0x5DEECE66DL
b = 0xBL
mask = (1L << 48) - 1

def findseed(x1, x2):
    seed = x1 << 16
    for i in range(2 ** 16):
        if ((a * seed + b) & mask) >> 16 == x2:
            return  seed
        seed += 1

if __name__ == '__main__':
    x1 = 1135971603
    x2 = 1130772191

    seed1 = findseed(x1, x2)
    seed2 = (a * seed1 + b) & mask
    seed3 = (a * seed2 + b) & mask
    print seed3
    print seed3.bit_length()
    print '{:064b}'.format(seed3)
    print '{:064b}'.format(seed3>>16)

输出结果为

这样就能看出问题在哪了，由于seed3右移了16位以后除了补0的高位就只有32位了，使用int强转以后java把它从long类型转换成了int，并且自动忽略了32位以后的高位，这就相当于我们得到的第三个随机数用补码表示为 10000000110100010000000010111110

可以看出来最高位为1，也就是说这个补码代表了一个负数，那么我们怎么通过补码找到这个负数的真值呢？很简单，对补码再求一次补码就行了，也就是取反后加1。

即 01111111001011101111111101000010 ，对应的二进制为2133786434，所以第三个随机数应该为-2133786434，如此一来，我们就可以通过负数找到其对应的seed了

exp

最终通过两个随机数预测第三个随机数的exp如下：

a = 0x5DEECE66DL
b = 0xBL
mask = (1L << 48) - 1

def n2p(x):
    y = -x
    y ^= 2 ** 32 - 1 #取反
    y += 1
    return y

def findseed(x1, x2):
    if x1 < 0:
        x1 = n2p(x1)

    if x2 < 0:
        x2 = n2p(x2)

    seed = x1 << 16
    for i in range(2 ** 16):
        if ((a * seed + b) & mask) >> 16 == x2:
            return seed
        seed += 1

def cal_x(seed):
    x = seed>>16
    if '{:032b}'.format(x).startswith('1'):
        x ^= 2 ** 32 - 1
        x += 1
        return -x
    return x

if __name__ == '__main__':
    x1 = 187562908
    x2 = 1663125607

    seed1 = findseed(x1, x2)
    seed2 = (a * seed1 + b) & mask
    seed3 = (a * seed2 + b) & mask
    x3 = cal_x(seed3)
    print x3

经过测试，无论x1或者x2是否为负数，都可以准确预测