位图数据结构及其在-Java和-Redis中的应用
什么是位图?BitMap,大家直译为位图. 我的理解是:位图是内存中连续的二进制位(bit),可以用作对大量整形做去重和统计.
引入一个小栗子来帮助理解一下:
假如我们要存储三个int数字 (1,3,5) ,在java中我们用一个int数组来存储,那么占用了12个字节.但是我们申请一个bit数组的话.并且把相应下标的位置为1,也是可以表示相同的含义的,比如
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| 二进制值 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
可以看到,对应于 1,3,5 为下标的bit上的值为1,我们或者计算机也是可以get到 1,3,5 这个信息的.
优势
那么这么做有什么好处呢?感觉更麻烦了鸭,下面这种存储方式,在申请了 bit[8] 的场景下才占用了一个字节,占用内存是原来的12分之一,当数据量是海量的时候,比如40亿个int,这时候节省的就是10几个G的内存了.
这就引入了位图的第一个优势,占用内存小.
再想一下,加入我们现在有一个位图,保存了用户今天的签到数据.下标可以是用户的ID.
A:
| 用户ID | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| 二进制值 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
这代表了用户(1,3,5)今天签到了.
当然还有昨天的位图,
B:
| 用户ID | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| 二进制值 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
这代表了用户(1,2,3,7)昨天签到了.
我们现在想求:
- 昨天和今天都签到的用户.
- 昨天或者今天签到的用户.
在关系型数据库中存储的话,这将是一个比较麻烦的操作,要么要写一些表意不明的SQL语句,要么进行两次查询,然后在内存中双重循环去判断.
而使用位图就很简单了, A & B , A | B 即可.上面的操作明显是一个集合的 与或 操作,而二进制天然就支持逻辑操作,且
众所周知猫是液体
.错了,众多周知是计算机进行二进制运算的效率很高.
这就是位图的第二个优点:支持与或运算且效率高.
哇,这么完美,
那么哪里可以买到呢?
,那么有什么缺点呢?
不足
当然有,位图不能很方便的支持 非运算 ,(当然,关系型数据库支持的也不好).这句话可能有点难理解.继续举个例子:
我们想查询今天没有签到的用户,直接对位图进行取非是不可以的.
对今天签到的位图取非得到的结果如下:
| 用户ID | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| 二进制值 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
这意味着今天(0,2,4,6,7)用户没有签到吗?不是的,存在没有7(任意数字)号用户的情况,或者他注销了呢.
这是因为位图只能表示布尔信息,即 true/false .他在这个位图中,表示的是 XX用户今天有签到或者没有签到 ,但是不能额外的表达, xx用户存在/不存在这个状态 了.
但是我们可以曲线救国,首先搞一个全集用户的位图.比如:
全集:
| 用户ID | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| 二进制值 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 |
然后用全集的位图和签到的位图做异或操作,相同则为0,不相同则为1.
在业务的逻辑为: 用户存在和是否签到两个bool值,共四种组合.
- 用户存在,且签到了. 两个集合的对应位都为1,那么结果就为0.
- 用户存在,但是没签到. 全集对应位为1,签到为0,所以结果是1.
- 用户不存在,那么必然没可能签到, 两个集合的对应位都是0,结果为0.
所以结果中,为1的只有一种可能: 用户存在且没有签到 ,正好是我们所求的结果.
A ^ 全集:
| 用户ID | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| 二进制值 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
此外,位图对于稀疏数据的表现不是很好,(当然聪明的大佬们已经基本解决掉了这个问题).原生的位图来讲,如果我们只有两个用户,1号和100000000号用户,那么直接存储int需要8个字节也就是32个bit,而用位图存储需要1亿个bit.当数据 量少,且跨度极大 也就是稀疏的时候,原生的位图不太适合.
点击这里跳转到 稀疏数据 的解决方案
总结
那么我们来做一下总结:
位图是用二进制位来存储整形数据的一种数据结构,在很多方面都有应用,尤其是在大数据量的场景下,节省内存及提高运算效率十分实用.
他的优点有:
- 节省内存.-> 因此在大数据量的时候更加显著.
- 与或运算效率高.->可以快速求交集和并集.
缺点有:
- 不能直接进行非运算.-> 根本原因是位图只能存储一个布尔信息,信息多了就需要借助全量集合等数据辅助.
- 数据稀疏时浪费空间.-> 这个不用很担心,后面会讲到大佬们的解法,基本可以解决掉.
- 只能存储布尔类型.-> 有限制,但是业务中很多数据都可以转换为布尔类型.比如上面的例子中, 业务原意 :用户每天的签到记录,以用户为维度. 我们可以转换为 : 每天的每个用户是否签到,就变为了布尔类型的数据.
Java中的位图
上面讲了位图的原理,那么我们先来自己手动实现一个!
简陋版本
说明:因为后面还有JDK版本,所以这里只实现了很简陋的版本,方便理解位图的核心原理即可.这个简陋版本 完全不可以 直接使用,能跑,但是在很多情况下都会直接报错.
虽然简陋,但是必须的还是要有.
构造方法
写了一个仅支持bit数量的构造参数. 因为我们是用int数组来保存实际的数据,所以对传入的值 右移5 (相当于除以32,因为int是32位的嘛)就是int数组的大小.
set方法
支持将某一个位设置为true/false.
为了实现 set-true ,其实是有粗暴的符合人类思路的逻辑的,比如当调用 set(5,true) 的时候,我们将int数字转化为二进制字符串,得到 000000000000000000000000000000 (应该是32个我没数),然后将其右边第六位置为1,得到 000000000000000000000000100000 ,然后再转回int数字.
这个方法很符合 位图 的直接定义,也很好理解,但是对于计算机来说,太麻烦了,而且过程中需要一个String,占用太多的内存空间了.
计算机更喜欢使用或运算来解决. 假设现有数字为3,即 000000000000000000000000001000 ,这时候我们调用了 set(10,true) ,怎么办呢,首先使用左移,将第11位置为1,然后与原来的值进行或操作.像下面这样子:
原来值 : 000000000000000000000000001000 1右移10位: 000000000000000000010000000000 或操作的结果: 000000000000000000010000001000 ----> 可以直接表示 3 和 10 两个位上都为1了. 复制代码
设置某一个位为false,和上面的流程不太一样.除去粗暴的办法之外,还可以 对 1右移x位 的 非 取 与 .很拗口,下面是示例:
我们将3上的设为0.
原来值 : 000000000000000000010000001000 ----> 10和3上为1, 1右移3位: 000000000000000000000000001000 1右移3位取非后: 111111111111111111111111110111 原来的值与取非后取与: 000000000000000000010000000000 ----> 只有10上为1了. 复制代码
get方法
获取某个位上的值.
当然也可以用粗暴的转换二进制字符串解决,但是使用 与操作 更加快速且计算机友好.
对set方法中的例子来说,设置了3和10之后,如果获取10上的值,可以:
当前值: 000000000000000000010000001000 1右移10位: 000000000000000000010000000000 与操作的结果: 000000000000000000010000000000 ---> 只要这个数字不等于0,即说明10上为1,等于0则为0. 复制代码
实际的代码加注释如下:
/**
* Created by pfliu on 2019/07/02.
*/
public class BitMapTest {
// 实际使用int数组存储
private int[] data;
/**
* 构造方法,传入预期的最大index.
*/
public BitMapTest(int size) {
this.data = new int[size >> 5];
}
/**
* get 方法, 传入要获取的index, 返回bool值代表该位上为1/0
*/
public boolean get(int bitIdx) {
return (data[bitIdxToWorkIdx(bitIdx)] & (1 << bitIdx)) != 0;
}
/**
* 将对应位置的值设置为传入的bool值
*/
public void set(int idx, boolean v) {
if (v) {
set(idx);
} else {
clear(idx);
}
}
// 将index的值设置为1
private void set(int idx) {
data[bitIdxToWorkIdx(idx)] |= 1 << idx;
}
// 将index上的值设置为0
private void clear(int bitIdx) {
data[bitIdxToWorkIdx(bitIdx)] &= ~(1L << bitIdx);
}
// 根据bit的index获取它存储的实际int在数组中的index
private int bitIdxToWorkIdx(int bitIdx) {
return bitIdx >> 5;
}
public static void main(String[] args) {
BitMapTest t = new BitMapTest(100);
t.set(10, true);
System.out.println(t.get(9));
System.out.println(t.get(10));
}
}
复制代码
JDK版本(BitSet源码阅读)
JDK中对位图是有实现的,实现类为 BitSet ,其中大致思想和上面实现的简陋版本类似,只是其内部数据是使用long数组来存储,此外加了许多的容错处理.下面看一下源码.还是按照方法分类来看.
常量及变量
// long数组,64位的long是2的6次方
private final static int ADDRESS_BITS_PER_WORD = 6;
// 每一个word的bit数量
private final static int BITS_PER_WORD = 1 << ADDRESS_BITS_PER_WORD;
// 存储数据的long数组
private long[] words;
// 上面的数组中使用到了的word的个数
private transient int wordsInUse = 0;
// 数组的大小是否由用户指定的(注释里写明了:如果是true,我们假设用户知道他自己在干什么)
private transient boolean sizeIsSticky = false;
复制代码
构造方法及工厂方法
BitSet提供了两个公开的构造方法以及四个公开的工厂方法,分别支持从 long[] , LongBuffer , bytes [] , ByteBuffer 中获取BitSet实例.
各个方法及其内部调用的方法如下:
// ---------构造方法-------
// 无参的构造方法,初始化数组为长度为64个bit(即一个long)以及设置sizeIsSticky为false.
public BitSet() {
initWords(BITS_PER_WORD);
sizeIsSticky = false;
}
// 根据用户传入的bit数量进行初始化,且设置sizeIsSticky为true.
public BitSet(int nbits) {
// nbits can't be negative; size 0 is OK
if (nbits < 0)
throw new NegativeArraySizeException("nbits < 0: " + nbits);
initWords(nbits);
sizeIsSticky = true;
}
// ---------构造方法的调用链 -------
// 初始化数组
private void initWords(int nbits) {
words = new long[wordIndex(nbits-1) + 1];
}
// 根据bit数量获取long数组的大小,右移6位即可.
private static int wordIndex(int bitIndex) {
return bitIndex >> ADDRESS_BITS_PER_WORD;
}
// ---------工厂方法,返回BitSet实例 -------
// 传入long数组
public static BitSet valueOf(long[] longs) {
int n;
for (n = longs.length; n > 0 && longs[n - 1] == 0; n--)
;
return new BitSet(Arrays.copyOf(longs, n));
}
// 传入LongBuffer
public static BitSet valueOf(LongBuffer lb) {
lb = lb.slice();
int n;
for (n = lb.remaining(); n > 0 && lb.get(n - 1) == 0; n--)
;
long[] words = new long[n];
lb.get(words);
return new BitSet(words);
}
// 传入字节数组
public static BitSet valueOf(byte[] bytes) {
return BitSet.valueOf(ByteBuffer.wrap(bytes));
}
// 传入ByteBuffer
public static BitSet valueOf(ByteBuffer bb) {
bb = bb.slice().order(ByteOrder.LITTLE_ENDIAN);
int n;
for (n = bb.remaining(); n > 0 && bb.get(n - 1) == 0; n--)
;
long[] words = new long[(n + 7) / 8];
bb.limit(n);
int i = 0;
while (bb.remaining() >= 8)
words[i++] = bb.getLong();
for (int remaining = bb.remaining(), j = 0; j < remaining; j++)
words[i] |= (bb.get() & 0xffL) << (8 * j);
return new BitSet(words);
}
复制代码
set方法
BitSet提供了两类set方法,
- 单点set. 将某个index设置为tue/false.
- 范围set. 将某个范围值设置为tue/false.
因此BitSet有四个重载的set方法.
// 将某个index的值设置为true. 使用和上面自己实现的简陋版本相同的或操作.
public void set(int bitIndex) {
if (bitIndex < 0)
throw new IndexOutOfBoundsException("bitIndex < 0: " + bitIndex);
int wordIndex = wordIndex(bitIndex);
expandTo(wordIndex);
words[wordIndex] |= (1L << bitIndex); // Restores invariants
checkInvariants();
}
// 将某个index设置为传入的值,注意当传入值为false的时候,调用的是clear方法.
public void set(int bitIndex, boolean value) {
if (value)
set(bitIndex);
else
clear(bitIndex);
}
// 将index上bit置为0
public void clear(int bitIndex) {
if (bitIndex < 0)
throw new IndexOutOfBoundsException("bitIndex < 0: " + bitIndex);
int wordIndex = wordIndex(bitIndex);
if (wordIndex >= wordsInUse)
return;
words[wordIndex] &= ~(1L << bitIndex);
recalculateWordsInUse();
checkInvariants();
}
// 将from->to之间的所有值设置为true
public void set(int fromIndex, int toIndex) {
checkRange(fromIndex, toIndex);
if (fromIndex == toIndex)
return;
// Increase capacity if necessary
int startWordIndex = wordIndex(fromIndex);
int endWordIndex = wordIndex(toIndex - 1);
expandTo(endWordIndex);
long firstWordMask = WORD_MASK << fromIndex;
long lastWordMask = WORD_MASK >>> -toIndex;
if (startWordIndex == endWordIndex) {
// Case 1: One word
words[startWordIndex] |= (firstWordMask & lastWordMask);
} else {
// Case 2: Multiple words
// Handle first word
words[startWordIndex] |= firstWordMask;
// Handle intermediate words, if any
for (int i = startWordIndex+1; i < endWordIndex; i++)
words[i] = WORD_MASK;
// Handle last word (restores invariants)
words[endWordIndex] |= lastWordMask;
}
checkInvariants();
}
// 将from->to之间的所有值设置为传入的值,当传入的值为false的适合,调用的是下面的clear.
public void set(int fromIndex, int toIndex, boolean value) {
if (value)
set(fromIndex, toIndex);
else
clear(fromIndex, toIndex);
}
// 将范围内的bit置为0
public void clear(int fromIndex, int toIndex) {
checkRange(fromIndex, toIndex);
if (fromIndex == toIndex)
return;
int startWordIndex = wordIndex(fromIndex);
if (startWordIndex >= wordsInUse)
return;
int endWordIndex = wordIndex(toIndex - 1);
if (endWordIndex >= wordsInUse) {
toIndex = length();
endWordIndex = wordsInUse - 1;
}
long firstWordMask = WORD_MASK << fromIndex;
long lastWordMask = WORD_MASK >>> -toIndex;
if (startWordIndex == endWordIndex) {
// Case 1: One word
words[startWordIndex] &= ~(firstWordMask & lastWordMask);
} else {
// Case 2: Multiple words
// Handle first word
words[startWordIndex] &= ~firstWordMask;
// Handle intermediate words, if any
for (int i = startWordIndex+1; i < endWordIndex; i++)
words[i] = 0;
// Handle last word
words[endWordIndex] &= ~lastWordMask;
}
recalculateWordsInUse();
checkInvariants();
}
复制代码
这里有一个需要注意点,那就是当传入的值为 true/fasle 的时候,处理逻辑是不同的.具体的逻辑见上面简陋版本中的示例.
get方法
BitSet提供了一个获取单个位置bit值的方法,以及一个范围获取,返回一个新的BitSet的方法.
// 获取某个位置的bit值
public boolean get(int bitIndex) {
if (bitIndex < 0)
throw new IndexOutOfBoundsException("bitIndex < 0: " + bitIndex);
checkInvariants();
int wordIndex = wordIndex(bitIndex);
return (wordIndex < wordsInUse)
&& ((words[wordIndex] & (1L << bitIndex)) != 0);
}
// 返回一个子集,包含传入范围内的bit
public BitSet get(int fromIndex, int toIndex) {
checkRange(fromIndex, toIndex);
checkInvariants();
int len = length();
// If no set bits in range return empty bitset
if (len <= fromIndex || fromIndex == toIndex)
return new BitSet(0);
// An optimization
if (toIndex > len)
toIndex = len;
BitSet result = new BitSet(toIndex - fromIndex);
int targetWords = wordIndex(toIndex - fromIndex - 1) + 1;
int sourceIndex = wordIndex(fromIndex);
boolean wordAligned = ((fromIndex & BIT_INDEX_MASK) == 0);
// Process all words but the last word
for (int i = 0; i < targetWords - 1; i++, sourceIndex++)
result.words[i] = wordAligned ? words[sourceIndex] :
(words[sourceIndex] >>> fromIndex) |
(words[sourceIndex+1] << -fromIndex);
// Process the last word
long lastWordMask = WORD_MASK >>> -toIndex;
result.words[targetWords - 1] =
((toIndex-1) & BIT_INDEX_MASK) < (fromIndex & BIT_INDEX_MASK)
? /* straddles source words */
((words[sourceIndex] >>> fromIndex) |
(words[sourceIndex+1] & lastWordMask) << -fromIndex)
:
((words[sourceIndex] & lastWordMask) >>> fromIndex);
// Set wordsInUse correctly
result.wordsInUse = targetWords;
result.recalculateWordsInUse();
result.checkInvariants();
return result;
}
复制代码
逻辑操作
JDK实现的位图当然是有逻辑操作的,主要支持了 与,或,异或,与非 四种操作,由于代码不难,这里就不贴代码了,简略的贴一下API.
// 与操作
public void and(BitSet set);
// 或操作
public void or(BitSet set);
// 异或操作
public void xor(BitSet set);
// 与非操作
public void andNot(BitSet set);
复制代码
到这里,BitSet的源码就读完了,但是有没有发现一个问题 ? 前面说的 稀疏数据 的问题并没有得到解决,别急,下面就来了.
EWAHCompressedBitmap
这是google开发的javaEWAH包中的一个类.名字中的 EWAH = Enhanced Word-Aligned Hybrid .而Compressed是指压缩.
复习一下 稀疏数据 的问题,假设我们在一个位图中,首先 set(1) ,然后 set(1亿) 会怎样?
我们使用JDK中的BitSet来试一下,在运行过程中打断点看一下内部的数组是什么样子.如下图:
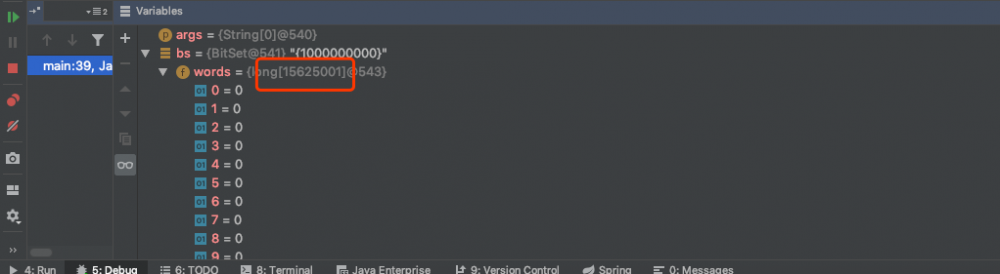
将其序列化输出到文件,文件大小如下图:

可以看到,我们为了保存1和1亿这两个数字,花费了一个一千多万长度的long数组,序列化后占用内存将近200m.这是不科学的.
接下来就是 EWAHCompressedBitmap 了,名字里面都带了压缩,那么想必表现不错.
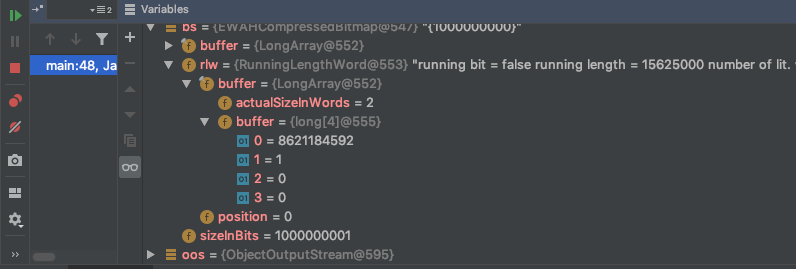

可以看到long数组的长度仅仅为4,且输出的文件大小为96byte.
这就很符合预期了.
在EWAHCompressedBitmap中,数据也是使用long数组来保存的,不过对每一个long有类别的定义, Literal Word 和 Running Length Word .
-
Literal Word: 存储真正的bit位. -
Running Length Word: 存储跨度信息.
什么是跨度信息呢? 举个例子:
在刚才使用BitSet存储1亿的时候,截图中long数组有一千多万个0,以及之后的一个值.
使用BitSet存储1和1亿(2048为虚拟值,不想算了):
| long | long | long | long | long | long | long | long | long | long | long | long |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ...1千万个0呢 | 0 | 0 | 2048 |
而在EWAHCompressedBitmap中,则是类似下面这样:
| long | long | long |
|---|---|---|
| 2 | 一千万个0 | 2048 |
这样看起来好像没什么区别....但是在BitSet中,一千万个0是真的使用了一千万个long来存储的.而在EWAHCompressedBitmap中,这个信息使用一个long来存储,long的值表示具体有多少个0在这个区间内.
这样子做,点题了.与名字中的压缩相对应. 将连续的0或者1进行压缩,以节省空间.
这样做有没有什么副作用呢?有的,当你的每一次插入都在一个 Running Length Word 上,也就是每一次插入都涉及到了 Running Length Word 的分裂,会降级性能,因此官方建议最好数据的插入从小到大进行.
EWAHCompressedBitmap基本解决了稀疏数据的问题,而当数据很稠密的时候,他的压缩率没有那么好,但是通常也不会差于不压缩的存储方式,因此在日常的使用中,还是建议大家使用这个类,除非你很清楚且能确保自己的数据不会过于 稀疏 .
总结
在本节,我们手动实现了一个极其简陋的位图,然后阅读了JDK中位图实现类 BitSet 的源码,然后分析了如何使用 EWAHCompressedBitmap 来解决稀疏数据的问题,对于 EWAHCompressedBitmap 的源码具体实现没有详细分析,有兴趣的朋友可以自己去查看.
Java语言使用者广泛,因此对于位图的实现,网上各种版本都有,既有大厂维护的开源版本,也有个人编写的版本.在使用时也不用完全局限于EWAHCompressedBitmap,可以使用各种魔改版本,由于位图的实现逻辑不是特别复杂,因此在使用前清楚其具体的实现逻辑即可.
Redis中的位图
这是redis官网对位图的介绍,很短... .
Redis是支持位图的,但是位图并不是一个单独的数据结构,而是在String类型上定义的一组面向位的操作指令.也就是说,当你使用Redis位图时,其实底层存储的是Redis的string类型.因此:
- 由于Redis的string是二进制安全的,所以用它当做位图的存储方式是可行的.
- Redis 的String类型最大是512Mb.所以Redis的单个位图只能存储2的32个次方个int.这应该是够用了.(不够用的话可以分key,用前缀来搞.)
- 由于底层是string,因此redis是没有对稀疏数据进行处理的,因此在使用时要额外注意这一点,防止这个key拖垮redis服务器.
Redis支持的操作如下:
- getbit : 获取某个key的某个位置的值.
getbit key offset. - setbit : 设置某个位置的值.
setbit key offset value. - bitcount : 计算某个key中为1的bit数量.支持范围.
bitcount key start end - bitpos : 返回范围内第一个为特定bit的位置.
bitpos key bit(0/1) start end - bitop : 逻辑运算,支持四种逻辑运算,和上面
BitSet支持的四种一样,具体的命令如下:
BITOP AND destkey srckey1 srckey2 srckey3 ... srckeyN BITOP OR destkey srckey1 srckey2 srckey3 ... srckeyN BITOP XOR destkey srckey1 srckey2 srckey3 ... srckeyN BITOP NOT destkey srckey 复制代码
其中destkey是结果存储的key,其余的srckey是参与运算的来源.
应用场景
应用场景其实是很考验人的,不能学以致用,在程序员行业里基本上就相当于没有学了吧...
经过自己的摸索以及在网上的浏览,大致见到了一些应用场景,粗略的写出来,方便大家理解并且以后遇到类似的场景可以想到位图并应用他!
用户签到/抢购等唯一限制
用户签到每天只能一次,抢购活动中只能购买一件,这些需求导致的有一种查询请求, 给定的id做没做过某事 .而且一般这种需求都无法接受你去查库的延迟.当然你查一次库之后在redis中写入: key = 2345 , value = 签到过了 .也是可以实现的,但是内存占用太大.
而使用位图之后,当 2345 用户签到过/抢购过之后,在redis中调用 setbit 2019-07-01-签到 2345 1 即可,之后用户的每次签到/抢购请求进来,只需要执行相应的getbit即可拿到是否放行的bool值.
这样记录,不仅可以节省空间,以及加快访问速度之外,还可以提供一些额外的统计功能,比如调用 bitcount 来统计今天签到总人数等等.统计速度一般是优于关系型数据库的,可以用来做实时的接口查询等.
用户标签等数据
大数据已经很普遍了,用户画像大家也都在做,这时候需要根据标签分类用户,进行存储.方便后续的推荐等操作.
而用户及标签的数据结构设计是一件比较麻烦的事情,且很容易造成查询性能太低.同时,对多个标签经常需要进行逻辑操作,比如喜欢电子产品的00后用户有哪些,女性且爱旅游的用户有哪些等等,这在关系型数据库中都会造成处理的困难.
可以使用位图来进行存储,每一个标签存储为一个位图(逻辑上,实际上你还可以按照尾号分开等等操作),在需要的时间进行快速的统计及计算. 如:
| 用户 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| 爱旅游 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
可以清晰的统计出, 0,3,6 用户喜欢旅游.
| 用户 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| 00后 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
用户 0,1,6 是00后.
那么对两个位图取与即可得到爱旅游的00后用户为 0,6 .
2019-07-02 完成











![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)

