转载

你确定不来了解下 Redis 跳跃表的原理吗

前言

本章将介绍 Redis中 set 和 zset的基本使用和内部原理.因为这两种数据结构有很多相似的地方所以把他们放到一章中介绍.并且重点介绍zset 内部一个很重要的数据结构:跳跃表.

基本介绍

set

先来看看 set

Redis 中 set 集合很像Java 中 HashSet,键值对无序、唯一、不为空.

> sadd books Java
(integer 1)
> sadd books Java
(integer 0)            # value 值重复
> sadd books Go
(integer 1)
> smembers books        # 无序
1) "Go"
2) "Java"

zset

zset 是 Redis 中最特别的基础数据结构,其他几个都能和 Java 大致对应上.它基本上还是一个 set 但是添加了一个 score 属性去保证有序性.其内部实现为跳跃表稍后将会着重介绍.

> zadd books 1 Java
(integer) 1
> zadd books 2 Go
(integer) 1
> zadd books 3 Python
(integer) 1
> zrange books 0 -1     #按 score 有序取出
1) "Java"
2) "Go"
3) "Python"

在 zset 中 score 的类型为 double 所以有时会出现小数点精度问题.

当 zset 中最后一个 value 被删除后,这个和 zset 就会被自动删除,内存被回收.

内部原理

Redis 的 zset 是个复合结构,是由一个 hash 和 skiplist 组成的,其中 hash 用来保存 value 和 score 对应关系.skiplist 用来给 score 排序.关于hash 的内部实现请参阅之前的一篇文章: 《你确定不来了解一下Redis中 Hash的原理吗》 ,在这里我们着重介绍 skiplist 的实现.

skiplist 跳跃表

因为zset需要高效的插入和删除,所以底层不适合使用数组实现,需要使用链表的结构.当插入新元素时需要根据 score插入到链表合适的位置,保证链表的有序性.高效的办法是通过二分查找去找到插入点.

那么问题就来了,二分查找的对象必须是有序数组,只有数组支持快速定位,链表做不到该怎么办呢?这时,就该跳跃表出场了.

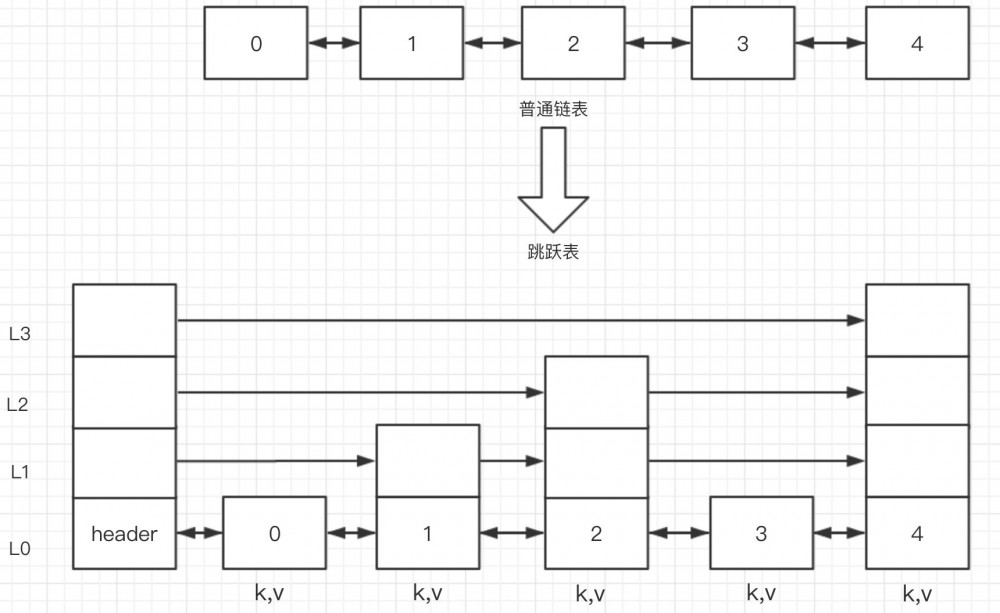
你确定不来了解下 Redis 跳跃表的原理吗

如图所示,跳跃表在链表的基础上加入了层级L0~L3的概念,Redis 的跳跃表共有 64 层,可容纳 $2^{64}$ 个元素.每个元素的层级是随机分配的,分配 L0 的概率是 100%,就是说每个元素至少会有一层.分配L1 的概率是 50%,分配 L2 的概率是 25%,往上以此类推.

每个 kv 对应的结构为zslnode.kv 之间使用指针形成有序的双向链表.同一层的 kv 会使用指针串起来.每层元素的遍历都是从跳跃表的头指针 kv header 出发.

header 的结构也是 zslnode,当中 value 为 null,score 为 Double.MIN_VALUE排在最前面.

struct zslnode{
    string value;
    double score;
    zslnode*[] forwards;    //多层连接的指针
    zslnode* backward;        //回溯指针
}

struct zsl{
    zslnode* header;            //跳跃表头指针
    int maxLevel;                //当前节点的最高层
    map<String,zslnode*> ht;    //hash 中的键值对
}