LeetCode 第703题 Kth Largest Element in a Stream 【堆】Java
原题地址: https://leetcode.com/problems/kth-largest-element-in-a-stream/
设计一个类寻找一个数据流里面的第 k 大的元素。注意是指排序后的第k大元素,而不是第k个不重复元素。
你的 KthLargest 类应该有一个构建器接受一个整数 k 和一个整数数组 nums ,包含流的初始元素。每次调用方法 KthLargest.add ,返回流里面的第 k 大的元素。
例子:
int k = 3; int[] arr = [4,5,8,2]; KthLargest kthLargest = new KthLargest(3, arr); kthLargest.add(3); // returns 4 kthLargest.add(5); // returns 5 kthLargest.add(10); // returns 5 kthLargest.add(9); // returns 8 kthLargest.add(4); // returns 8
注意:
你可以假定 nums 的长度 ≥ k-1 而且 k ≥ 1 。
解决方案1:一个最大堆加一个最小堆
这类题目肯定可以想到堆,但是做起来稍微有点麻烦。我们思考这个题,会发现,首先我们一开始可以构建一个最大堆,这样我们就得到最初始的的最大k个元素。
然后如果add的新的数字小于当前的第k个最大元素,那么这个add操作对结果毫无影响,第k个最大元素没变。如果,add的新数字比当前的第k个最大元素大,我们就会发现它会被当前的第k个最大元素挤走。
所以,我们可以用一个最小堆来保存k个最大的元素。如果新加的数字小于等于最小堆的最小元素,则不做任何修改,输出最小堆的最小元素即可。
如果新加的元素比较大,我们就用它替换堆的第一个元素(堆顶,即最小值),然后minHeapify(1),这样最小堆就可以又保证最小值在堆顶了。
所以构建器的代码如下:

add方法代码:

这个实现里用的是我们之前提到的最大堆最小堆的标准实现,只是给最小堆类加了一个方法replaceTop:

最后耗时为60毫秒,好于66.06%的Java代码。
解决方案2:一个最小堆
仔细思考方案1后我们发现,最大堆是多余的。一个最小堆也可以解决问题。首先我们把一个k大小的数组全部成员初始化为Integer.MIN_VALUE。然后把它构建成一个最小堆,然后用我们之前实现的add方法加入全部元素,我们会发现堆里面就是最大的k个元素。然后继续用add动态加入新的数字,也不会影响这一特性。其实复杂度差异不大,但是代码就简单多了。add和replaceTop都不用修改,只需要实现一个新的构造器即可。
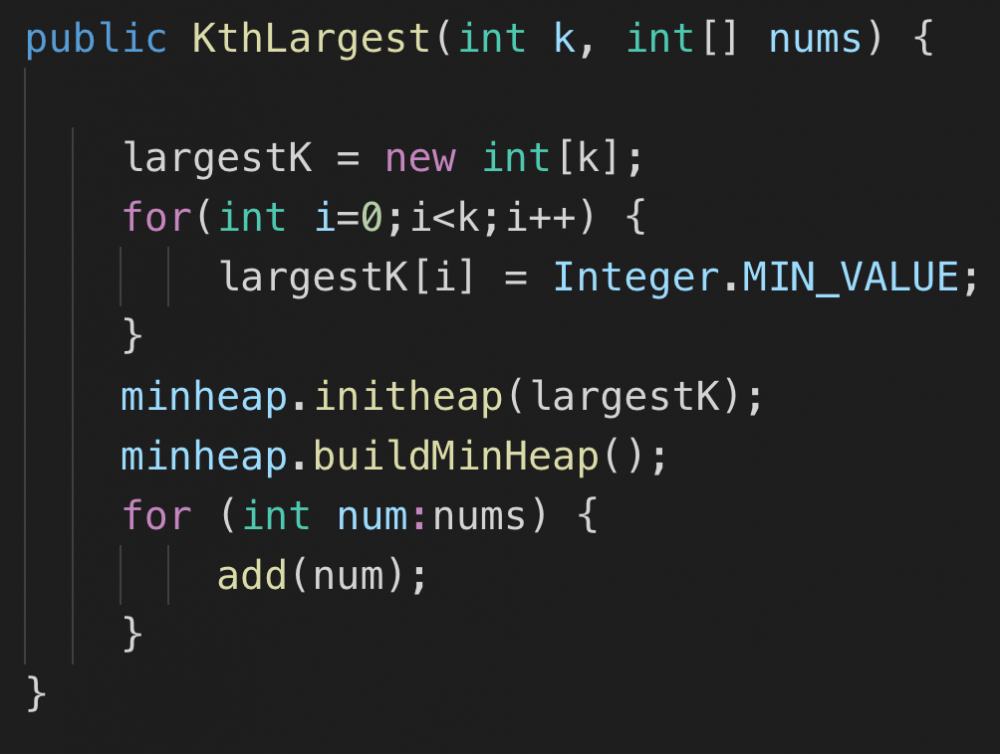
代码地址: https://github.com/tinyfool/leetcode/tree/master/src/p0703
也请参阅《 Leetcode专题 堆结构和堆排序 》,文章介绍了堆和堆排序,以及最大堆的实现。











![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)

