转载

史上最详尽 Java 8 集合类 HashMap : 底层实现和原理学习笔记（源码解析）

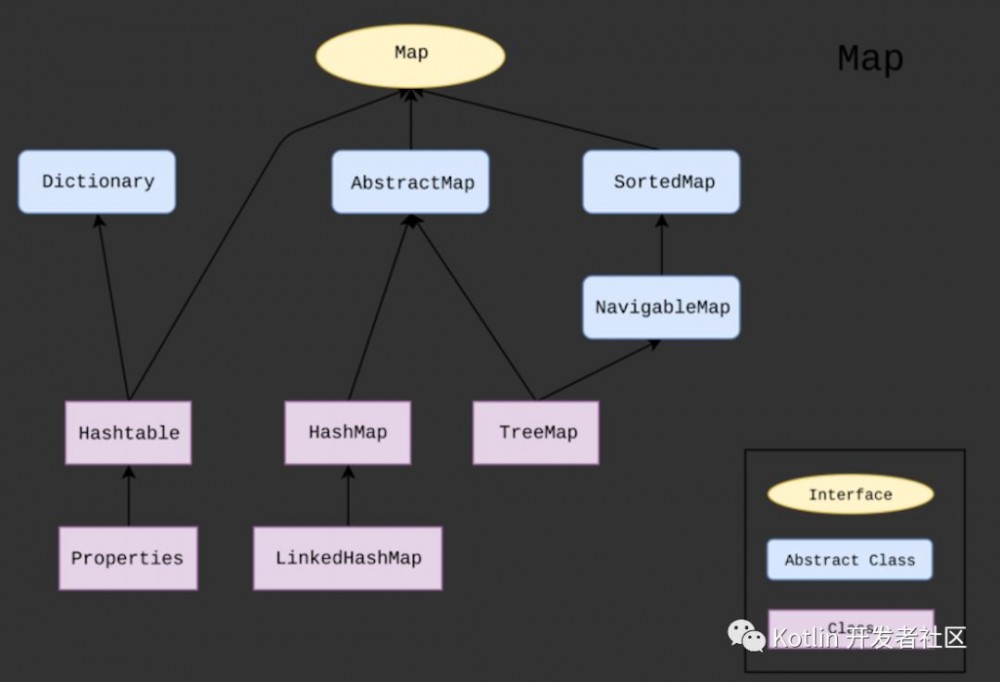
Java中Map接口集合类继承关系

在 Java 中，最基本的结构就是两种，一个是数组，另外一个是模拟指针（引用），所有的数据结构都可以用这两个基本结构来构造的，HashMap也不例外。Hashmap实际上是一个数组和链表的结合体（在数据结构中，一般称之为“链表散列“），请看下图: [ https://www.iteye.com/topic/539465 ]

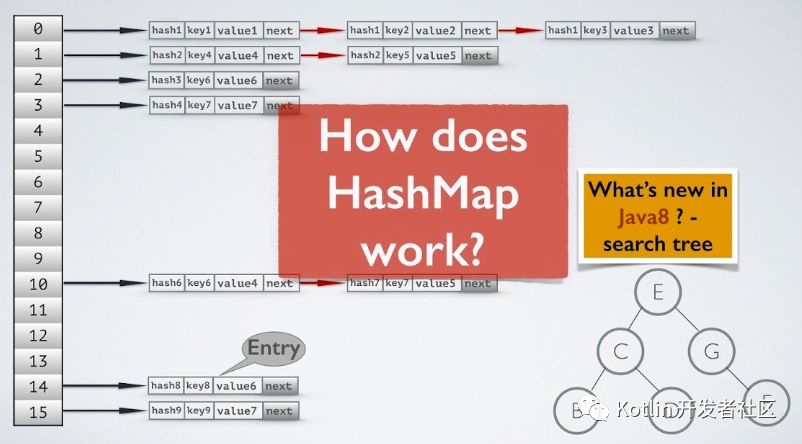
Map 接口基于哈希表实现。Map 中并允许空值和空键。

HashMap 类大致相当于 Hashtable，只是它不是同步的, 且允许空值。在Hashtable中方法都加上了 synchronized:

public class Hashtable<K,V>

extends Dictionary<K,V>

implements Map<K,V>, Cloneable, java.io.Serializable {

...

public synchronized int size(){}

public synchronized boolean isEmpty(){}

public synchronized Enumeration<K> keys(){}

public synchronized Enumeration<V> elements(){}

public synchronized boolean contains(Object value) {}

public synchronized boolean containsKey(Object key) {}

public synchronized V get(Object key) {}

public synchronized V put(K key, V value) {}

public synchronized V remove(Object key) {}

public synchronized void putAll(Map<? extends K, ? extends V> t) {}

public synchronized void clear() {}

public synchronized Object clone() {}

public synchronized String toString() {}

...

public synchronized int hashCode() {}

public synchronized V getOrDefault(Object key, V defaultValue) {}

public synchronized void forEach(BiConsumer<? super K, ? super V> action) {}

public synchronized void replaceAll(BiFunction<? super K, ? super V, ? extends V> function) {}

public synchronized V putIfAbsent(K key, V value) {}

public synchronized boolean remove(Object key, Object value) {}

public synchronized boolean replace(K key, V oldValue, V newValue) {}

public synchronized V replace(K key, V value) {}

public synchronized V computeIfAbsent(K key, Function<? super K, ? extends V> mappingFunction) {}

public synchronized V computeIfPresent(K key, BiFunction<? super K, ? super V, ? extends V> remappingFunction) {}

public synchronized V compute(K key, BiFunction<? super K, ? super V, ? extends V> remappingFunction) {}

public synchronized V merge(K key, V value, BiFunction<? super V, ? super V, ? extends V> remappingFunction) {}

Hash table based implementation of the Map interface. This implementation provides all of the optional map operations, and permits null values and the null key. (The HashMap class is roughly equivalent to Hashtable, except that it is unsynchronized and permits nulls.) This class makes no guarantees as to the order of the map; in particular, it does not guarantee that the order will remain constant over time.

Unlike HashMap, Hashtable does not support null values and null keys because there is null check in the put method implementation of Hashtable.

史上最详尽 Java 8 集合类 HashMap : 底层实现和原理学习笔记（源码解析）

HashMap是乱序的，HashMap 本身不保证映射中元素的顺序；也就是说, 顺序会随着时间的推移而变化。

如果想要保持顺序, 可使用 LinkedHashMap:

public class LinkedHashMap<K,V>

extends HashMap<K,V>

implements Map<K,V>

{}

此实现与 HashMap 的不同之处在于，后者维护着一个运行于所有条目的双重链接列表( doubly linked list ) 。此链接列表定义了迭代顺序，该迭代顺序通常就是将键插入到映射中的顺序（插入顺序）。

史上最详尽 Java 8 集合类 HashMap : 底层实现和原理学习笔记（源码解析）

HashMap 实现了 Map接口. 这个Map接口设计(@author Josh Bloch)如下:

<strong style="white-space:normal;font-size:18px;font-family:mp-quote, -apple-system-font, BlinkMacSystemFont, "Helvetica Neue", "PingFang SC", "Hiragino Sans GB", "Microsoft YaHei UI", "Microsoft YaHei", Arial, sans-serif;"></strong>

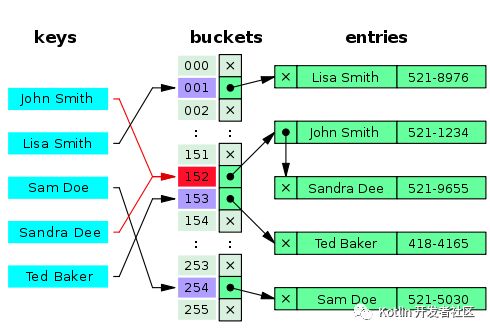
史上最详尽 Java 8 集合类 HashMap : 底层实现和原理学习笔记（源码解析）

一、先来熟悉一下我们常用的HashMap( 基于JDK1.7) :

[https://www.cnblogs.com/java-jun-world2099/p/9258605.html]

1、概述

HashMap基于Map接口实现，元素以键值对的方式存储，并且允许使用null 建和null值，因为key不允许重复，因此只能有一个键为null,另外HashMap不能保证放入元素的顺序，它是无序的，和放入的顺序并不能相同。HashMap是线程不安全的。

2、继承关系

public class HashMap<K,V>extends AbstractMap<K,V>
    implements Map<K,V>, Cloneable, Serializable

3、基本属性

static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; //默认初始化大小 16
static final float DEFAULT_LOAD_FACTOR = 0.75f;     //负载因子0.75
static final Entry<?,?>[] EMPTY_TABLE = {};         //初始化的默认数组
transient int size;     //HashMap中元素的数量
int threshold;          //判断是否需要调整HashMap的容量

Note：HashMap的扩容操作是一项很耗时的任务，所以如果能估算Map的容量，最好给它一个默认初始值，避免进行多次扩容。HashMap的线程是不安全的，多线程环境中推荐是ConcurrentHashMap。

构造函数

HashMap() 构造函数, 使用默认初始容量（16）和默认加载因子（0.75）构造一个空的 HashMap 。

/**

* Constructs an empty <tt>HashMap</tt> with the specified initial

* capacity and load factor.

* @param initialCapacity the initial capacity

* @param loadFactor the load factor

* @throws IllegalArgumentException if the initial capacity is negative

* or the load factor is nonpositive

public HashMap(int initialCapacity, float loadFactor) {

//以下三个if判断都是对容量和加载因子进行过滤

if (initialCapacity < 0)

throw new IllegalArgumentException("Illegal initial capacity: " + initialCapacity);

if (initialCapacity > MAXIMUM_CAPACITY)

initialCapacity = MAXIMUM_CAPACITY;

if (loadFactor <= 0 || Float.isNaN(loadFactor))

throw new IllegalArgumentException("Illegal load factor: " + loadFactor);

// Find a power of 2 >= initialCapacity

int capacity = 1;

while (capacity < initialCapacity)

capacity <<= 1; // 扩容: 2 的 n 幂次方

this.loadFactor = loadFactor;

//threshold就是hashmap的元素数量临界值，元素数量达到这个值，就会扩容。是否要扩容操在添加元素的时候进行判断。

threshold = (int)Math.min(capacity * loadFactor, MAXIMUM_CAPACITY + 1);

//重点：创建了一个容量为capacity的数组

table = new Entry[capacity];

//是否使用备选哈希函数，用来对key为String类型的hash函数进行特殊处理，减少hash值的碰撞。

useAltHashing = sun.misc.VM.isBooted() &&(capacity >= Holder.ALTERNATIVE_HASHING_THRESHOLD);

init();

}

注意到构造函数中，创建了一个Entry类型的数组。这个数组就是用来存放元素的，而元素在数组中的位置是由元素key的哈希值计算的(后面会介绍)。当元素key的哈希值冲突怎么办呢？HashMap 将数组元素设计成了单链表。我们来看看Entry的结构到底是不是一个单链表。

static class Entry<K,V> implements Map.Entry<K,V> {

final K key;

V value;

Entry<K,V> next;

int hash;

/**

* Creates new entry.

Entry(int h, K k, V v, Entry<K,V> n) {

value = v;

next = n;

key = k;

hash = h;

}

...

}

可以看到有一个Entry类型的next变量就是存放下一个结点的。那么我们再看一看HashMap的put函数，进一步验证。

/**

* Associates the specified value with the specified key in this map.

* If the map previously contained a mapping for the key, the old

* value is replaced.

* @param key key with which the specified value is to be associated

* @param value value to be associated with the specified key

* @return the previous value associated with <tt>key</tt>, or

* <tt>null</tt> if there was no mapping for <tt>key</tt>.

* (A <tt>null</tt> return can also indicate that the map

* previously associated <tt>null</tt> with <tt>key</tt>.)

public V put(K key, V value) {

//将key为null的元素，单独处理，放在了数组下标为0的位置,下面有putForNullKey函数的源码。

if (key == null)

return putForNullKey(value);

//重新计算一遍hash值: 精髓一

int hash = hash(key);

//根据新计算出的hash值，找到对应的数组下标i，先忽略，后面会详细讲。

int i = indexFor(hash, table.length);

//下面就是遍历单链表了，查找是否有key相同的元素，key如果相同，就是将value进行替换。

for (Entry<K,V> e = table[i]; e != null; e = e.next) {

Object k;

if (e.hash == hash && ((k = e.key) == key || key.equals(k))) {

V oldValue = e.value;

e.value = value;

e.recordAccess(this);

return oldValue;

}

modCount++;

//没有找到key相同的元素，那么就是在单链表表头添加一个新元素。下面会贴上addEnry函数的源码。

addEntry(hash, key, value, i);

return null;

}

/**

* Offloaded version of put for null keys

private V putForNullKey(V value) {

//这部分代码也很容易理解，就是在数组第一个位置插入元素，先判断key是否为null,再将value进行替换。因为数组下标为0的位置也有可能key不为null。但是key为null的元素一定是放在了数组下标为0的位置。

for (Entry<K,V> e = table[0]; e != null; e = e.next) {

if (e.key == null) {

V oldValue = e.value;

e.value = value;

e.recordAccess(this);

return oldValue;

}

modCount++;

addEntry(0, null, value, 0);

return null;

}

可以看到，put函数中允许了key为null值的元素，并且将key为null的元素放在了数组下标为0的位置。下面，我们接着看addEntry函数的源码。

/**

* Adds a new entry with the specified key, value and hash code to

* the specified bucket. It is the responsibility of this

* method to resize the table if appropriate.

* Subclass overrides this to alter the behavior of put method.

void addEntry(int hash, K key, V value, int bucketIndex) {

//当元素数量达到临界值，就会进行扩容操作，新的容量是原来容量的两倍。

if ((size >= threshold) && (null != table[bucketIndex])) {

resize(2 * table.length);

hash = (null != key) ? hash(key) : 0;

bucketIndex = indexFor(hash, table.length);

}

//创建新的元素

createEntry(hash, key, value, bucketIndex);

}

/**

* Like addEntry except that this version is used when creating entries

* as part of Map construction or "pseudo-construction" (cloning,

* deserialization). This version needn't worry about resizing the table.

* Subclass overrides this to alter the behavior of HashMap(Map),

* clone, and readObject.

void createEntry(int hash, K key, V value, int bucketIndex) {

//下面是经典的单链表插入表头的算法：先将表头元素记录下来，再将新表头重新赋值。

Entry<K,V> e = table[bucketIndex];

table[bucketIndex] = new Entry<>(hash, key, value, e);

size++;

}

添加元素时，进行了容量判断，超过临界值就会扩容。扩容操作就是新建一个容量为原来两倍的数组，将原来的元素复制过来。讲到这里，HashMap的整体结构已经很清晰了。感兴趣的同学可以看一看查找元素的代码，阿楠就不作阐释了。

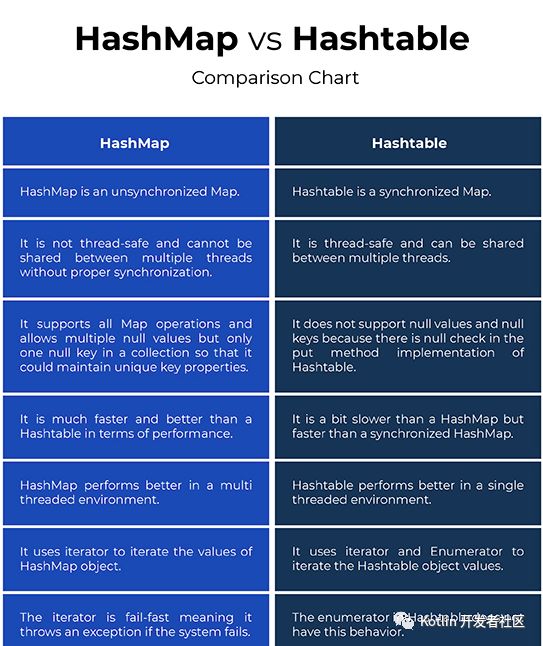
二、常被问到的HashMap和Hashtable的区别

1、线程安全

两者最主要的区别在于Hashtable是线程安全，而HashMap则非线程安全。

Hashtable的实现方法里面都添加了synchronized关键字来确保线程同步，因此相对而言HashMap性能会高一些，我们平时使用时若无特殊需求建议使用HashMap，在多线程环境下若使用HashMap需要使用Collections.synchronizedMap()方法来获取一个线程安全的集合。

Note：

Collections.synchronizedMap()实现原理是Collections定义了一个SynchronizedMap的内部类，这个类实现了Map接口，在调用方法时使用synchronized来保证线程同步,当然了实际上操作的还是我们传入的HashMap实例，简单的说就是Collections.synchronizedMap()方法帮我们在操作HashMap时自动添加了synchronized来实现线程同步，类似的其它Collections.synchronizedXX方法也是类似原理。

2、针对null的不同

HashMap可以使用null作为key，而Hashtable则不允许null作为key

虽说HashMap支持null值作为key，不过建议还是尽量避免这样使用，因为一旦不小心使用了，若因此引发一些问题，排查起来很是费事。

Note：HashMap以null作为key时，总是存储在table数组的第一个节点上。

3、继承结构

HashMap是对Map接口的实现，HashTable实现了Map接口和Dictionary抽象类。

4、初始容量与扩容

HashMap的初始容量为16，Hashtable初始容量为11，两者的填充因子默认都是0.75。

HashMap扩容时是当前容量翻倍即:capacity*2，Hashtable扩容时是容量翻倍+1即:capacity*2+1。

5、两者计算hash的方法不同

Hashtable计算hash是直接使用key的hashcode对table数组的长度直接进行取模

int hash = key.hashCode();
int index = (hash & 0x7FFFFFFF) % tab.length;

HashMap计算hash对key的hashcode进行了二次hash，以获得更好的散列值，然后对table数组长度取摸。

int hash = hash(key.hashCode());
int i = indexFor(hash, table.length);

static int hash(int h) {
        // This function ensures that hashCodes that differ only by
        // constant multiples at each bit position have a bounded
        // number of collisions (approximately 8 at default load factor).
        h ^= (h >>> 20) ^ (h >>> 12);
        return h ^ (h >>> 7) ^ (h >>> 4);
    }
 
 static int indexFor(int h, int length) {

return h & (length-1);

哈希函数：hash()

hash() 方法是HashMap 中的核心函数，在存储数据时，将key传入中进行运算，得出key的哈希值，通过这个哈希值运算才能获取key应该放置在 “桶” 的哪个位置，下面是方法的源码：

static final int hash(Object key) {

int h;

return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);

从源码中可以看出，传入key之后，hash() 会获取key的hashCode进行无符号右移 16 位，然后进行按位异或，并把运算后的值返回，这个值就是key的哈希值。这样运算是为了减少碰撞冲突，因为大部分元素的hashCode在低位是相同的，不做处理的话很容易造成冲突。

之后还需要把 hash() 的返回值与table.length - 1做与运算，得到的结果即是数组的下标(为什么这么算，下面会说)，在上面的 putVal() 方法中就可以看到有这样的代码操作，举个例子图：

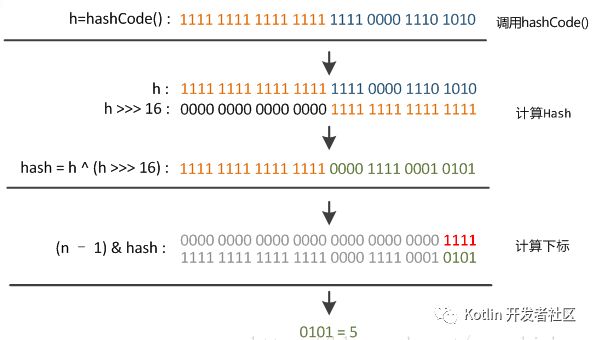
史上最详尽 Java 8 集合类 HashMap : 底层实现和原理学习笔记（源码解析）

table.length - 1就像是一个低位掩码（这个设计也优化了扩容操作的性能），它和hash()做与操作时必然会将高位屏蔽（因为一个HashMap不可能有特别大的buckets数组，至少在不断自动扩容之前是不可能的，所以table.length - 1的大部分高位都为0），只保留低位，这样一来就总是只有最低的几位是有效的，就算你的hashCode()实现得再好也难以避免发生碰撞。这时，hash()函数的价值就体现出来了，它对hash code的低位添加了随机性并且混合了高位的部分特征，显著减少了碰撞冲突的发生。

另外，在putVal方法的源码中，我们可以看到有这样一段代码

if ((p = tab[i = (n - 1) & hash]) == null)

tab[i] = newNode(hash, key, value, null);

这里检测要插入位置是否有元素，没有的话直接新建一个包含key的节点.

那么这里为什么要用 i = (n - 1) & hash 作为索引运算呢？

这其实是一种优化手段，由于数组的大小永远是一个2次幂，在扩容之后，一个元素的新索引要么是在原位置，要么就是在原位置加上扩容前的容量。这个方法的巧妙之处全在于&运算，之前提到过&运算只会关注 n – 1（n = 数组长度）的有效位，当扩容之后，n的有效位相比之前会多增加一位（n会变成之前的二倍，所以确保数组长度永远是2次幂很重要），然后只需要判断hash在新增的有效位的位置是0还是1就可以算出新的索引位置，如果是0，那么索引没有发生变化，如果是1，索引就为原索引加上扩容前的容量。(http://www.importnew.com/29724.html) 效果图如下：

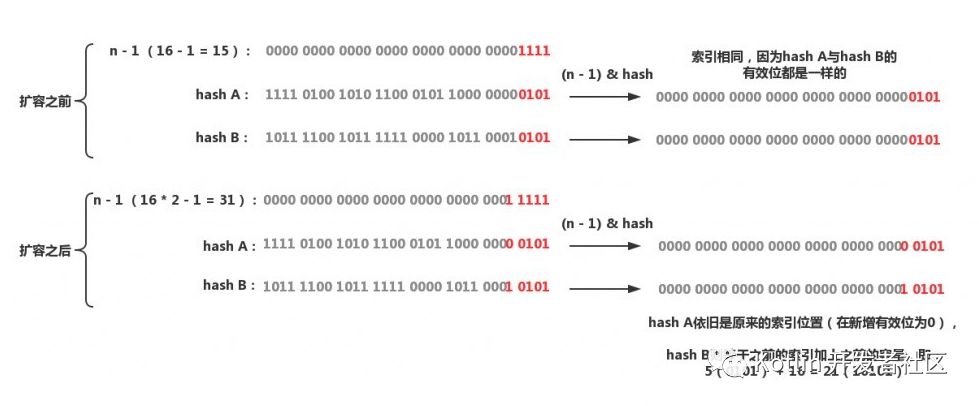
史上最详尽 Java 8 集合类 HashMap : 底层实现和原理学习笔记（源码解析）

这样在每次扩容时都不用重新计算hash，省去了不少时间，而且新增有效位是0还是1是带有随机性的，之前两个碰撞的Entry又有可能在扩容时再次均匀地散布开，真可谓是非常精妙的设计。

[https://blog.csdn.net/yeyazhishang/article/details/83114658]

三、HashMap的数据存储结构

1、HashMap由数组和链表来实现对数据的存储

HashMap采用Entry数组来存储key-value对，每一个键值对组成了一个Entry实体，Entry类实际上是一个单向的链表结构，它具有Next指针，可以连接下一个Entry实体，以此来解决Hash冲突的问题。

数组存储区间是连续的，占用内存严重，故空间复杂的很大。但数组的二分查找时间复杂度小，为O(1)；数组的特点是：寻址容易，插入和删除困难；

链表存储区间离散，占用内存比较宽松，故空间复杂度很小，但时间复杂度很大，达O（N）。链表的特点是：寻址困难，插入和删除容易。

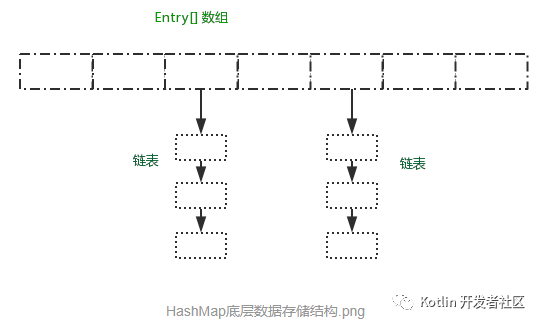
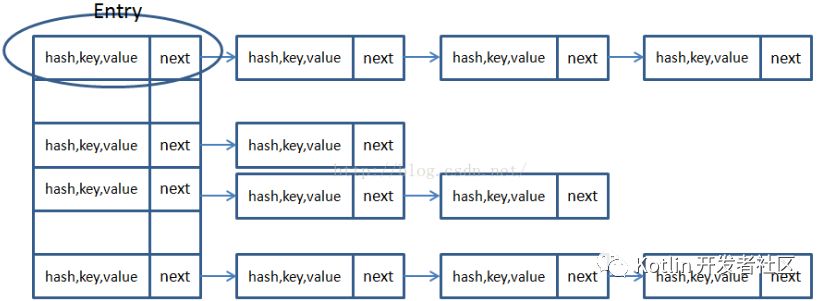
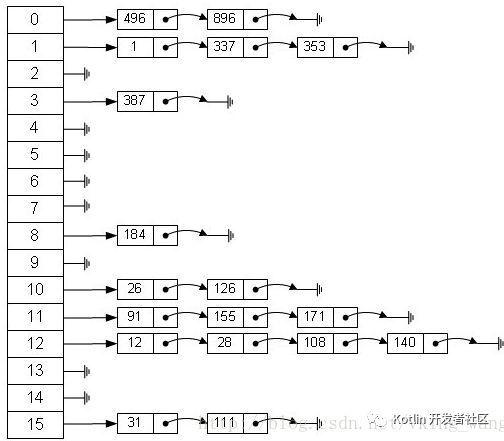
史上最详尽 Java 8 集合类 HashMap : 底层实现和原理学习笔记（源码解析）

从上图我们可以发现数据结构由 数组+链表 组成，一个长度为16的数组中，每个元素存储的是一个链表的头结点。那么这些元素是按照什么样的规则存储到数组中呢。一般情况是通过hash(key.hashCode())%len获得，也就是元素的key的哈希值对数组长度取模得到。比如上述哈希表中，12%16=12,28%16=12,108%16=12,140%16=12。所以12、28、108以及140都存储在数组下标为12的位置。

HashMap里面实现一个静态内部类Entry，其重要的属性有 hash，key，value，next。

HashMap里面用到链式数据结构的一个概念。上面我们提到过Entry类里面有一个next属性，作用是指向下一个Entry。打个比方，第一个键值对A进来，通过计算其key的hash得到的index=0，记做:Entry[0] = A。一会后又进来一个键值对B，通过计算其index也等于0，现在怎么办？HashMap会这样做: B.next = A ,Entry[0] = B,如果又进来C,index也等于0,那么 C.next = B ,Entry[0] = C；这样我们发现index=0的地方其实存取了A,B,C三个键值对,他们通过next这个属性链接在一起。所以疑问不用担心。 也就是说数组中存储的是最后插入的元素。 到这里为止，HashMap的大致实现，我们应该已经清楚了。

public V put(K key, V value) {
        if (key == null)
            return putForNullKey(value); //null总是放在数组的第一个链表中
        int hash = hash(key.hashCode());
        int i = indexFor(hash, table.length);
        //遍历链表
        for (Entry<K,V> e = table[i]; e != null; e = e.next) {
            Object k;
            //如果key在链表中已存在，则替换为新value
            if (e.hash == hash && ((k = e.key) == key || key.equals(k))) {
                V oldValue = e.value;
                e.value = value;
                e.recordAccess(this);
                return oldValue;
            }
        }
 
        modCount++;
        addEntry(hash, key, value, i);
        return null;
    }

 

void addEntry(int hash, K key, V value, int bucketIndex) {
    Entry<K,V> e = table[bucketIndex];
    table[bucketIndex] = new Entry<K,V>(hash, key, value, e); //参数e, 是Entry.next
    //如果size超过threshold，则扩充table大小。再散列
    if (size++ >= threshold)
            resize(2 * table.length);
}

四、重要方法深度解析

1、构造方法

HashMap()    //无参构造方法
HashMap(int initialCapacity)  //指定初始容量的构造方法
HashMap(int initialCapacity, float loadFactor) //指定初始容量和负载因子
HashMap(Map<? extends K,? extends V> m)  //指定集合，转化为HashMap

HashMap提供了四个构造方法，构造方法中，依靠第三个方法来执行的，但是前三个方法都没有进行数组的初始化操作，即使调用了构造方法此时存放HaspMap中数组元素的table表长度依旧为0 。在第四个构造方法中调用了inflateTable()方法完成了table的初始化操作，并将m中的元素添加到HashMap中。

2、添加方法

public V put(K key, V value) {
        if (table == EMPTY_TABLE) { //是否初始化
            inflateTable(threshold);
        }
        if (key == null) //放置在0号位置
            return putForNullKey(value);
        int hash = hash(key); //计算hash值
        int i = indexFor(hash, table.length);  //计算在Entry[]中的存储位置
        for (Entry<K,V> e = table[i]; e != null; e = e.next) {
            Object k;
            if (e.hash == hash && ((k = e.key) == key || key.equals(k))) {
                V oldValue = e.value;
                e.value = value;
                e.recordAccess(this);
                return oldValue;
            }
        }

        modCount++;
        addEntry(hash, key, value, i); //添加到Map中
        return null;
}

在该方法中，添加键值对时，首先进行table是否初始化的判断，如果没有进行初始化（分配空间，Entry[]数组的长度）。然后进行key是否为null的判断，如果key==null ,放置在Entry[]的0号位置。计算在Entry[]数组的存储位置，判断该位置上是否已有元素，如果已经有元素存在，则遍历该Entry[]数组位置上的单链表。判断key是否存在，如果key已经存在，则用新的value值，替换点旧的value值，并将旧的value值返回。如果key不存在于HashMap中，程序继续向下执行。将key-vlaue, 生成Entry实体，添加到HashMap中的Entry[]数组中。

3、addEntry()

* hash hash值

* key 键值

* value value值

* bucketIndex Entry[]数组中的存储索引

* /

void addEntry(int hash, K key, V value, int bucketIndex) {

if ((size >= threshold) && (null != table[bucketIndex])) {

resize(2 * table.length); //扩容操作，将数据元素重新计算位置后放入newTable中，链表的顺序与之前的顺序相反

hash = (null != key) ? hash(key) : 0;

bucketIndex = indexFor(hash, table.length);

}

createEntry(hash, key, value, bucketIndex);

}

void createEntry(int hash, K key, V value, int bucketIndex) {

Entry<K,V> e = table[bucketIndex];

table[bucketIndex] = new Entry<>(hash, key, value, e);

size++;

}

添加到方法的具体操作，在添加之前先进行容量的判断，如果当前容量达到了阈值，并且需要存储到Entry[]数组中，先进性扩容操作，空充的容量为table长度的2倍。重新计算hash值，和数组存储的位置，扩容后的链表顺序与扩容前的链表顺序相反。然后将新添加的Entry实体存放到当前Entry[]位置链表的头部。在1.8之前，新插入的元素都是放在了链表的头部位置，但是这种操作在高并发的环境下容易导致死锁，所以1.8之后，新插入的元素都放在了链表的尾部。

4、获取方法：get

public V get(Object key) {
     if (key == null)
         //返回table[0] 的value值
         return getForNullKey();
     Entry<K,V> entry = getEntry(key);

     return null == entry ? null : entry.getValue();
}
final Entry<K,V> getEntry(Object key) {
     if (size == 0) {
         return null;
     }

     int hash = (key == null) ? 0 : hash(key);
     for (Entry<K,V> e = table[indexFor(hash, table.length)];
         e != null;
         e = e.next) {
         Object k;
         if (e.hash == hash &&
             ((k = e.key) == key || (key != null && key.equals(k))))
            return e;
      }
     return null;
}

在get方法中，首先计算hash值，然后调用indexFor()方法得到该key在table中的存储位置，得到该位置的单链表，遍历列表找到key和指定key内容相等的Entry，返回entry.value值。

5、删除方法

public V remove(Object key) {
     Entry<K,V> e = removeEntryForKey(key);
     return (e == null ? null : e.value);
}
final Entry<K,V> removeEntryForKey(Object key) {
     if (size == 0) {
         return null;
     }
     int hash = (key == null) ? 0 : hash(key);
     int i = indexFor(hash, table.length);
     Entry<K,V> prev = table[i];
     Entry<K,V> e = prev;

     while (e != null) {
         Entry<K,V> next = e.next;
         Object k;
         if (e.hash == hash &&
             ((k = e.key) == key || (key != null && key.equals(k)))) {
             modCount++;
             size--;
             if (prev == e)
                 table[i] = next;
             else
                 prev.next = next;
             e.recordRemoval(this);
             return e;
         }
         prev = e;
         e = next;
    }

    return e;
}

删除操作，先计算指定key的hash值，然后计算出table中的存储位置，判断当前位置是否Entry实体存在，如果没有直接返回，若当前位置有Entry实体存在，则开始遍历列表。定义了三个Entry引用，分别为pre, e ,next。在循环遍历的过程中，首先判断pre 和 e 是否相等，若相等表明，table的当前位置只有一个元素，直接将table[i] = next = null 。若形成了pre -> e -> next 的连接关系，判断e的key是否和指定的key 相等，若相等则让pre -> next ,e 失去引用。

6、containsKey

public boolean containsKey(Object key) {
        return getEntry(key) != null;
    }
final Entry<K,V> getEntry(Object key) {
        int hash = (key == null) ? 0 : hash(key.hashCode());
        for (Entry<K,V> e = table[indexFor(hash, table.length)];
             e != null;
             e = e.next) {
            Object k;
            if (e.hash == hash &&
                ((k = e.key) == key || (key != null && key.equals(k))))
                return e;
        }
        return null;
    }

containsKey方法是先计算hash然后使用hash和table.length取摸得到index值，遍历table[index]元素查找是否包含key相同的值。

7、containsValue

public boolean containsValue(Object value) {
    if (value == null)
            return containsNullValue();

    Entry[] tab = table;
        for (int i = 0; i < tab.length ; i++)
            for (Entry e = tab[i] ; e != null ; e = e.next)
                if (value.equals(e.value))
                    return true;
    return false;
    }

containsValue方法就比较粗暴了，就是直接遍历所有元素直到找到value，由此可见HashMap的containsValue方法本质上和普通数组和list的contains方法没什么区别，你别指望它会像containsKey那么高效。

五、JDK 1.8的改变

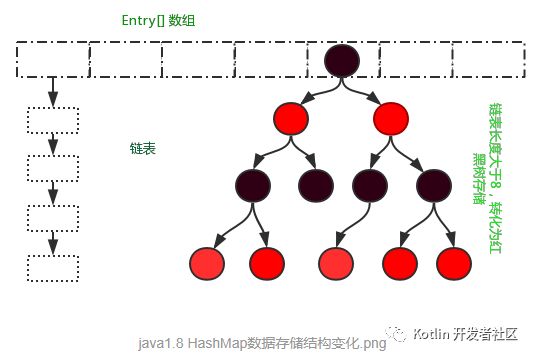
1、HashMap采用: "数组+链表(Node)+红黑树(TreeNode)" 实现。

史上最详尽 Java 8 集合类 HashMap : 底层实现和原理学习笔记（源码解析）

在Jdk1.8中HashMap的实现方式做了一些改变，但是基本思想还是没有变得，只是在一些地方做了优化，下面来看一下这些改变的地方,数据结构的存储由数组+链表的方式，变化为数组+链表+红黑树的存储方式，当链表长度超过阈值（8）时，将链表转换为红黑树。在性能上进一步得到提升。

史上最详尽 Java 8 集合类 HashMap : 底层实现和原理学习笔记（源码解析）

2、put方法简单解析：

public V put(K key, V value) {
    //调用putVal()方法完成
    return putVal(hash(key), key, value, false, true);
}

final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
               boolean evict) {
    Node<K,V>[] tab; Node<K,V> p; int n, i;
    //判断table是否初始化，否则初始化操作

if ((tab = table) == null || (n = tab.length) == 0

// 其中,Node<K,V>[] resize() , initializes or doubles table size.

n = (tab = resize()).length;

// 计算存储的索引位置，如果没有元素，直接新增节点赋值

if ((p = tab[i = (n - 1) & hash]) == null

)

= newNode(hash, key, value, null

);

else

{

<K,V>

e; K k;

// 节点若已经存在，执行赋值操作

if (p.hash == hash &&
= p.key) == key || (key != null &&

key.equals(k))))

// 判断链表是否是红黑树

else if (p instanceof

TreeNode)

// 红黑树对象操作

e = ((TreeNode<K,V>)p).putTreeVal( this

, tab, hash, key, value);

else

{

// 为链表，

for ( int binCount = 0; ; ++

binCount) {

if ((e = p.next) == null

) {

= newNode(hash, key, value, null

);

// 链表长度8，将链表转化为红黑树存储

if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st

treeifyBin(tab, hash);

break

;

}

// key存在，直接覆盖

if (e.hash == hash &&
= e.key) == key || (key != null &&

key.equals(k))))

break

;

}

if (e != null ) { // existing mapping for key

V oldValue =

e.value;

if (!onlyIfAbsent || oldValue == null

)

value;

afterNodeAccess(e);

return

oldValue;

}

// 记录修改次数

modCount;

// 判断是否需要扩容

if (++size >

threshold)

resize();

// 空操作

afterNodeInsertion(evict);

return null

;

}

如果存在key节点，返回旧值，如果不存在则返回Null。

put方法的代码中有几个关键的方法，分别是：

hash():哈希函数，计算key对应的位置
resize():扩容
putTreeVal():插入红黑树的节点
treeifyBin():树形化容器

前面两个是HashMap的桶链表操作的核心方法，后面的方法是JDK 8之后有关红黑树的操作.

逻辑如下：

先调用 hash() 方法计算哈希值
然后调用 putVal() 方法中根据哈希值进行相关操作
如果当前哈希表内容为空，做扩容
如果要插入的桶中没有元素，新建个节点并放进去
否则从要插入的桶中第一个元素开始查找（这里为什么是第一个元素，下面会讲到）
如果没有碰撞，赋值给e，结束查找
有碰撞，而且当前采用的还是红黑树的节点，调用 putTreeVal() 进行插入
链表节点的话从传统的链表数组中查找、找到赋值给e，结束
如果链表长度达到8，转换成红黑树
最后检查是否需要扩容

[https://blog.csdn.net/yeyazhishang/article/details/83114658 ]

其中, 红黑树中添加一个节点的方法如下:

/**

* Tree version of putVal.

final TreeNode<K,V> putTreeVal(HashMap<K,V> map, Node<K,V>[] tab,

int h, K k, V v) {}

static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root,

TreeNode<K,V> x) {

x.red = true;

for (TreeNode<K,V> xp, xpp, xppl, xppr;;) {

if ((xp = x.parent) == null) {

x.red = false;

return x;

}

else if (!xp.red || (xpp = xp.parent) == null)

return root;

if (xp == (xppl = xpp.left)) {

if ((xppr = xpp.right) != null && xppr.red) {

xppr.red = false;

xp.red = false;

xpp.red = true;

x = xpp;

}

else {

if (x == xp.right) {

root = rotateLeft(root, x = xp);

xpp = (xp = x.parent) == null ? null : xp.parent;

}

if (xp != null) {

xp.red = false;

if (xpp != null) {

xpp.red = true;

root = rotateRight(root, xpp);

}

else {

if (xppl != null && xppl.red) {

xppl.red = false;

xp.red = false;

xpp.red = true;

x = xpp;

}

else {

if (x == xp.left) {

root = rotateRight(root, x = xp);

xpp = (xp = x.parent) == null ? null : xp.parent;

}

if (xp != null) {

xp.red = false;

if (xpp != null) {

xpp.red = true;

root = rotateLeft(root, xpp);

}

其中, 红黑树的左旋,右旋算法实现的代码如下:

/* ------------------------------------------------------------ */

// Red-black tree methods, all adapted from CLR

static <K,V> TreeNode<K,V> rotateLeft(TreeNode<K,V> root,

TreeNode<K,V> p) {

TreeNode<K,V> r, pp, rl;

if (p != null && (r = p.right) != null) {

if ((rl = p.right = r.left) != null)

rl.parent = p;

if ((pp = r.parent = p.parent) == null)

(root = r).red = false;

else if (pp.left == p)

pp.left = r;

else

pp.right = r;

r.left = p;

p.parent = r;

}

return root;

}

static <K,V> TreeNode<K,V> rotateRight(TreeNode<K,V> root,

TreeNode<K,V> p) {

TreeNode<K,V> l, pp, lr;

if (p != null && (l = p.left) != null) {

if ((lr = p.left = l.right) != null)

lr.parent = p;

if ((pp = l.parent = p.parent) == null)

(root = l).red = false;

else if (pp.right == p)

pp.right = l;

else

pp.left = l;

l.right = p;

p.parent = l;

}

return root;

}

节点查找算法:

/**

* Finds the node starting at root p with the given hash and key.

* The kc argument caches comparableClassFor(key) upon first use

* comparing keys.

final TreeNode<K,V> find(int h, Object k, Class<?> kc) {

TreeNode<K,V> p = this;

do {

int ph, dir; K pk;

TreeNode<K,V> pl = p.left, pr = p.right, q;

if ((ph = p.hash) > h)

p = pl;

else if (ph < h)

p = pr;

else if ((pk = p.key) == k || (k != null && k.equals(pk)))

return p;

else if (pl == null)

p = pr;

else if (pr == null)

p = pl;

else if ((kc != null ||

(kc = comparableClassFor(k)) != null) &&

(dir = compareComparables(kc, k, pk)) != 0)

p = (dir < 0) ? pl : pr;

else if ((q = pr.find(h, k, kc)) != null)

return q;

else

p = pl;

} while (p != null);

return null;

}

还有复杂的节点删除算法:

final Node<K,V> removeNode(int hash, Object key, Object value,

boolean matchValue, boolean movable) {

Node<K,V>[] tab; Node<K,V> p; int n, index;

if ((tab = table) != null && (n = tab.length) > 0 &&

(p = tab[index = (n - 1) & hash]) != null) {

Node<K,V> node = null, e; K k; V v;

if (p.hash == hash &&

((k = p.key) == key || (key != null && key.equals(k))))

node = p;

else if ((e = p.next) != null) {

if (p instanceof TreeNode)

node = ((TreeNode<K,V>)p).getTreeNode(hash, key);

else {

do {

if (e.hash == hash &&

((k = e.key) == key ||

(key != null && key.equals(k)))) {

node = e;

break;

}

p = e;

} while ((e = e.next) != null);

}

if (node != null && (!matchValue || (v = node.value) == value ||

(value != null && value.equals(v)))) {

if (node instanceof TreeNode)

((TreeNode<K,V>)node).removeTreeNode(this, tab, movable);

else if (node == p)

tab[index] = node.next;

else

p.next = node.next;

++modCount;

--size;

afterNodeRemoval(node);

return node;

}

return null;

}

/**

* Removes the given node, that must be present before this call.

* This is messier than typical red-black deletion code because we

* cannot swap the contents of an interior node with a leaf

* successor that is pinned by "next" pointers that are accessible

* independently during traversal. So instead we swap the tree

* linkages. If the current tree appears to have too few nodes,

* the bin is converted back to a plain bin. (The test triggers

* somewhere between 2 and 6 nodes, depending on tree structure).

final void removeTreeNode(HashMap<K,V> map, Node<K,V>[] tab,

boolean movable) {

int n;

if (tab == null || (n = tab.length) == 0)

return;

int index = (n - 1) & hash;

TreeNode<K,V> first = (TreeNode<K,V>)tab[index], root = first, rl;

TreeNode<K,V> succ = (TreeNode<K,V>)next, pred = prev;

if (pred == null)

tab[index] = first = succ;

else

pred.next = succ;

if (succ != null)

succ.prev = pred;

if (first == null)

return;

if (root.parent != null)

root = root.root();

if (root == null || root.right == null ||

(rl = root.left) == null || rl.left == null) {

tab[index] = first.untreeify(map); // too small

return;

}

TreeNode<K,V> p = this, pl = left, pr = right, replacement;

if (pl != null && pr != null) {

TreeNode<K,V> s = pr, sl;

while ((sl = s.left) != null) // find successor

s = sl;

boolean c = s.red; s.red = p.red; p.red = c; // swap colors

TreeNode<K,V> sr = s.right;

TreeNode<K,V> pp = p.parent;

if (s == pr) { // p was s's direct parent

p.parent = s;

s.right = p;

}

else {

TreeNode<K,V> sp = s.parent;

if ((p.parent = sp) != null) {

if (s == sp.left)

sp.left = p;

else

sp.right = p;

}

if ((s.right = pr) != null)

pr.parent = s;

}

p.left = null;

if ((p.right = sr) != null)

sr.parent = p;

if ((s.left = pl) != null)

pl.parent = s;

if ((s.parent = pp) == null)

root = s;

else if (p == pp.left)

pp.left = s;

else

pp.right = s;

if (sr != null)

replacement = sr;

else

replacement = p;

}

else if (pl != null)

replacement = pl;

else if (pr != null)

replacement = pr;

else

replacement = p;

if (replacement != p) {

TreeNode<K,V> pp = replacement.parent = p.parent;

if (pp == null)

root = replacement;

else if (p == pp.left)

pp.left = replacement;

else

pp.right = replacement;

p.left = p.right = p.parent = null;

}

TreeNode<K,V> r = p.red ? root : balanceDeletion(root, replacement);

if (replacement == p) { // detach

TreeNode<K,V> pp = p.parent;

p.parent = null;

if (pp != null) {

if (p == pp.left)

pp.left = null;

else if (p == pp.right)

pp.right = null;

}

if (movable)

moveRootToFront(tab, r);

}

static <K,V> TreeNode<K,V> balanceDeletion(TreeNode<K,V> root,

TreeNode<K,V> x) {

for (TreeNode<K,V> xp, xpl, xpr;;) {

if (x == null || x == root)

return root;

else if ((xp = x.parent) == null) {

x.red = false;

return x;

}

else if (x.red) {

x.red = false;

return root;

}

else if ((xpl = xp.left) == x) {

if ((xpr = xp.right) != null && xpr.red) {

xpr.red = false;

xp.red = true;

root = rotateLeft(root, xp);

xpr = (xp = x.parent) == null ? null : xp.right;

}

if (xpr == null)

x = xp;

else {

TreeNode<K,V> sl = xpr.left, sr = xpr.right;

if ((sr == null || !sr.red) &&

(sl == null || !sl.red)) {

xpr.red = true;

x = xp;

}

else {

if (sr == null || !sr.red) {

if (sl != null)

sl.red = false;

xpr.red = true;

root = rotateRight(root, xpr);

xpr = (xp = x.parent) == null ?

null : xp.right;

}

if (xpr != null) {

xpr.red = (xp == null) ? false : xp.red;

if ((sr = xpr.right) != null)

sr.red = false;

}

if (xp != null) {

xp.red = false;

root = rotateLeft(root, xp);

}

x = root;

}

else { // symmetric

if (xpl != null && xpl.red) {

xpl.red = false;

xp.red = true;

root = rotateRight(root, xp);

xpl = (xp = x.parent) == null ? null : xp.left;

}

if (xpl == null)

x = xp;

else {

TreeNode<K,V> sl = xpl.left, sr = xpl.right;

if ((sl == null || !sl.red) &&

(sr == null || !sr.red)) {

xpl.red = true;

x = xp;

}

else {

if (sl == null || !sl.red) {

if (sr != null)

sr.red = false;

xpl.red = true;

root = rotateLeft(root, xpl);

xpl = (xp = x.parent) == null ?

null : xp.left;

}

if (xpl != null) {

xpl.red = (xp == null) ? false : xp.red;

if ((sl = xpl.left) != null)

sl.red = false;

}

if (xp != null) {

xp.red = false;

root = rotateRight(root, xp);

}

x = root;

}

/**

* Ensures that the given root is the first node of its bin.

static <K,V> void moveRootToFront(Node<K,V>[] tab, TreeNode<K,V> root) {

int n;

if (root != null && tab != null && (n = tab.length) > 0) {

int index = (n - 1) & root.hash;

TreeNode<K,V> first = (TreeNode<K,V>)tab[index];

if (root != first) {

Node<K,V> rn;

tab[index] = root;

TreeNode<K,V> rp = root.prev;

if ((rn = root.next) != null)

((TreeNode<K,V>)rn).prev = rp;

if (rp != null)

rp.next = rn;

if (first != null)

first.prev = root;

root.next = first;

root.prev = null;

}

assert checkInvariants(root);

}

JDK 7 以前，当HashMap中某个桶的结构为链表时，遍历的时间复杂度为O(n)，JDK 8之后，桶中过多元素的话会转换成了红黑树，这时候的遍历时间复杂度就是O(logn)。

hash() 函数原理分析

在Java 8 之前，HashMap和其他基于map的类都是通过链地址法解决冲突，它们使用单向链表来存储相同索引值的元素。在最坏的情况下，这种方式会将HashMap的get方法的性能从O(1)降低到O(n)。为了解决在频繁冲突时hashmap性能降低的问题，Java 8中使用平衡树来替代链表存储冲突的元素。这意味着我们可以将最坏情况下的性能从O(n)提高到O(logn)。

在Java 8中使用常量TREEIFY_THRESHOLD来控制是否切换到平衡树来存储。目前，这个常量值是8，这意味着当有超过8个元素的索引一样时，HashMap会使用树来存储它们。

这一改变是为了继续优化常用类。大家可能还记得在Java 7中为了优化常用类对ArrayList和HashMap采用了延迟加载的机制，在有元素加入之前不会分配内存，这会减少空的链表和HashMap占用的内存。

这一动态的特性使得HashMap一开始使用链表，并在冲突的元素数量超过指定值时用平衡二叉树替换链表。不过这一特性在所有基于hash table的类中并没有，例如Hashtable和WeakHashMap。

目前，只有ConcurrentHashMap,LinkedHashMap和HashMap会在频繁冲突的情况下使用平衡树。

什么时候会产生冲突

HashMap中调用hashCode()方法来计算hashCode。

由于在Java中两个不同的对象可能有一样的hashCode,所以不同的键可能有一样hashCode，从而导致冲突的产生。

从JDK 8开始，HashMap，LinkedHashMap和ConcurrentHashMap为了提升性能，在频繁冲突的时候使用平衡树来替代链表。因为HashSet内部使用了HashMap，LinkedHashSet内部使用了LinkedHashMap，所以他们的性能也会得到提升。

HashMap的快速高效，使其使用非常广泛。其原理是，调用hashCode（）和equals（）方法，并对hashcode进行一定的哈希运算得到相应value的位置信息，将其分到不同的桶里。桶的数量一般会比所承载的实际键值对多。当通过key进行查找的时候，往往能够在常数时间内找到该value。

但是，当某种针对key的hashcode的哈希运算得到的位置信息重复了之后，就发生了哈希碰撞。这会对HashMap的性能产生灾难性的影响。

在Java 8 之前，如果发生碰撞往往是将该value直接链接到该位置的其他所有value的末尾，即相互碰撞的所有value形成一个链表。

因此，在最坏情况下，HashMap的查找时间复杂度将退化到O（n）.

但是在Java 8 中，该碰撞后的处理进行了改进。当一个位置所在的冲突过多时，存储的value将形成一个排序二叉树，排序依据为key的hashcode。

则在最坏情况下，HashMap的查找时间复杂度将从O（1）退化到O（logn）。

虽然是一个小小的改进，但意义重大：

1、O（n）到O（logn）的时间开销。

2、如果恶意程序知道我们用的是Hash算法，则在纯链表情况下，它能够发送大量请求导致哈希碰撞，然后不停访问这些key导致HashMap忙于进行线性查找，最终陷入瘫痪，即形成了拒绝服务攻击（DoS）。

[ https://blog.csdn.net/u014590757/article/details/79575101 ]

/**

* Computes key.hashCode() and spreads (XORs) higher bits of hash

* to lower. Because the table uses power-of-two masking, sets of

* hashes that vary only in bits above the current mask will

* always collide. (Among known examples are sets of Float keys

* holding consecutive whole numbers in small tables.) So we

* apply a transform that spreads the impact of higher bits

* downward. There is a tradeoff between speed, utility, and

* quality of bit-spreading. Because many common sets of hashes

* are already reasonably distributed (so don't benefit from

* spreading), and because we use trees to handle large sets of

* collisions in bins, we just XOR some shifted bits in the

* cheapest possible way to reduce systematic lossage, as well as

* to incorporate impact of the highest bits that would otherwise

* never be used in index calculations because of table bounds.

static final int hash(Object key) {

int h;

return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);

}

代码说明:

如果Key值为null，返回0；如果Key值不为空，返回原hash值和原hash值无符号右移16位的值按位异或的结果。

我们知道，按位异或就是把两个数按二进制，相同就取0，不同就取1。

比如：0101 ^ 1110 的结果为 1011。（记得以前上数字电路课的时候学过）异或的速度是非常快的。

[ https://blog.csdn.net/anxpp/article/details/51234835 ]

1、如果key为空，那么hash值置为0。HashMap允许null作为键，虽然这样，因为null的hash值一定是0，而且null==null为真，所以HashMap里面最多只会有一个null键。而且这个null键一定是放在数组的第一个位置上。但是如果存在hash碰撞，该位置上形成链表了，那么null键对应的节点就不确定在链表中的哪个位置了（取决于插入顺序，并且每次扩容其在链表中的位置都可能会改变）。

2、如果key是个不为空的对象，那么将key的hashCode值h和h无符号右移16位后的值做异或运算，得到最终的hash值。

从代码中目前我们可确定的信息是：hashCode值（h）是计算基础，在h的基础上进行了两次位运算（无符号右移、异或）

虽然经过hash算法之后与直接使用hashCode的输出不同，但是数组下标还是出现了碰撞的情况（会有相同的下标出现）。所以hash方法也不能解决碰撞的问题（实际上碰撞不算是问题，我们只是想尽可能的少发生）。那么为什么不直接用hashCode而非要经过这么一种位运算来产生一个hash值呢?

为什么【0-65535】范围内的数值h

h ^ (h >>> 16) = h ？

从例子中的二进制的运算描述我们可以发现，【0-65535】范围内的数值的二进制的高16位都是0，在进行无符号右移16位后，原来的高16位变成了现在的低16位，现在的高16位补了16个0，这种操作之后当前值就是32个0，以32个0去和任何整数值N做异或运算结果都还是N。而不再【0-65535】范围内的数值的高16位都包含有1数字位，在无符号右移16位后，虽然高位仍然补了16个0，但是当前的低位任然包含有1数字位，所以最终的运算结果会发生变化。

hash方法并不能杜绝碰撞。

"name".hashCode(): 3373707

hash("name"): 3373752

"sex".hashCode() : 113766

hash("sex"): 113767

"level".hashCode() : 102865796

hash("level"): 102866341

"phone".hashCode(): 106642798

hash("phone"): 106642229

而且通过对比观察，hash后的值和hashCode值虽然不尽相同，而对于正数的hashCode的产生的hash值即便和原值不同，差别也不是很大。为什么不直接使用hashCode作为hash值呢？为什么非要经过 h ^ (h >>> 16) 这一步运算呢？

看注释.

寻址计算时，能够参与到计算的有效二进制位仅仅是右侧和数组长度值对应的那几位，意味着发生碰撞的几率会高。

通过移位和异或运算让hashCode的高位能够参与到寻址计算中。

采用这种方式是为了在性能、实用性、分布质量上取得一个平衡。

有很多hashCode算法都已经是分布合理的了，并且大量碰撞时，还可以通过树结构来解决查询性能问题。

所以用了性能比较高的位运算来让高位参与到寻址运算中，位运算对于系统损耗相对低廉。

[https://blog.csdn.net/weixin_42340670/article/details/80574965]

我们知道hashMap中的桶位都是以 oldCap<<1（即原容量*2）来增长的，所以最终这个hash值要存放的时候，都是跟一连串二进制的“1"作与运算的，而容量定义为int类型，java中int类型为4字节，即32位，但是Integer.MAX为0x7fffffff，也就是2^31 - 1 那么大（因为最高位被用作符号位），故取16计算; 另一个原因，跟对象本身的hash值（为int）有关。

一：hashMap的工作原理

HashMap是基于链地址法的原理，使用put(key, value)存储对象到HashMap中，使用get(key)从HashMap中获取对象。

当我们给put()方法传递键和值时，我们先对键调用hashCode()方法计算hash从而得到bucket位置，进一步存储，HashMap会根据当前bucket的占用情况自动调整容量(超过Load Facotr则resize为原来的2倍)，储存Node对象。

使用get(key)从HashMap中获取对象时，它调用hashCode计算hash从而得到bucket位置，并进一步调用equals()方法确定键值对。如果发生碰撞的时候，Hashmap通过链表将产生碰撞冲突的元素组织起来，在Java 8中，如果一个bucket中碰撞冲突的元素超过某个限制(默认是8)，则使用红黑树来替换链表，从而提高速度。

二：hash冲突

如果两个不同对象的hashCode相同，这种现象称为hash冲突。

三：hash冲突的解决办法

在hashMap中，采用链地址法解决hash冲突。

常用方法有：开发定址法、再哈希法、链地址法、建立公共溢出区。

（1）开放定址法

这种方法也称再散列法，其基本思想是：当关键字key的哈希地址p=H（key）出现冲突时，以p为基础，产生另一个哈希地址p1，如果p1仍然冲突，再以p为基础，产生另一个哈希地址p2，…，直到找出一个不冲突的哈希地址pi ，将相应元素存入其中。这种方法有一个通用的再散列函数形式：

Hi=（H（key）+di）% m i=1，2，…，n

其中H（key）为哈希函数，m 为表长，di称为增量序列。增量序列的取值方式不同，相应的再散列方式也不同。主要有以下三种：

1）线性探测再散列

dii=1，2，3，…，m-1

这种方法的特点是：冲突发生时，顺序查看表中下一单元，直到找出一个空单元或查遍全表。

2）二次探测再散列

di=12，-12，22，-22，…，k2，-k2 ( k<=m/2 )

这种方法的特点是：冲突发生时，在表的左右进行跳跃式探测，比较灵活。

3）伪随机探测再散列

di=伪随机数序列。

具体实现时，应建立一个伪随机数发生器，（如i=(i+p) % m），并给定一个随机数做起点。

例如，已知哈希表长度m=11，哈希函数为：H（key）= key % 11，则H（47）=3，H（26）=4，H（60）=5，假设下一个关键字为69，则H（69）=3，与47冲突。

如果用线性探测再散列处理冲突，下一个哈希地址为H1=（3 + 1）% 11 = 4，仍然冲突，再找下一个哈希地址为H2=（3 + 2）% 11 = 5，还是冲突，继续找下一个哈希地址为H3=（3 + 3）% 11 = 6，此时不再冲突，将69填入5号单元。

如果用二次探测再散列处理冲突，下一个哈希地址为H1=（3 + 12）% 11 = 4，仍然冲突，再找下一个哈希地址为H2=（3 - 12）% 11 = 2，此时不再冲突，将69填入2号单元。

如果用伪随机探测再散列处理冲突，且伪随机数序列为：2，5，9，……..，则下一个哈希地址为H1=（3 + 2）% 11 = 5，仍然冲突，再找下一个哈希地址为H2=（3 + 5）% 11 = 8，此时不再冲突，将69填入8号单元。

（2）再哈希法

这种方法是同时构造多个不同的哈希函数：

Hi=RH1（key） i=1，2，…，k

当哈希地址Hi=RH1（key）发生冲突时，再计算Hi=RH2（key）……，直到冲突不再产生。这种方法不易产生聚集，但增加了计算时间。

（3）链地址法

这种方法的基本思想是将所有哈希地址为i的元素构成一个称为同义词链的单链表，并将单链表的头指针存在哈希表的第i个单元中，因而查找、插入和删除主要在同义词链中进行。链地址法适用于经常进行插入和删除的情况。

（4）建立公共溢出区

这种方法的基本思想是：将哈希表分为基本表和溢出表两部分，凡是和基本表发生冲突的元素，一律填入溢出表。

[https://blog.csdn.net/WoAiBianCheng123abc/article/details/82931800]

转成红黑树的阈值

开始转成红黑树的阈值(TREEIFY_THRESHOLD)为什么是 8 ?

/**
 * Because TreeNodes are about twice the size of regular nodes, we
 * use them only when bins contain enough nodes to warrant use
 * (see TREEIFY_THRESHOLD). And when they become too small (due to
 * removal or resizing) they are converted back to plain bins.In
 * usages with well-distributed user hashCodes, tree bins are
 * rarely used.  Ideally, under random hashCodes, the frequency of
 * nodes in bins follows a Poisson distribution
 * (http://en.wikipedia.org/wiki/Poisson_distribution) with a
 * parameter of about 0.5 on average for the default resizing
 * threshold of 0.75, although with a large variance because of
 * resizing granularity. Ignoring variance, the expected
 * occurrences of list size k are (exp(-0.5) * pow(0.5, k) /
 * factorial(k)). The first values are:
 *
 * 0:    0.60653066
 * 1:    0.30326533
 * 2:    0.07581633
 * 3:    0.01263606
 * 4:    0.00157952
 * 5:    0.00015795
 * 6:    0.00001316
 * 7:    0.00000094
 * 8:    0.00000006
 * more: less than 1 in ten million
 **/

红黑树

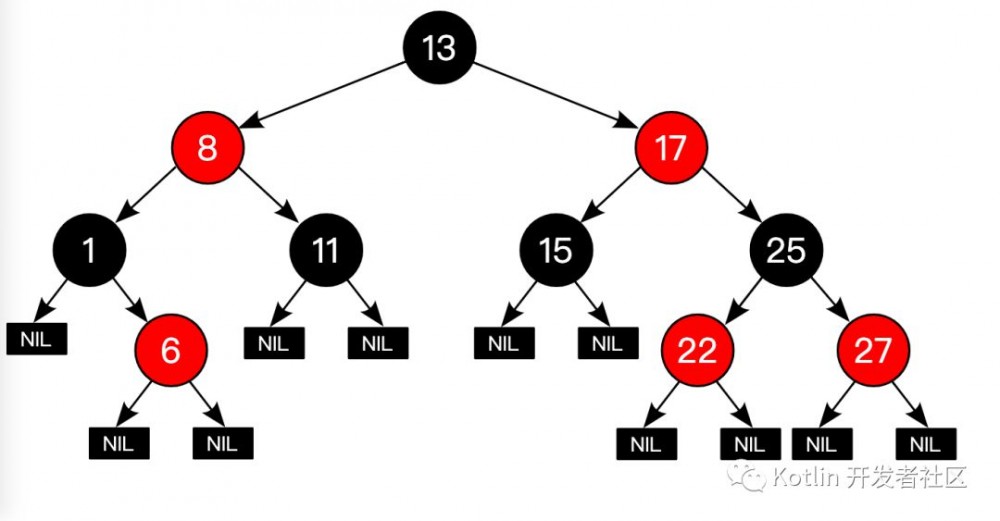
史上最详尽 Java 8 集合类 HashMap : 底层实现和原理学习笔记（源码解析）

[https://zh.wikipedia.org/wiki/%E7%BA%A2%E9%BB%91%E6%A0%91]

红黑树（英语： Red–black tree ）是一种自平衡二叉查找树，是在计算机科学中用到的一种数据结构，典型的用途是实现关联数组。它在1972年由鲁道夫·贝尔发明，被称为" 对称二叉B树 "，它现代的名字源于Leo J. Guibas和 Robert Sedgewick 于 1978年写的一篇论文。红黑树的结构复杂，但它的操作有着良好的最坏情况运行时间，并且在实践中高效：它可以O(log n) 时间内完成查找，插入和删除，这里的 n 是树中元素的数目。

红黑树是每个节点都带有颜色属性的二叉查找树，颜色为红色或黑色。在二叉查找树强制一般要求以外，对于任何有效的红黑树我们增加了如下的额外要求：

节点是红色或黑色。
根是黑色。
所有叶子都是黑色（叶子是NIL节点）。
每个红色节点必须有两个黑色的子节点。（从每个叶子到根的所有路径上不能有两个连续的红色节点。）
从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。

这些约束确保了红黑树的关键特性：从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果是这个树大致上是平衡的。因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例，这个在高度上的理论上限允许红黑树在最坏情况下都是高效的，而不同于普通的二叉查找树。

要知道为什么这些性质确保了这个结果，注意到性质4导致了路径不能有两个毗连的红色节点就足够了。最短的可能路径都是黑色节点，最长的可能路径有交替的红色和黑色节点。因为根据性质5所有最长的路径都有相同数目的黑色节点，这就表明了没有路径能多于任何其他路径的两倍长。

红黑树的操作示例图 :

https://www.cs.auckland.ac.nz/software/AlgAnim/red_black_op.html

Red-Black Tree Operation

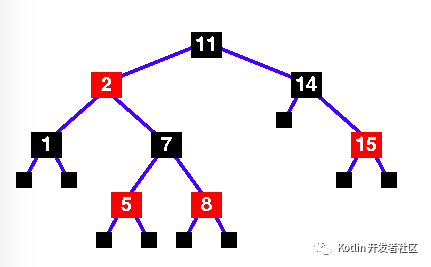
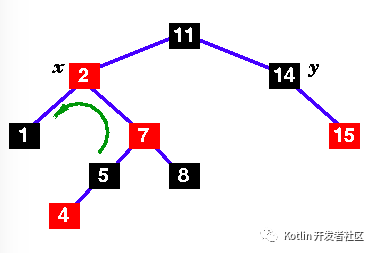
Here's an example of insertion into a red-black tree (taken from Cormen, p269).

	1.Here's the original tree .. Note that in the following diagrams, the black sentinel nodes have been omitted to keep the diagrams simple.
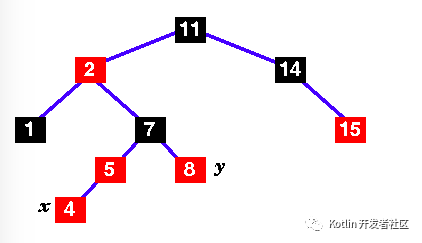
	This is no longer a red-black tree - there are two successive red nodes on the path 11 - 2 - 7 - 5 - 4 Mark the new node, x, and it's uncle , y. y is red, so we have case 1 ...
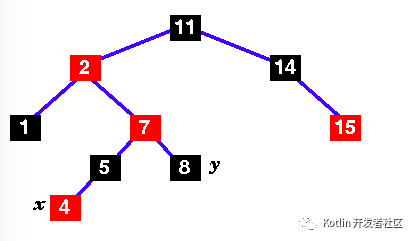
	3.Change the colours of nodes 5, 7 and 8.
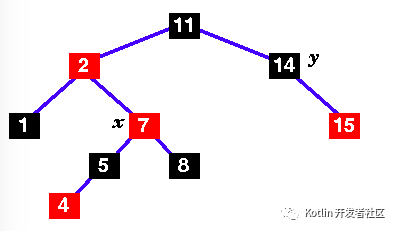
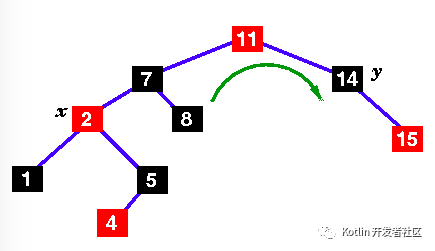
	x's parent (2) is still red, so this isn't a red-black tree yet. Mark the uncle, y. In this case, the uncle is black, so we have case 2 ...
	5.Move x up and rotate left.
	6.Still not a red-black tree .. the uncle is black, but x's parent is to the left ..
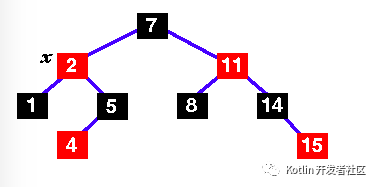
	7.Change the colours of 7 and 11 and rotate right ..
	This is now a red-black tree, so we're finished! O( log n) time!