转载

剑指Offer题目11：实现函数double Power（double base, int exponent），求base的exponent次方。（...

面试题11：给定一个double类型的浮点数base和int类型的整数exponent。求base的exponent次方。

解题思路

思路1：brute force 累乘法，时间复杂度O(n)

挨个乘，exponent 为 n，则累乘 n 次得出结果。

思路2：使用递归，时间复杂度O(logn)

当n为偶数，a^n =（a^n/2）*（a^n/2）

当n为奇数，a^n = a^[(n-1)/2] * a^[(n-1)/2] * a

思路3：同递归的思路，但采用循环法（递归和循环都是可以互换的）

复制代码

代码实现

brute force 累乘法

public double Power(double base, int exponent) {
        if(base == 0) {
            return 0;
        }
        double result = 1.0;
        int positiveExponent = Math.abs(exponent);
        for(int i=1; i<=positiveExponent; i++) {
            result *= base;
        }
        return exponent < 0 ? 1/result : result;
  }
复制代码

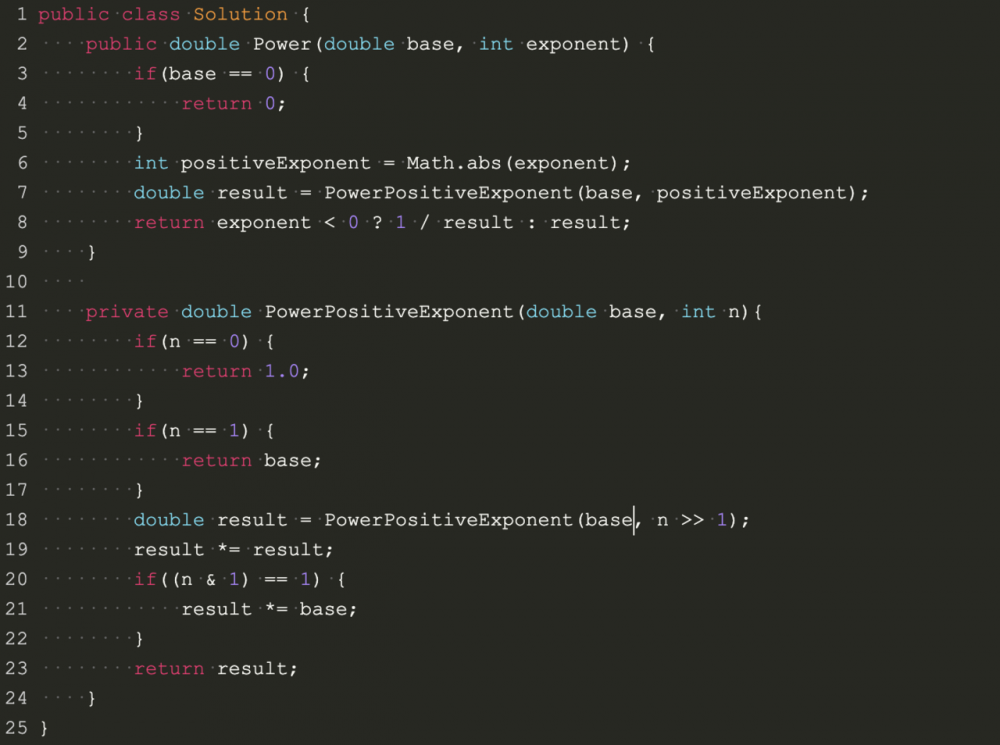
剑指Offer题目11：实现函数double Power（double base, int exponent），求base的exponent次方。（...

递归法

public class Solution {
    public double Power(double base, int exponent) {
        if(base == 0) {
            return 0;
        }
        int positiveExponent = Math.abs(exponent);
        double result = PowerPositiveExponent(base, positiveExponent);
        return exponent < 0 ? 1 / result : result;
    }
    
    private double PowerPositiveExponent(double base, int n){
        if(n == 0) {
            return 1.0;
        }
        if(n == 1) {
            return base;
        }
        double result = PowerPositiveExponent(base, n >> 1);
        result *= result;
        if((n & 1) == 1) {
            result *= base;
        }
        return result;
    }
}
复制代码

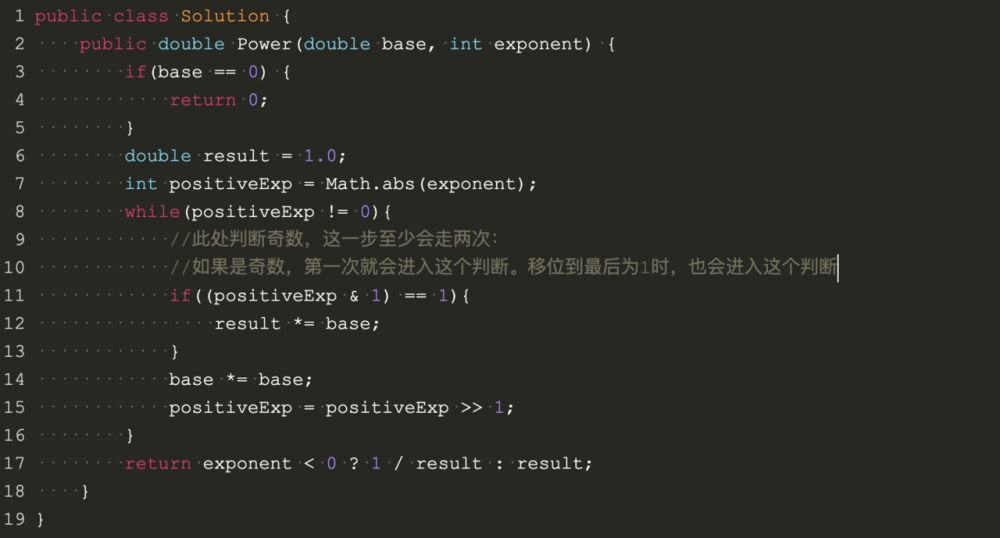
循环法

public class Solution {
    public double Power(double base, int exponent) {
        if(base == 0) {
            return 0;
        }
        double result = 1.0;
        int positiveExp = Math.abs(exponent);
        while(positiveExp != 0){
            //此处判断奇数，这一步至少会走两次：
            //如果是奇数，第一次就会进入这个判断。移位到最后为1时，也会进入这个判断
            if((positiveExp & 1) == 1){
                result *= base;
            }
            base *= base;
            positiveExp = positiveExp >> 1;
        }
        return exponent < 0 ? 1 / result : result;
    }
}
复制代码