图解二叉树和二分搜索树（Java代码实现）
同步于 github.com/fish-stack/…
其实我觉得所有的数据结构都是开始时人为的给它规定一些规则，然后如果一个数据结构满足这些规则，那么我们就可以推导出一些特殊的性质，然后再通过这些性质来实现一些算法。
所以我认为学习一个数据结构基本的套路就是：
-
假设了这个数据结构满足哪些规则？
-
利用这些规则能够推导出什么性质？
-
如何利用这些性质进行增删改查？
利用之前的性质，一般能提高我们的查询效率。但是为了维护数据结构满足之前规则，我们在添加和删除时往往需要付出一些额外的代价。
然后我们还要考虑这些操作的时间复杂度，将它用于某些特定算法。
接下来我就按照上面的套路来说说二叉树和二分搜索树。
二叉树
什么是二叉搜索树？
或者说二叉树有哪些规则？
- 由一个个节点组成，每个节点最多有两个子节点
- 有且只有一个根节点
大体来说，一个二叉树长这样的：
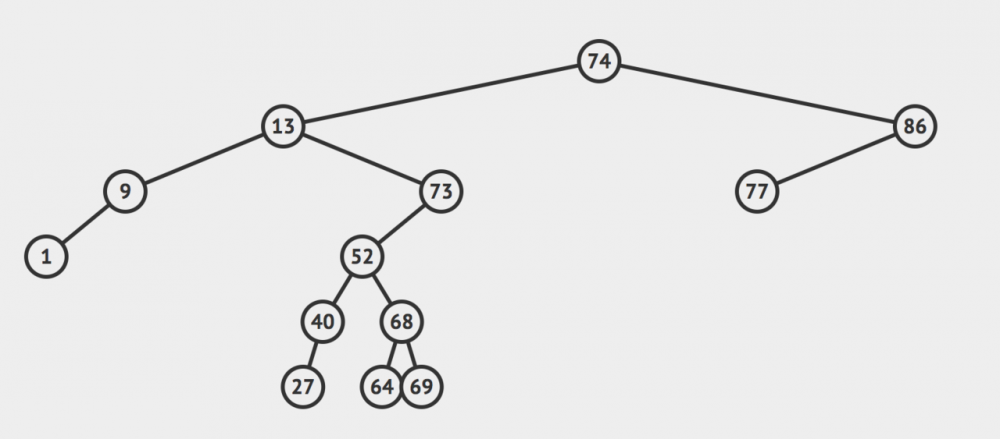
然后其中的每个节点用Java代码描述的话大致长这样的:
class Node<E>{
E e;
Node left;
Node right;
}
复制代码
其中E是一个泛型，用来表示我们的节点存储的元素的类型；然后我们用e这个字段来存储元素。其中left和right用来存储我们的左右两个子节点。
注意的是：
- 一个值为null的变量也可以看做是二叉树
- 一个链表可以看做是特殊的二叉树
- 一个二叉树可能很“平均”，每个节点的左边的所有节点的数量和右边的所有节点的数量一样多；也可能和畸形，像链表一样。
二叉树的性质
通过上面的规则，我们能够推导树二叉树有哪些性质呢？
很显然，二叉树是一个天然的递归结构。我们可以看到，二叉树的每一个子节点也是一个二叉树。 然后二叉树也没有什么其他特殊的性质了，主要给的规则太模糊。一般来说，一个数据结构的限制越多，越能推导出一些有用的性质；同时在插入和删除时，需要更多的代价来维护它的特性。
查询和删除
对于二叉树的查询和增删的复杂度是不确定的。主要是在上面的条件下，这个数据结构太随意了，长什么样都有可能，没有固定的查询和增删的复杂度。
相关算法
也没有什么专门的算法，顶多就是可以利用它的递归性质做一点文章。我们后续的算法会用到很多的递归。
所以下面我们重点说一说二分搜索树。
二分搜索树
什么是二分搜索树？
首先它是一颗二叉树，满足上面所说的规则和性质。
然后人们为它额外制定了这个规则：
二分搜索树中，对于每一个节点：它的值大于左子树任意一个节点的值，并且小于其右子树任意一个节点的值。
这句话包含的信息很多哦，下面的我们来分析下
二分搜索树的性质
二分搜索树大致长这样的：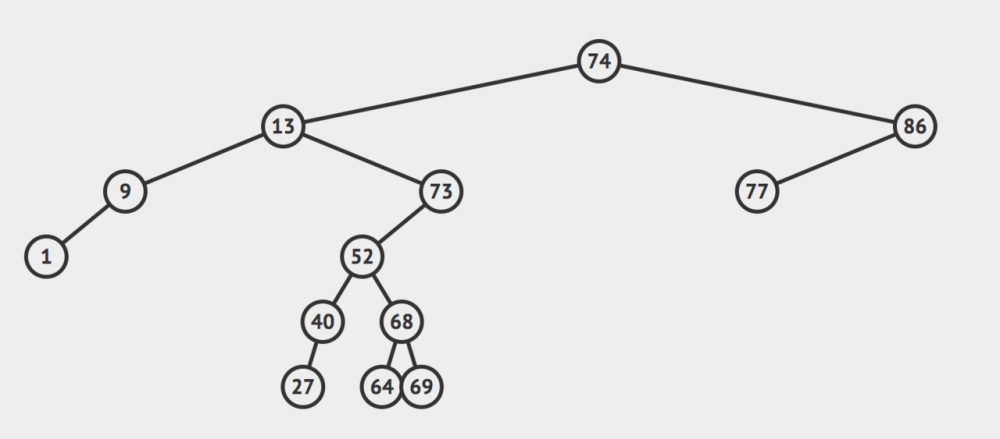 
就是我们之前见过的那颗二叉树。
也可以是这样的：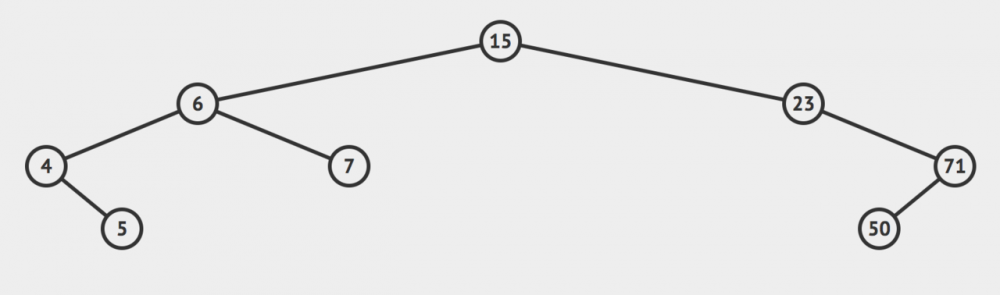 
总之，满足上面这个规则的二叉树就是一个二分搜索树。
制定这样的规则有什么好处呢？或者说我们通过上面的规则可以推导出哪些性质呢？
很明显，对于二分搜索树我们可以使用二分查找法。假设我们要在一颗二分搜索树中查询某一个值是否存在，那么我们只需要从根节点开始：
- 如果根节点的值就是我们要寻找的值，那么直接返回true就行了
- 如果根节点的子比我们的目标节点的值大，我们就递归的向左子树查找；
- 如果根节点的子比我们的目标节点的值小，我们就递归的向右子树查找。
唉，大家注意了，我在上面的描述中用了递归的概念。
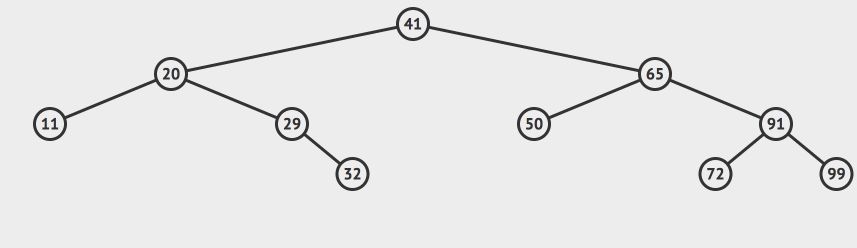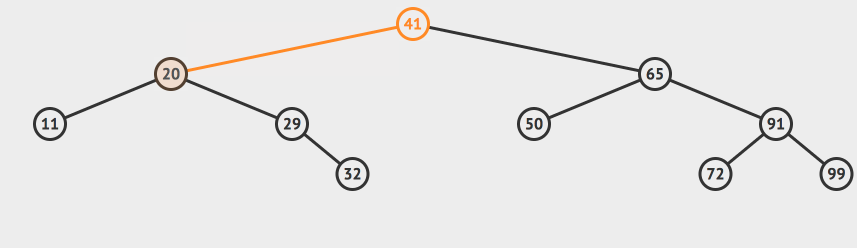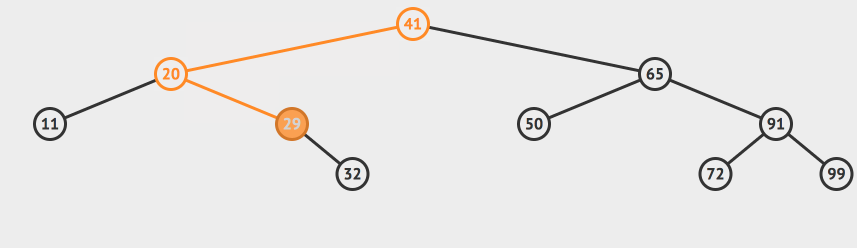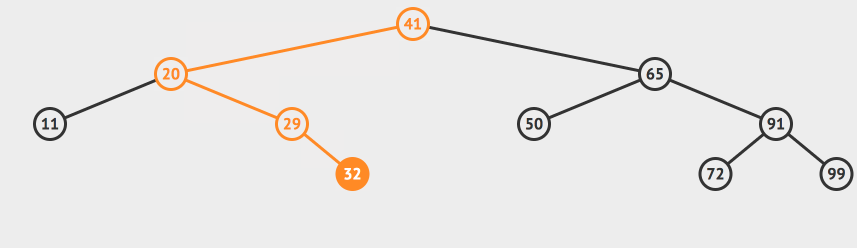
我们用个动画来演示下：
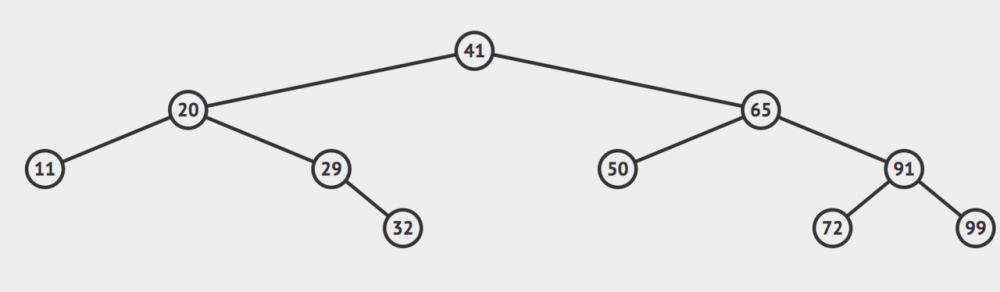一开始我们有这样的一颗树，假设我们希望在这个二分搜索树中查找值为32的节点是否存在。
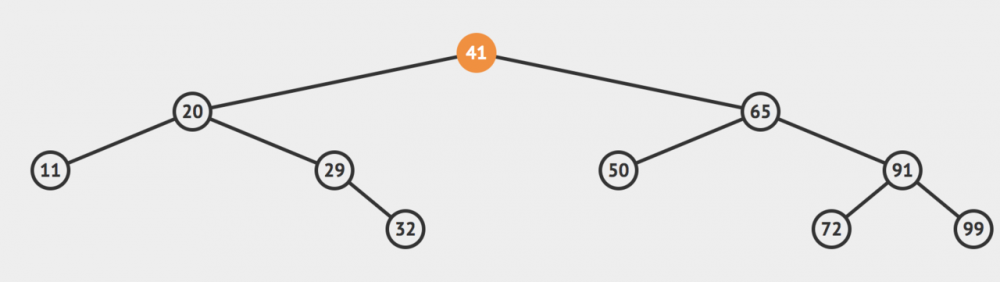我们可以首先查看根节点，发现根节点的值是41，大于我们的目标值，那么我们就可以根据二分搜索树的性质直接排除掉根节点右侧的所有的节点，目标值只有可能存在于根节点的左侧。
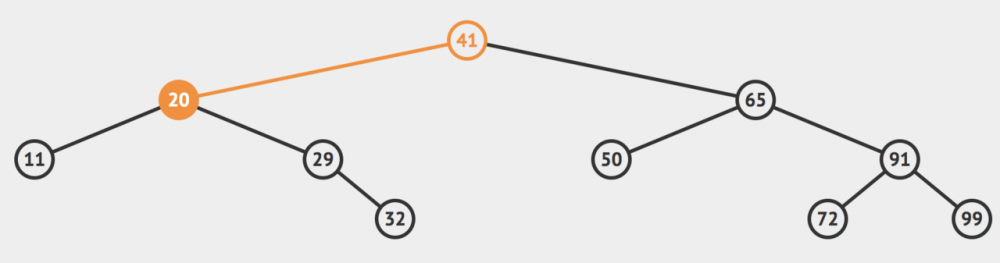然后我们来到41的左节点，也就是20这个节点。我们发现这个节点的值小于32，所有目标值只有可能存在于20的右边。于是我们来到的29这个节点。
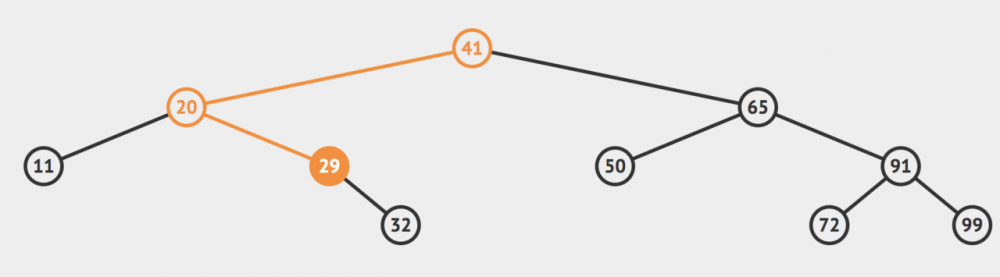同理我们递归的对29这个节点完成上面的操作，来到了32这个节点
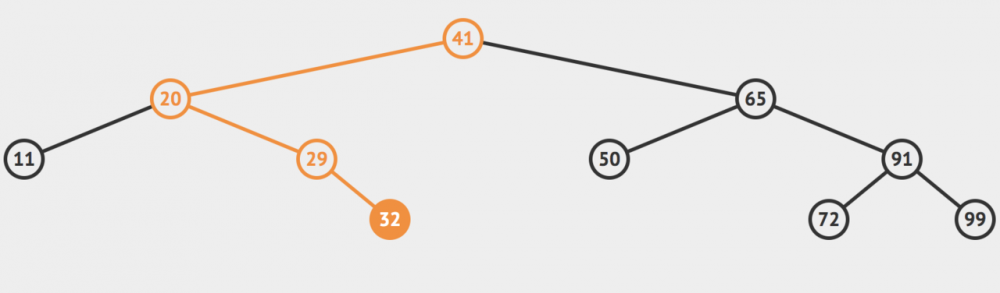
发现这个节点就是我们的目标值，直接返回true。当然，如果没找到话，就返回false。
把上述的过程用动画来演示，就是这样的：
其实，二分搜索树的核心竞争力就是能够使用二分查找法来查询元素。
那么下面我们来好好分析下它相关的时间复杂度。
查询元素
我们知道，如果对一个有序的数组来使用二分搜索法，它的时间复杂度是O(logN)。
我们的二分搜索树看起来也是O(logN)的，但是对于我们的二分搜索树来说，有一个非常严重的问题：它不一定是平衡的。
比如说对于这样的二分搜索树：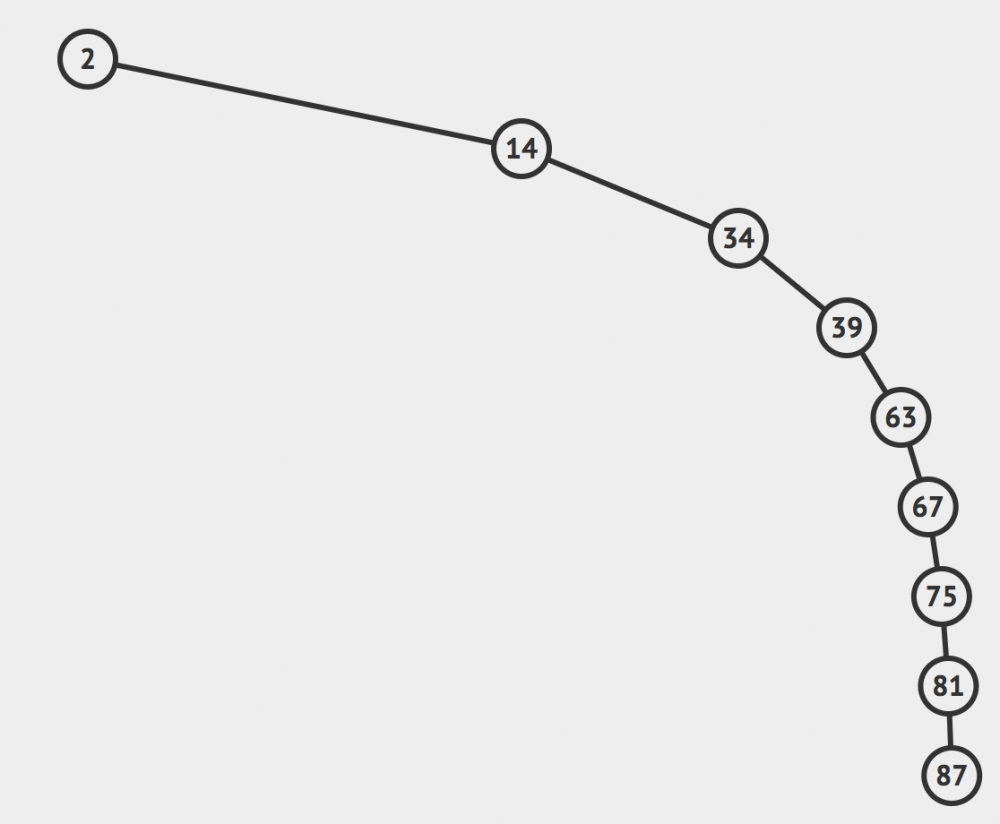 
其实它已经退化成了一个链表了，查询它的元素的时间复杂度和链表一样，都是O(N).
假设这颗树的高度是h，那么查询其中的元素的时间复杂度的具体的值就是O(logh)，而h的取值在logN到N之间。
具体来说，h的值取决于它是否是平衡的，如果是完全平衡的，h的值就是logN；如果退化成链表，那么h的值就是N。目前的情况就是看运气。
为什么说看运气呢？因为对于同样的元素的集合，插入顺序的不同，导致它的不同的平衡程度。
比如说我想把1,2,3,4,5,6,7,8,9插入到一个二分搜索树中。
运气差的话你可能是这样的：
运气好的话你可能是这样的：
后者就是非常平衡的二分搜索树了，你找不到比它更加平衡的了。我们后续会专门的设计一些机制确保它是平衡的。
Java代码
好了，到了这一步我们来用过Java代码来实现一下吧。
下面是代码的基本盘：
import lombok.Getter;
import lombok.ToString;
import java.util.LinkedList;
import java.util.Queue;
/**
* 二分搜索树
* @param <E>
*/
@ToString
public class BSTree<E extends Comparable<E>> {
private Node root;
@Getter
private int size;
public BSTree() {
}
public boolean isEmpty(){
return size == 0;
}
@ToString
private class Node{
public E e;
public Node left, right;
public Node(E e){
this.e = e;
}
}
}
复制代码
这是我们的代码基本盘：
@ToString
然后我们来看看如何查询一个元素，查询的过程我相信我之前的描述以及非常清楚了。具体到Java代码中也非常简单：
/**
* 看看这个节点以及它的子节点是不是包含e
* @param e 要查找的元素
* @param node 目标节点
* @return 当前二分搜索树是否包含目标值
*/
private boolean contains(E e, Node node){
// 这里我们还要注意下node为null的情况
if (node == null) {
return false;
}
// 判断当前节点是否包含目标节点
if (node.e.equals(e)){
// 既然已经查询到了，直接返回即可
return true;
// 判断目标值e可能会出现在当前节点的左边还是右边
} else if (node.e.compareTo(e) > 0) {
// 说明在当前节点的左边，递归查询即可
return contains(e, node.left);
} else {
// 说明在当前节点的右边，递归查询即可
return contains(e, node.right);
}
}
复制代码
我们的代码整体上就是这样写的，用流程图来表示就是这样的：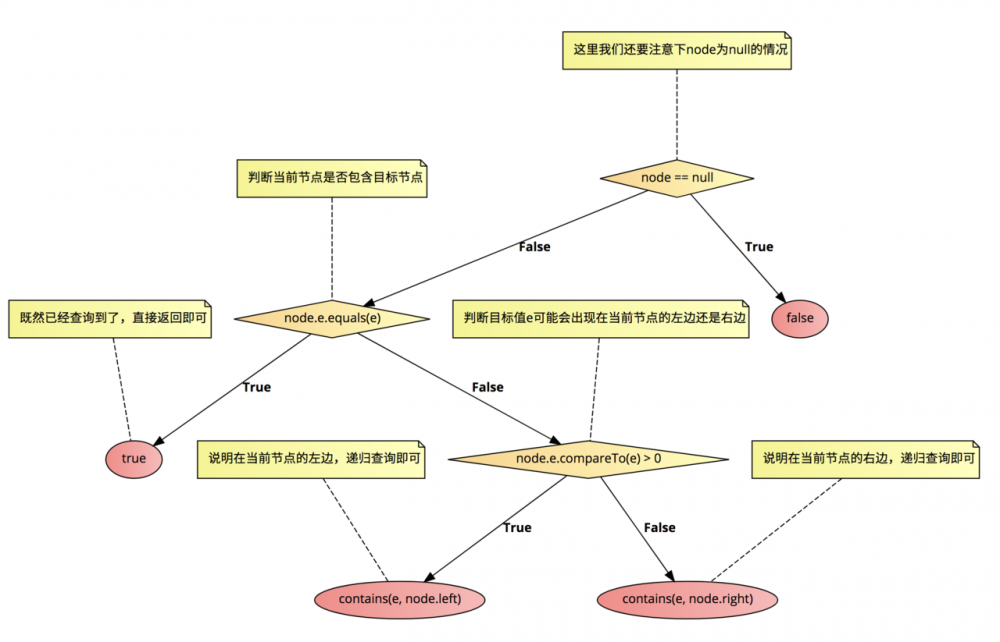 
查询目标值是否存在是非常简单的，但是注意一点，上面的写法我们内部调用的，目的是方便使用递归。我们提供给用户的方法应该是用户只需要传递一个e就行了，然后默认的node参数就是我们的root节点，所以我们可以添加一个这样的共有方法：
public boolean contains(E e){
return contains(e, root);
}
复制代码
插入元素
至于插入元素呢，其实和查询元素的过程非常像。
不过在讨论插入元素之前，我们需要明确一件事，那就是是否允许二分搜索树中存在重复元素。其实允不允许都行，这里我就按照不允许重复元素的情况来处理了。如果在插入过程中，发现了重复元素，那么我们就放弃这次插入。
还是上面的二分搜索树，假设我们希望把31这个元素插入上面的节点。那么前面的过程和查询时的过程一样，我们会来到32这个几点。我们发现31的值比32小，同时32的左子树为null，所以我们就该把31插入到32的左节点就行了。
其实思路和我们之前查找一个元素的思路几乎一模一样，唯一的不同就是这里如果没查找到元素的话，就创建一个新的node节点并把它插入到二叉树中。
伪代码
用伪代码描述的话就是这样的：
if(e的值等于node.e的值){
// 直接返回，什么也不做
return;
}
// 说明我们应该把e插入node的左子树
if(node的值大于e的值){
// 然后我们还要判断下node的左子树是不是null
if(node.left是null){
我们直接以e的值创建一个新的节点;
然后直接插入到这里就行了;
} else{
// 说明node的左子树还有元素，我们需要继续比较，这里使用递归就行了
addToNode(e, node.left);
}
} else {
// 说明我们应该把e插入node的右子树
// 然后我们还要判断下node的右子树是不是null
if(node.right是null){
我们直接以e的值创建一个新的节点;
然后直接插入到这里就行了;
} else{
// 说明node的右子树还有元素，我们需要继续比较，这里使用递归就行了
addToNode(e, node.right);
}
}
复制代码
用图来表示就是这样的: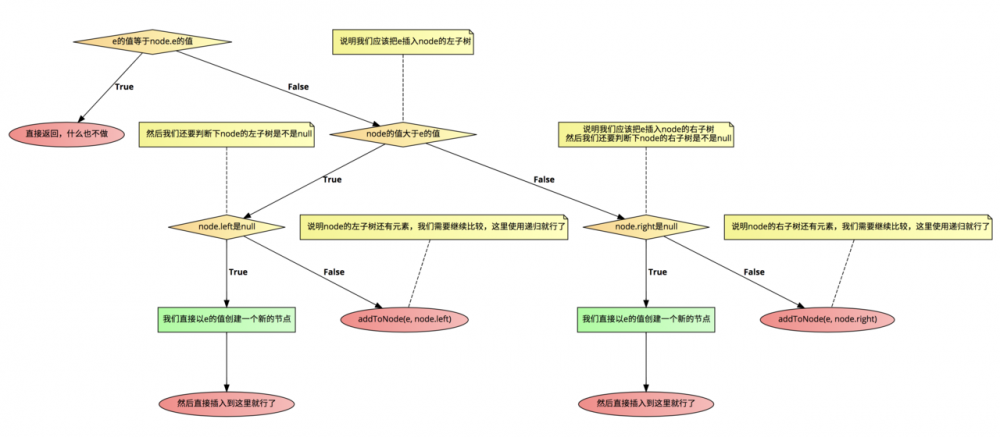 
看起来很复杂，但其实内在逻辑很简单，就是按照上面的规则给我们的新元素安排一个合适的位置，只是在代码中我们要考虑很多可能的因素，所以代码看起来有点的冗余而已。
Java实现
这是代码的基本盘
/**
* @param e 要出入的元素e
* @param node 目标节点
* 将元素e插入到node节点中，
* 如果e和已有的值相等，则忽略这次插入
* 同时手动的确保这个节点node不会为null，这样会方便写代码
*/
private void addToNode(E e, Node node){
}
复制代码
我们就在这个方法中写业务逻辑，然后递归的调用自己。
具体就是这样的
private void addToNode(E e, Node node){
// 相等的话，不做任何事
if (node.e.equals(e)){
return;
}
// 这个值应该被插入左子树
if (node.e.compareTo(e) > 0){
if (node.left == null){
node.left = new Node(e);
size++;
} else {
addToNode(e, node.left);
}
} else {
// 这个值应该被插入右子树
if (node.right == null){
node.right = new Node(e);
size++;
} else {
addToNode(e, node.right);
}
}
}
复制代码
注意下，我们还是需要维护下我们的size变量的。
同样的，我们添加一个公有方法：
public void add(E e){
if (root == null) {
root = new Node(e);
size++;
} else {
addToNode(e, root);
}
}
复制代码
好了，这样我们就完成了向二分搜索树中添加元素了。
测试下查询和删除
其实，无论是查询还是添加，都是很简单的。因为我们在添加过程中，原来的二分搜索树中的各个元素的相对位置是不变的，我们新添加的元素只要寻找到合适的位置就行了。我们新添加元素时不需要移动之前的元素。
然后我们简单的编写代码测试下:
查询元素
@Test
public void contains() {
BSTree<Integer> bsTree = new BSTree<>();
assertFalse(bsTree.contains(3));
bsTree.add(3);
System.out.println(bsTree);
assertTrue(bsTree.contains(3));
}
复制代码
输出结果：
BSTree(root=BSTree.Node(e=3, left=null, right=null), size=1) 复制代码
插入元素
@Test
public void add() {
BSTree<Integer> bsTree = new BSTree<>();
bsTree.add(5);
for (int i = 0; i < 10; i++) {
bsTree.add(i);
System.out.println(bsTree);
}
}
复制代码
输出结果：
BSTree(root=BSTree.Node(e=5, left=BSTree.Node(e=0, left=null, right=null), right=null), size=1) BSTree(root=BSTree.Node(e=5, left=BSTree.Node(e=0, left=null, right=BSTree.Node(e=1, left=null, right=null)), right=null), size=2) BSTree(root=BSTree.Node(e=5, left=BSTree.Node(e=0, left=null, right=BSTree.Node(e=1, left=null, right=BSTree.Node(e=2, left=null, right=null))), right=null), size=3) BSTree(root=BSTree.Node(e=5, left=BSTree.Node(e=0, left=null, right=BSTree.Node(e=1, left=null, right=BSTree.Node(e=2, left=null, right=BSTree.Node(e=3, left=null, right=null)))), right=null), size=4) BSTree(root=BSTree.Node(e=5, left=BSTree.Node(e=0, left=null, right=BSTree.Node(e=1, left=null, right=BSTree.Node(e=2, left=null, right=BSTree.Node(e=3, left=null, right=BSTree.Node(e=4, left=null, right=null))))), right=null), size=5) BSTree(root=BSTree.Node(e=5, left=BSTree.Node(e=0, left=null, right=BSTree.Node(e=1, left=null, right=BSTree.Node(e=2, left=null, right=BSTree.Node(e=3, left=null, right=BSTree.Node(e=4, left=null, right=null))))), right=null), size=5) BSTree(root=BSTree.Node(e=5, left=BSTree.Node(e=0, left=null, right=BSTree.Node(e=1, left=null, right=BSTree.Node(e=2, left=null, right=BSTree.Node(e=3, left=null, right=BSTree.Node(e=4, left=null, right=null))))), right=BSTree.Node(e=6, left=null, right=null)), size=6) BSTree(root=BSTree.Node(e=5, left=BSTree.Node(e=0, left=null, right=BSTree.Node(e=1, left=null, right=BSTree.Node(e=2, left=null, right=BSTree.Node(e=3, left=null, right=BSTree.Node(e=4, left=null, right=null))))), right=BSTree.Node(e=6, left=null, right=BSTree.Node(e=7, left=null, right=null))), size=7) BSTree(root=BSTree.Node(e=5, left=BSTree.Node(e=0, left=null, right=BSTree.Node(e=1, left=null, right=BSTree.Node(e=2, left=null, right=BSTree.Node(e=3, left=null, right=BSTree.Node(e=4, left=null, right=null))))), right=BSTree.Node(e=6, left=null, right=BSTree.Node(e=7, left=null, right=BSTree.Node(e=8, left=null, right=null)))), size=8) BSTree(root=BSTree.Node(e=5, left=BSTree.Node(e=0, left=null, right=BSTree.Node(e=1, left=null, right=BSTree.Node(e=2, left=null, right=BSTree.Node(e=3, left=null, right=BSTree.Node(e=4, left=null, right=null))))), right=BSTree.Node(e=6, left=null, right=BSTree.Node(e=7, left=null, right=BSTree.Node(e=8, left=null, right=BSTree.Node(e=9, left=null, right=null))))), size=9) 复制代码
上述过程的动画演示：
遍历树
对于数组和链表这样的线性数据结构，要是想遍历的话很简单。但是树不一样，遍历的时候需要考虑左右两个子树。
其实遍历操作本身是非常简单的，用一个递归就行了，大致就是：
首先要判断下当前节点是否为null，然后就会发生三种操作
- 访问当前节点
- 递归访问当前节点的左节点
- 递归访问当前节点的右节点
用代码来说就是这样的
function traverse(node){
if (node == null) {
return;
}
process(node);
traverse(node.left);
traverse(node.right);
}
复制代码
但是其实这里有很大的玄机，那就是上面的三种操作的顺序！
上面的三个操作按照排列组合来说有6种情况，你可别小瞧啊，这六种顺序遍历的话，每种遍历方式都有不同的结果。
前序遍历
process(node); traverse(node.left); traverse(node.right); 复制代码
process(node); traverse(node.right); traverse(node.left); 复制代码
这种情况就是先访问当前节点，再递归访问子节点。因为我们是先访问当前节点的，所以这种遍历方式成为前序遍历。然后在前序遍历中，先递归访问左子节点还是先递归访问右子节点一般不重要。
如果的你业务逻辑中，要先处理当前节点的值，再处理子节点的值，就可以使用上面的变量方式。
后序遍历
同理，相信大家也可以猜出后续遍历是什么意思了
traverse(node.left); traverse(node.right); process(node); 复制代码
raverse(node.right); traverse(node.left); process(node); 复制代码
性质和前序遍历刚好相反
中序遍历
traverse(node.left); process(node); traverse(node.right); 复制代码
raverse(node.right); process(node); traverse(node.left); 复制代码
中序遍历的结果的特点是访问的结果是有序的！前者重小到大，后者重大到小！
Java代码
上面几种遍历的代码都是非常简单的，我这里直接贴出来了：
/**
* 中序遍历
* 返回值是按照从小到大的顺序的
* @param node
*/
private void inOrder(Node node){
if (node == null) {
return;
}
inOrder(node.left);
// 在中间
System.out.println(node.e);
inOrder(node.right);
}
public void inOrder(){
inOrder(root);
}
/**
* 前序遍历
* @param node
*/
private void preOrder(Node node){
if (node == null) {
return;
}
// 在前面
System.out.println(node.e);
preOrder(node.left);
preOrder(node.right);
}
public void preOrder(){
preOrder(root);
}
/**
* 后续遍历
* 适用于某些需要先处理子节点的情况
* @param node
*/
private void postOrder(Node node){
if (node == null) {
return;
}
postOrder(node.left);
// 在中间
System.out.println(node.e);
postOrder(node.right);
}
public void postOrder(){
postOrder(root);
}
复制代码
广度优先遍历
// todo
查询、删除最大元素和最小元素
然后我们终于开始编写删除元素的代码了。删除元素的难点在于删除元素可能会扰乱原来的元素之间的相对位置，我们必须提供一些措施来维护我们的二分搜索树，使它继续遵守： 对于每一个节点：它的值大于左子树任意一个节点的值，并且小于其右子树任意一个节点的值 这个规则。
这个问题有点复杂，我们可以先来看看一个简单的情况：查询和删除最大元素和最小元素。
这个问题其实非常简单，我们根据二分搜索树的性质，非常容易的推导出一个结论：二分搜索树的最小值一定出现在树的最左边，也就是不停的 node.left.left... 这样查找；二分搜索树的最大值一定出现在树的最右边，也就是不停的 node.right.right... 这样查找。
思路很简单，我就直接上查询最大最小元素的代码了：
/**
* 寻找这个树中最小的node
* @param node
* @return
*/
private Node findMinimum(Node node){
Node currentNode = node;
while (currentNode.left != null) {
currentNode = currentNode.left;
}
return currentNode;
}
public E findMinimum(){
if (root == null) {
throw new RuntimeException(":evergreen_tree:中没有元素了");
}
return findMinimum(root).e;
}
/**
* 寻找这个树中最大的node
* 就是类似链表操作，一直向最右边查找
* @param node
* @return
*/
private Node findMaximum(Node node){
Node currentNode = node;
while (currentNode.right != null) {
currentNode = currentNode.right;
}
return currentNode;
}
public E findMaximum(){
if (root == null) {
throw new RuntimeException(":evergreen_tree:中没有元素了");
}
return findMaximum(root).e;
}
复制代码
一个while循环就行了，当然你要是想用递归的算法也行。其实上面的代码等价于寻找链表的最后一个元素。
然后我们来思考下删除元素应该怎么做。
我们的最小元素或最大元素有两种情况：是叶子节点或者不是叶子节点。
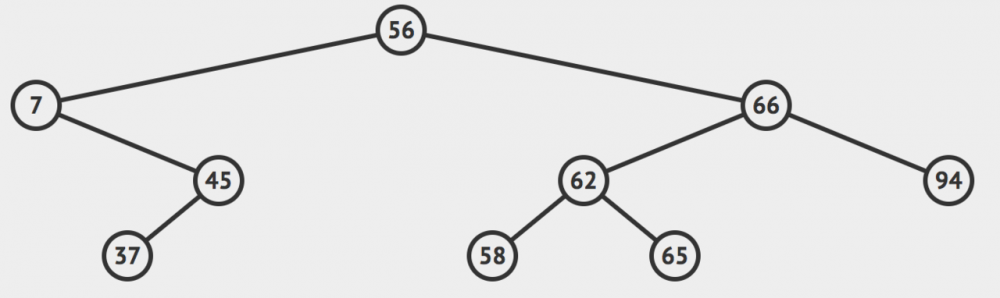
上面这个图中，元素94就是一个叶子节点，我们删除的时候非常简单，删除掉它就行了。
但是我们的最小节点7不一样，它不是叶子节点，我们把它删除了之后，还需要把原来的7的右节点重新拼凑到原来的树上。参考这样的动画：
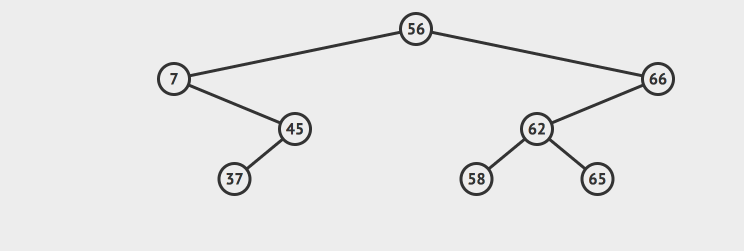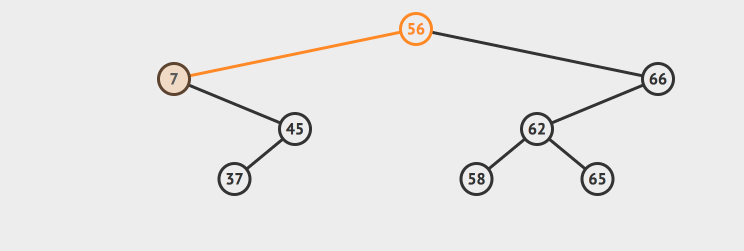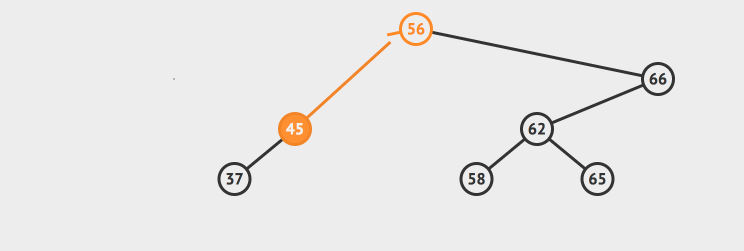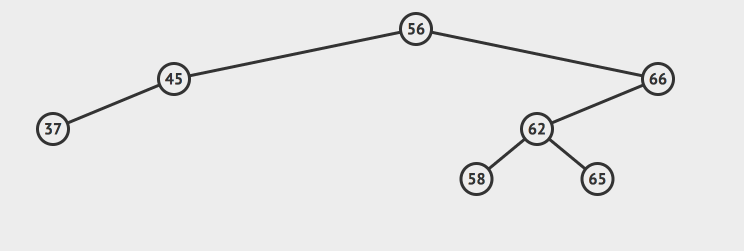
不过这里重新拼接的逻辑很简单，因为我们根据二分搜索树的性质，可以推导出：节点7的右节点的所有的元素的值一定小于7的父节点，所以我们只需要非常简单的把7的右子树拼接到7的父节点上就行了，不需要一些额外的工作了。
其实你只要想明白这一点就行了。
我们在删除元素之前需要判断一下：
- 如果当前节点是叶子节点，直接删除；
- 否者需要把当前的节点的左子树或者右子树拼接到其父节点的位置。
我们以删除最小元素为例。这是代码的基本骨架
/**
* 删除给定node的最小节点
* 并返回 <strong>删除节点后新的二分搜索树的的根</strong>
* 这个定义很重要，可以让我们的编码更加的方便
* @param node
* @return
*/
private Node removeMin(Node node){
}
复制代码
这个方法的目的很明确，就是传进来一个二分搜索树的根节点，我们要删除它的最小元素。
其实呢，我们定义方法时主要要考虑如何让我们的编码变得简单。我上面的定义中，就是如果传进来的是7这个节点，那么我们期望的返回值就是：以7为根节点的二分搜索树删除最小元素后的新的二分搜索树。
额，我也觉得很绕口，我们看图说话：
假如传进来是这样的树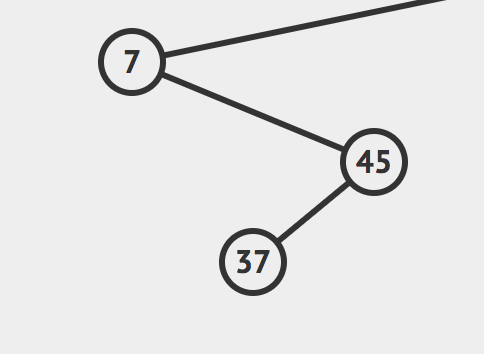 
那么期望的返回值就是这样的树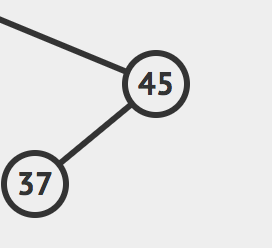 
同样的：
如果传进来的是这样的树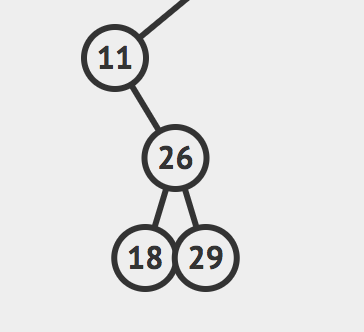 
那么返回值就是这样的树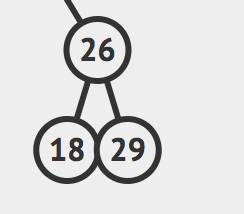 
这下清楚了吧。
这样设计方法主要是方便我们写递归代码，至于为什么想到这种方式，那就是只可意会，不可言传了。
这是代码的基本框架，这样写还是为了递归以及后面的复用。
private Node removeMin(Node node){
}
复制代码
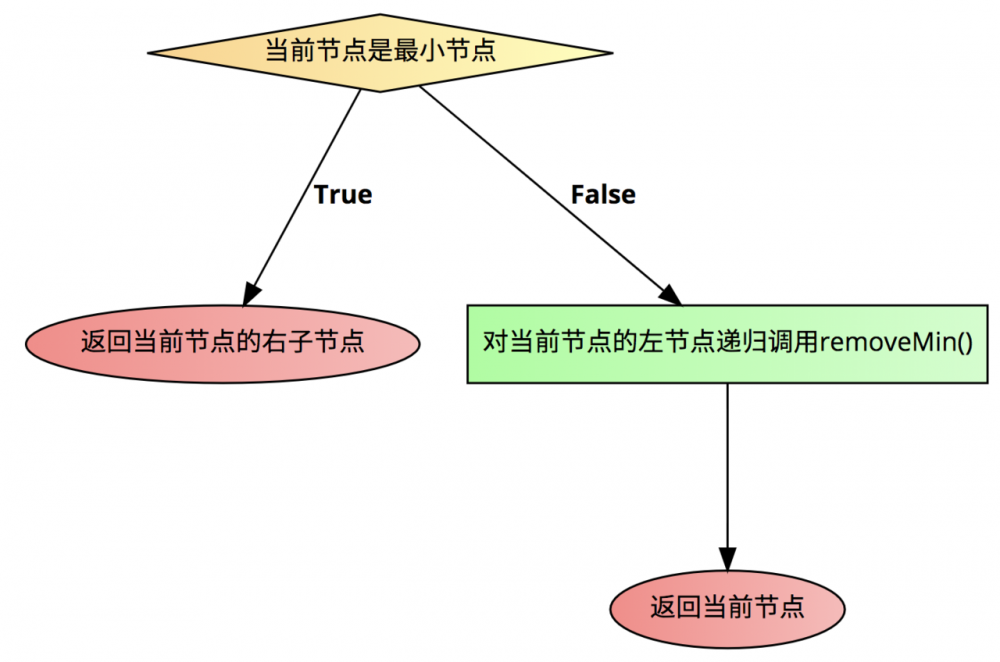
我们的方法的具体的逻辑可以这样写
if(当前节点是最小节点){
return 当前节点的右子节点;
} else{
对当前节点的左节点递归调用removeMin();
return 当前节点;
}
复制代码
可以看到，代码逻辑是非常简单的，就是一开始的时候有地点技巧性。
Java代码
private Node removeMin(Node node){
// 当前节点就是最小节点
if (node.left == null) {
Node rightNode = node.right;
node.right = null;
size--;
return rightNode;
} else {
node.left = removeMin(node.left);
return node;
}
}
public E removeMin(){
if (root == null) {
throw new RuntimeException("你的树已经没有元素了");
}
E e = findMinimum();
root = removeMin(root);
return e;
}
复制代码
然后删除最大元素的逻辑和之前的删除最小元素一模一样，只是把left这个单词替换成right这个单词就行了，我直接上代码了：
/**
* 删除给定node的最大节点
* 并返回 <strong>删除节点后新的二分搜索树的的根</strong>
* 这个定义很重要，可以让我们的编码更加的方便
* @param node
* @return
*/
private Node removeMax(Node node){
// 当前节点就是最小节点
if (node.right == null) {
Node rightNode = node.left;
node.left = null;
size--;
return rightNode;
} else {
node.right = removeMax(node.right);
return node;
}
}
/**
* 这里我们把寻找最小值和删除最小值给分开
* 简化的编码的逻辑
* @return
*/
public E removeMax(){
if (root == null) {
throw new RuntimeException("你的树已经没有元素了");
}
E e = findMaximum();
root = removeMax(root);
return e;
}
复制代码
删除任意一个元素
关于删除任意一个元素的问题，之前卖了很多关子。其实它的代码真正实现的时候非常的简单，就是有点技巧性，很难想到这种解法。
假设我们要删除一个元素，那么这个元素可能有三种情况：
- 当前元素没有子节点
- 当前元素有一个字节点
- 当前元素有两个子节点
如果当前元素没有子节点，那就太简单了，直接删除它就行了。
如果当前元素有一个字节点，也很简单。因为我们可以直接删除当前节点，然后把当前节点的子节点直接给顶上去。这样是不会破坏二分搜索树性质，这一点我们在之前讲删除最小元素的时候已经说过了。
现在问题就在于如果当前元素有两个只节点怎么办？
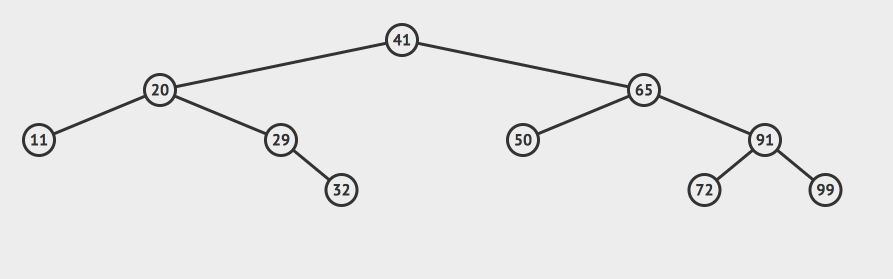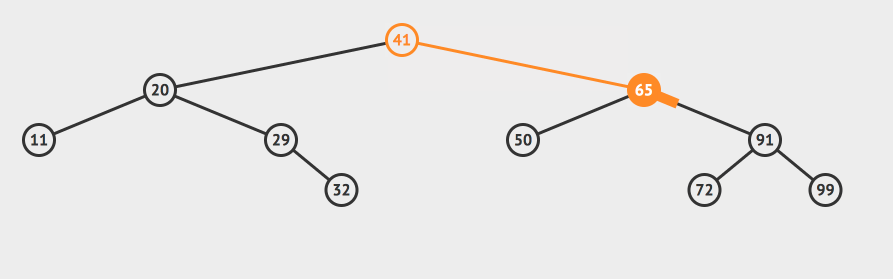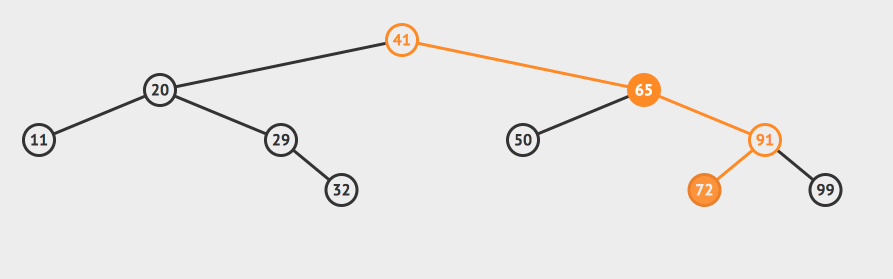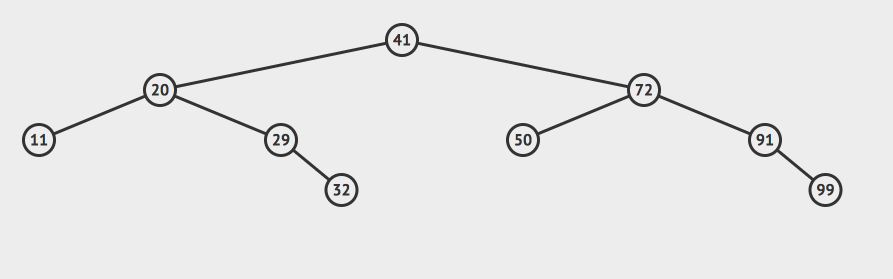
比如这里，我们想删除值为65的节点怎么办？
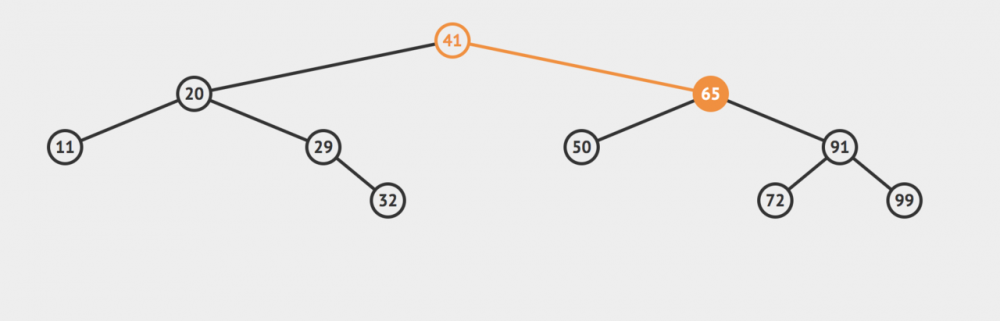
这个节点有两个子节点。如果直接删除的话，我们的二叉树会被分成三块：根二叉树、65的左子树以及65的右子树。
我们不能说简单的把65给删除之后就不管了，我们还要把它们拼接在一起才行啊。
但是我们怎么拼接呢？
直接把65的左子树或者右子树顶上去？不行，这样做显然不符合二叉树的性质。
其实呢你可以换一种思路：我们刚才是因为把65这个节点删除了，然后导致我们的二叉树分裂了。现在我们只要寻找到一个新的节点来代替65原来的位置就行了！找一个备胎顶上！
但是问题是，这个备胎到哪里找呢？我们为了维护二分搜索树的性质，我们的备胎必须具有下面的性质
-
比65所有的左节点小，
-
比65所有的右节点大
-
比65的父节点大
备注：因为65是它父节点的右子节点，所以这个备胎应该比65的父节点大；如果要删除的节点是它父节点的左子节点，那么这备胎应该比要删除的节点的父节点小。
好了，这里大家明白了不？
如果你还是不清楚，请仔细的观察上面的二叉树，看看哪个节点满足这个要求？
。。。 。。。
答案就是72或者50，用这个两个节点中的任意一个代替65都行。
但是本质是什么？ 50是65左子树的最大值，72是65右子树的最小值！！
一个结论： 假如我们要删除一个节点A，那么我们只要把A右子树中最小的节点B找出来，用B顶替A节点就行了 。
其实这个结论很容易证明：根据二分搜索树的性质：B节点一定大于A的左子树的所有节点，一定小于A的右子树的其他节点。而其他的节点的相对位置没有变化。用B代替A后，我们的二叉树显然还是一个二分搜索树。
这个删除过程用动画演示就是这样的：
编码思路
那么我们怎么用代码来写呢？其实只要这几步
- 寻找到要删除的节点
这是一个查询节点的过程，我们之前已经说了
- 对当前节点进行分类讨论
- 如果它没有子节点，直接删除
- 如果它有一个子节点，按照我们之前删除最大元素的逻辑来处理
- 如果它有两个子节点，那么就用它右子树的最小节点来代替它
Java代码
private Node remove(E e, Node node){
if (node == null){
return null;
}
if (e.compareTo(node.e) < 0) {
node.left = remove(e, node.left);
return node;
} else if (e.compareTo(node.e) > 0) {
node.right = remove(e, node.right);
return node;
} else { // e == node.e
if (node.left == null) {
Node rightNode = node.right;
node.right = null;
size--;
return rightNode;
} else if (node.right == null) {
Node leftNode = node.left;
node.left = null;
size--;
return leftNode;
} else { // 左右子树都不为空
// 找到比要删除节点大的最小节点（或者小的最大节点）
// 用这个节点代替他
Node successor = removeMin(node.right);
node.e = successor.e;
return node;
}
}
}
public void remove(E e){
root = remove(e, root);
}
复制代码
小结
下面就是这个二叉搜索树的全部代码
import lombok.Getter;
import lombok.ToString;
import java.util.LinkedList;
import java.util.Queue;
/**
* 二分搜索树
* @param <E>
*/
@ToString
public class BSTree<E extends Comparable<E>> {
private Node root;
@Getter
private int size;
public BSTree() {
}
public boolean isEmpty(){
return size == 0;
}
/**
* @param e 要出入的元素e
* @param node 目标节点
* 将元素e插入到node节点中，
* 如果e和已有的值相等，则忽略这次插入
* 同时手动的确保这个节点node不会为null，这样会方便写代码
*
* O(h)的复杂度 h为:evergreen_tree:的高度，一般为log(n)
*/
private void addToNode(E e, Node node){
// 相等的话，不做任何事
if (node.e.equals(e)){
return;
}
// 这个值应该被插入左子树
if (node.e.compareTo(e) > 0){
if (node.left == null){
node.left = new Node(e);
size++;
} else {
addToNode(e, node.left);
}
} else {
// 这个值应该被插入右子树
if (node.right == null){
node.right = new Node(e);
size++;
} else {
addToNode(e, node.right);
}
}
}
public void add(E e){
if (root == null) {
root = new Node(e);
size++;
} else {
addToNode(e, root);
}
}
/**
* 看看这个节点以及它的子节点是不是包含e
* @param e 要查找的元素
* @param node 目标节点
* @return 当前二叉搜索树是否包含目标值
*/
private boolean contains(E e, Node node){
// 这里我们还要注意下node为null的情况
if (node == null) {
return false;
}
// 判断当前节点是否包含目标节点
if (node.e.equals(e)){
// 既然已经查询到了，直接返回即可
return true;
// 判断目标值e可能会出现在当前节点的左边还是右边
} else if (node.e.compareTo(e) > 0) {
// 说明在当前节点的左边，递归查询即可
return contains(e, node.left);
} else {
// 说明在当前节点的右边，递归查询即可
return contains(e, node.right);
}
}
public boolean contains(E e){
return contains(e, root);
}
/**
* 中序遍历
* 返回值是按照从小到大的顺序的
* @param node
*/
private void inOrder(Node node){
if (node == null) {
return;
}
inOrder(node.left);
// 在中间
System.out.println(node.e);
inOrder(node.right);
}
public void inOrder(){
inOrder(root);
}
/**
* 前序遍历
* @param node
*/
private void preOrder(Node node){
if (node == null) {
return;
}
// 在前面
System.out.println(node.e);
preOrder(node.left);
preOrder(node.right);
}
public void preOrder(){
preOrder(root);
}
/**
* 后续遍历
* 适用于某些需要先处理子节点的情况
* @param node
*/
private void postOrder(Node node){
if (node == null) {
return;
}
postOrder(node.left);
// 在中间
System.out.println(node.e);
postOrder(node.right);
}
public void postOrder(){
postOrder(root);
}
/**
* 按照层级广度优先遍历
* 通过一个队列来存储下一个层级的节点
* 每次遍历当前的节点后将当前节点的左右子树添加到队列中
*/
public void levelOrder(){
Queue<Node> queue = new LinkedList<>();
if (root == null) {
return;
}
queue.add(root);
while (!queue.isEmpty()){
Node currentNode = queue.remove();
System.out.println(currentNode.e);
if (currentNode.left != null){
queue.add(currentNode.left);
}
if (currentNode.right != null){
queue.add(currentNode.right);
}
}
}
/**
* 寻找这个树中最小的node
* @param node
* @return
*/
private Node findMinimum(Node node){
Node currentNode = node;
while (currentNode.left != null) {
currentNode = currentNode.left;
}
return currentNode;
}
public E findMinimum(){
if (root == null) {
throw new RuntimeException(":evergreen_tree:中没有元素了");
}
return findMinimum(root).e;
}
/**
* 寻找这个树中最大的node
* 就是类似链表操作，一直向最右边查找
* @param node
* @return
*/
private Node findMaximum(Node node){
Node currentNode = node;
while (currentNode.right != null) {
currentNode = currentNode.right;
}
return currentNode;
}
public E findMaximum(){
if (root == null) {
throw new RuntimeException(":evergreen_tree:中没有元素了");
}
return findMaximum(root).e;
}
/**
* 删除给定node的最小节点
* 并返回 <strong>删除节点后新的二分搜索树的的根</strong>
* 这个定义很重要，可以让我们的编码更加的方便
* @param node
* @return
*/
private Node removeMin(Node node){
// 当前节点就是最小节点
if (node.left == null) {
Node rightNode = node.right;
node.right = null;
size--;
return rightNode;
} else {
node.left = removeMin(node.left);
return node;
}
}
/**
* 这里我们把寻找最小值和删除最小值给分开
* 简化的编码的逻辑
* @return
*/
public E removeMin(){
if (root == null) {
throw new RuntimeException("你的树已经没有元素了");
}
E e = findMinimum();
root = removeMin(root);
return e;
}
/**
* 删除给定node的最大节点
* 并返回 <strong>删除节点后新的二分搜索树的的根</strong>
* 这个定义很重要，可以让我们的编码更加的方便
* @param node
* @return
*/
private Node removeMax(Node node){
// 当前节点就是最小节点
if (node.right == null) {
Node rightNode = node.left;
node.left = null;
size--;
return rightNode;
} else {
node.right = removeMax(node.right);
return node;
}
}
/**
* 这里我们把寻找最小值和删除最小值给分开
* 简化的编码的逻辑
* @return
*/
public E removeMax(){
if (root == null) {
throw new RuntimeException("你的树已经没有元素了");
}
E e = findMaximum();
root = removeMax(root);
return e;
}
private Node remove(E e, Node node){
if (node == null){
return null;
}
if (e.compareTo(node.e) < 0) {
node.left = remove(e, node.left);
return node;
} else if (e.compareTo(node.e) > 0) {
node.right = remove(e, node.right);
return node;
} else { // e == node.e
if (node.left == null) {
Node rightNode = node.right;
node.right = null;
size--;
return rightNode;
} else if (node.right == null) {
Node leftNode = node.left;
node.left = null;
size--;
return leftNode;
} else { // 左右子树都不为空
// 找到比要删除节点大的最小节点（或者小的最大节点）
// 用这个节点代替他
Node successor = removeMin(node.right);
node.e = successor.e;
return node;
}
}
}
public void remove(E e){
root = remove(e, root);
}
@ToString
private class Node{
public E e;
public Node left, right;
public Node(E e){
this.e = e;
}
}
}
复制代码
同步于GitHub github.com/fish-stack/…
正文到此结束
热门推荐
相关文章
近期评论
-
文章和留言都翻到11页了 没有OOM
-
-
朋友，翻页到11页，及以后，会出现OOM，无法访问
-
-
搞个gitee的项目
-
-
版本号是多少，你可以下载哪个代码仓库，jdk选1.8 直接跑就行
-
-
-
Loading...
![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)
