Java八大排序算法之归并排序
一、动图演示
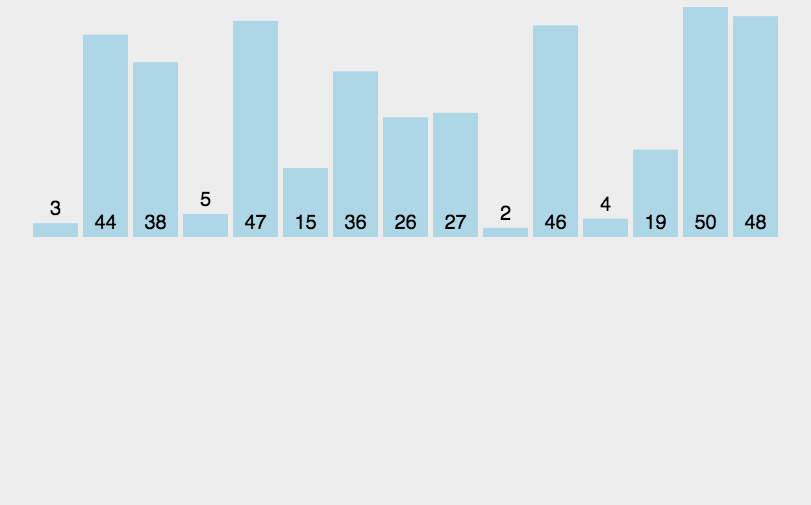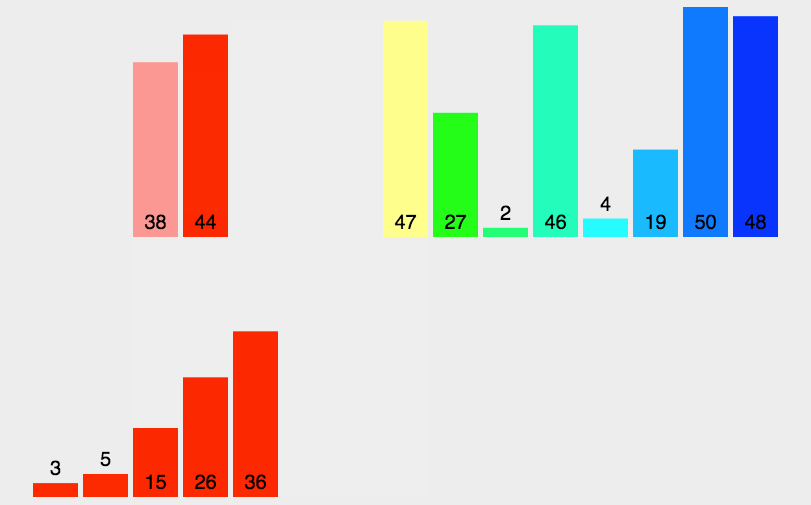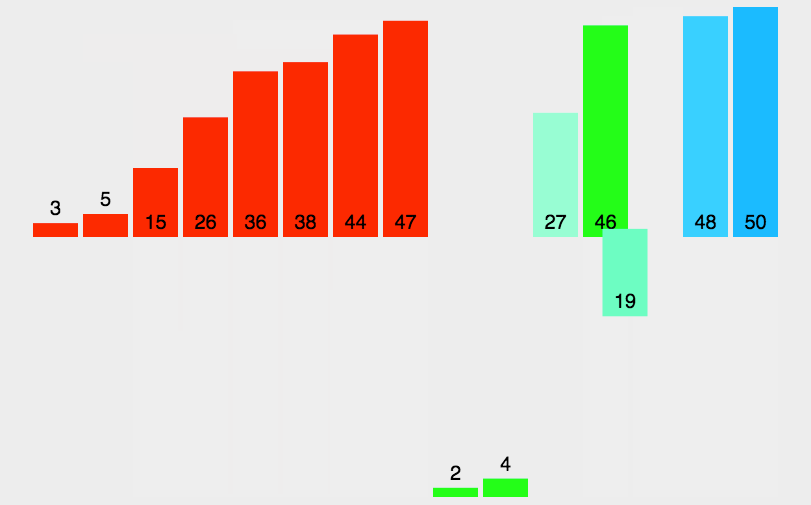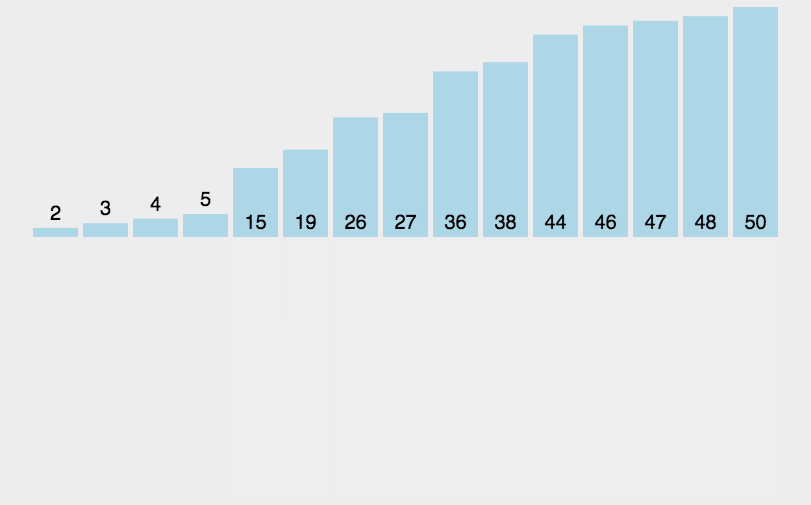
二、思路分析
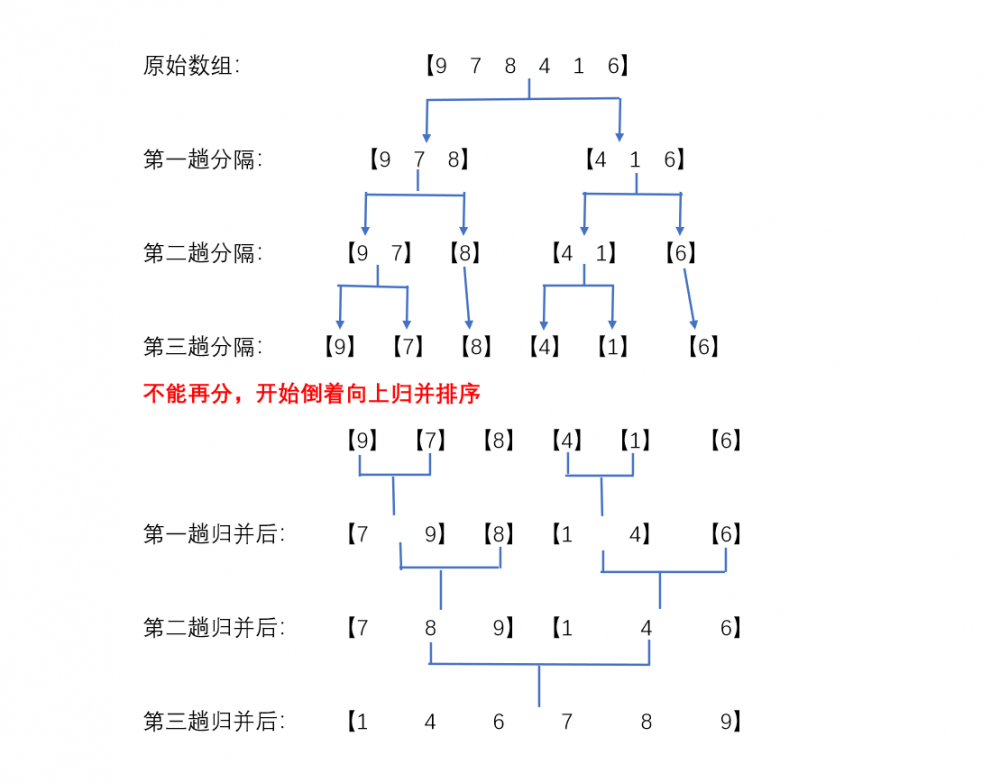
归并排序就是递归得将原始数组递归对半分隔，直到不能再分（只剩下一个元素）后，开始从最小的数组向上归并排序
1. 向上归并排序的时候，需要一个暂存数组用来排序，
2. 将待合并的两个数组，从第一位开始比较，小的放到暂存数组，指针向后移，
3. 直到一个数组空，这时，不用判断哪个数组空了，直接将两个数组剩下的元素追加到暂存数组里，
4. 再将暂存数组排序后的元素放到原数组里，两个数组合成一个，这一趟结束。
根据思路分析，每一趟的执行流程如下图所示：
三、负杂度分析
1. 时间复杂度：递归算法的时间复杂度公式：T[n] = aT[n/b] + f(n)
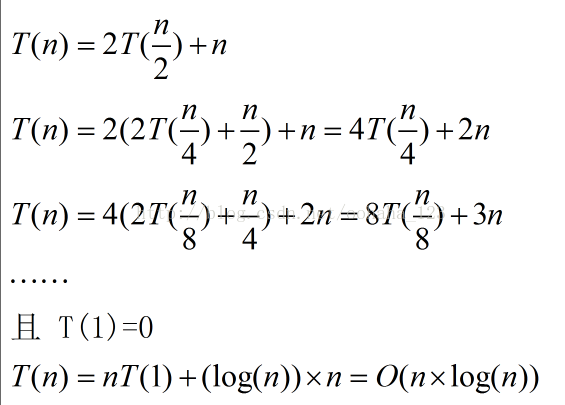
无论原始数组是否是有序的，都要递归分隔并向上归并排序，所以时间复杂度始终是O（nlog2n）
2. 空间复杂度：
每次两个数组进行归并排序的时候，都会利用一个长度为n的数组作为辅助数组用于保存合并序列，所以空间复杂度为O（n）
四、Java 代码如下
import java.util.Arrays;
public class Main {
public static void main(String[] args) {
int[] arr = new int[]{3,6,4,7,5,2};
merge(arr,0,arr.length-1);
System.out.println(Arrays.toString(arr));
}
//归并
public static void merge(int[] arr,int low,int high){
int center = (high+low)/2;
if(low<high){
//递归，直到low==high，也就是数组已不能再分了，
merge(arr,low,center);
merge(arr,center+1,high);
//当数组不能再分，开始归并排序
mergeSort(arr,low,center,high);
System.out.println(Arrays.toString(arr));
}
}
//排序
public static void mergeSort(int[] arr,int low,int center,int high){
//用于暂存排序后的数组的临时数组
int[] tempArr = new int[arr.length];
int i = low,j = center+1;
//临时数组的下标
int index = 0;
//循环遍历两个数组的数字，将小的插入到临时数组里
while(i<=center && j<= high){
//左边数组的数小，插入到新数组
if(arr[i]<arr[j]){
tempArr[index] = arr[i];
i++;
}else{//右边数组的数小，插入到新数组
tempArr[index] = arr[j];
j++;
}
index++;
}
//处理左半边数组多余的数据，将左半边多余的数据直接追加的临时数组的后面
while(i<=center){
tempArr[index] = arr[i];
i++;
index++;
}
//处理右半边数组多余的数据，将右半边多余的数据直接追加的临时数组的后面
while(j<= high){
tempArr[index] = arr[j];
j++;
index++;
}
//将临时数组中的数据重新放进原数组
for (int k = 0; k < index; k++) {
arr[k+low] = tempArr[k];
}
}
}
Linux公社的RSS地址 ： https://www.linuxidc.com/rssFeed.aspx
本文永久更新链接地址： https://www.linuxidc.com/Linux/2019-08/159804.htm
正文到此结束
热门推荐
相关文章
近期评论
-
666
-
文章和留言都翻到11页了 没有OOM
-
-
朋友，翻页到11页，及以后，会出现OOM，无法访问
-
-
-
-
版本号是多少，你可以下载哪个代码仓库，jdk选1.8 直接跑就行
-
-
Loading...
![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)
