JDK源码分析-PriorityQueue

概述

PriorityQueue 意为优先队列，表示队列中的元素是有优先级的，也就是说元素之间是可比较的。因此，插入队列的元素要实现 Comparable 接口或者 Comparator 接口。

PriorityQ ueue  的继承结构如下：

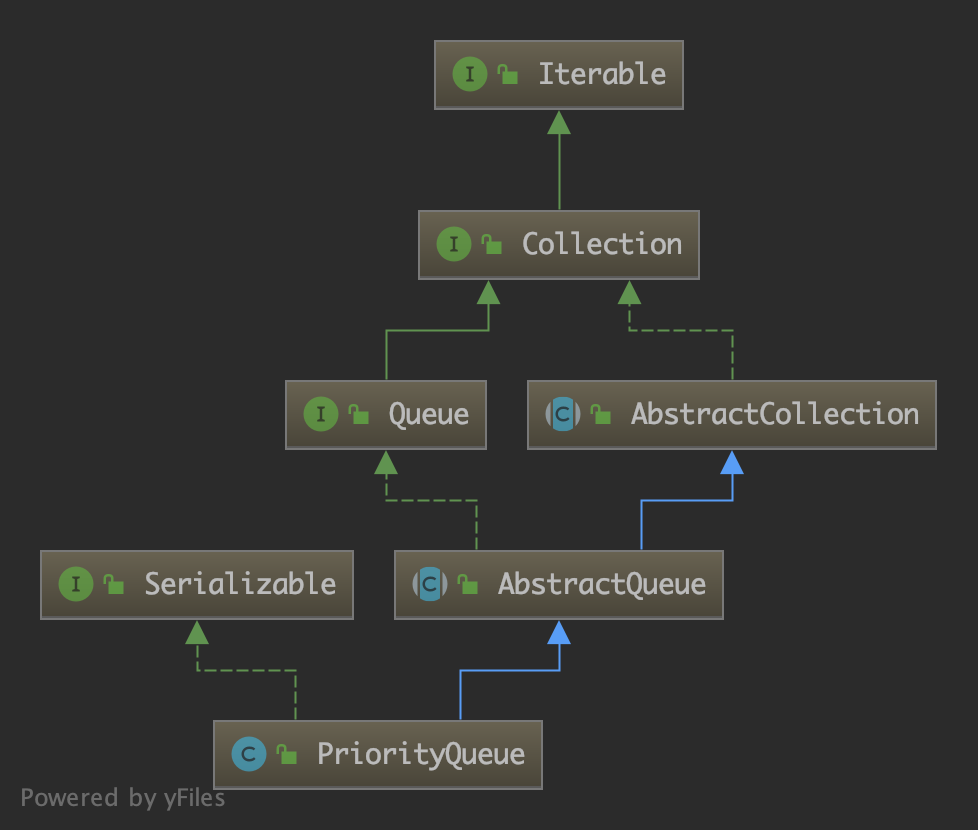
PriorityQueue 没有实现 BlockingQueue 接口，并非阻塞队列。 它在逻辑上使用「堆」（即完全二叉树）结构实现，物理上基于「动态数组」存储。如图所示：

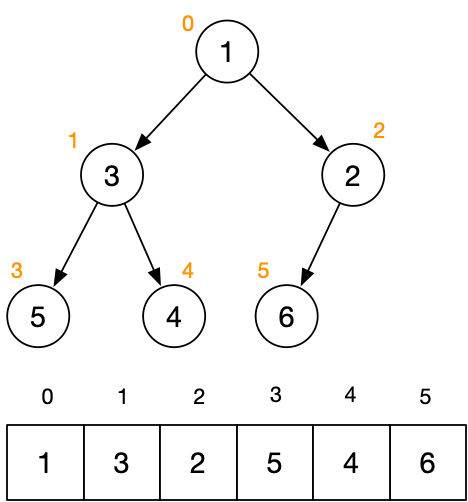
有关堆的概念可参考前文「 数据结构与算法笔记（三） 」的相关描述。下面分析其代码实现。

代码分析

成员变量

// 数组的默认初始容量

private static final int DEFAULT_INITIAL_CAPACITY = 11;

// 内部数组，用于存储队列中的元素

transient Object[] queue; // non-private to simplify nested class access

// 队列中元素的个数

private int size = 0;

// 队列中元素的比较器

private final Comparator<? super E> comparator;

// 结构性修改次数

transient int modCount = 0; // non-private to simplify nested class access

构造器

// 构造器 1：无参构造器（默认初试容量为 11）

public PriorityQueue() {

this(DEFAULT_INITIAL_CAPACITY, null);

}

// 构造器 2：指定容量的构造器

public PriorityQueue(int initialCapacity) {

this(initialCapacity, null);

}

// 构造器 3：指定比较器的构造器

public PriorityQueue(Comparator<? super E> comparator) {

this(DEFAULT_INITIAL_CAPACITY, comparator);

}

// 构造器 4：指定初始容量和比较器的构造器

public PriorityQueue(int initialCapacity,

Comparator<? super E> comparator) {

// Note: This restriction of at least one is not actually needed,

// but continues for 1.5 compatibility

if (initialCapacity < 1)

throw new IllegalArgumentException();

// 初始化内部数组和比较器

this.queue = new Object[initialCapacity];

this.comparator = comparator;

}

这几个构造器的作用就是初始化内部数组和比较器。

此外，还有几个稍复杂点的构造器，代码如下：

// 构造器 5：用给定集合初始化 PriorityQueue 对象

public PriorityQueue(Collection<? extends E> c) {

// 如果集合是 SortedSet 类型

if (c instanceof SortedSet<?>) {

SortedSet<? extends E> ss = (SortedSet<? extends E>) c;

this.comparator = (Comparator<? super E>) ss.comparator();

initElementsFromCollection(ss);

}

// 如果集合是 PriorityQueue 类型

else if (c instanceof PriorityQueue<?>) {

PriorityQueue<? extends E> pq = (PriorityQueue<? extends E>) c;

this.comparator = (Comparator<? super E>) pq.comparator();

initFromPriorityQueue(pq);

}

else {

this.comparator = null;

initFromCollection(c);

}

}

initElementsFromCollection:

// 使用给定集合的元素初始化 PriorityQueue

private void initElementsFromCollection(Collection<? extends E> c) {

// 把集合转为数组

Object[] a = c.toArray();

// If c.toArray incorrectly doesn't return Object[], copy it.

if (a.getClass() != Object[].class)

a = Arrays.copyOf(a, a.length, Object[].class);

int len = a.length;

// 确保集合中每个元素不能为空

if (len == 1 || this.comparator != null)

for (int i = 0; i < len; i++)

if (a[i] == null)

throw new NullPointerException();

// 初始化 queue 数组和 size

this.queue = a;

this.size = a.length;

}

initFromPriorityQueue:

private void initFromPriorityQueue(PriorityQueue<? extends E> c) {

if (c.getClass() == PriorityQueue.class) {

// 若给定的是 PriorityQueue，则直接进行初始化

this.queue = c.toArray();

this.size = c.size();

} else {

initFromCollection(c);

}

}

initFromCollection:

private void initFromCollection(Collection<? extends E> c) {

// 将集合中的元素转为数组，并赋值给 queue（上面已分析）

initElementsFromCollection(c);

// 堆化

heapify();

}

heapify: 堆化，即将数组元素转为堆的存储结构

private void heapify() {

// 从数组的中间位置开始遍历即可

for (int i = (size >>> 1) - 1; i >= 0; i--)

siftDown(i, (E) queue[i]);

}

PS: 这里遍历时，从数组的中间位置遍历（根据堆的存储结构，如果某个节点的索引为 i，则其左右子节点的索引分别为 2 * i + 1,   2 * i + 2）。

siftDown: 向下筛选？暂未找到恰当的译法，但这不是重点，该方法的作用就是使数组满足堆结构（其思想与冒泡排序有些类似）。如下：

private void siftDown(int k, E x) {

// 根据 comparator 是否为空采用不同的方法

if (comparator != null)

siftDownUsingComparator(k, x);

else

siftDownComparable(k, x);

}

siftDownUsingComparator:

private void siftDownUsingComparator(int k, E x) {

// 数组的中间位置

int half = size >>> 1;

while (k < half) {

// 获取索引为 k 的节点的左子节点索引

int child = (k << 1) + 1;

// 获取 child 的值

Object c = queue[child];

// 获取索引为 k 的节点的右子节点索引

int right = child + 1;

// 左子节点的值大于右子节点，则二者换位置

if (right < size &&

comparator.compare((E) c, (E) queue[right]) > 0)

// 取左右子节点中较小的一个

c = queue[child = right];

// 给定的元素 x 与较小的子节点的值比较

if (comparator.compare(x, (E) c) <= 0)

break;

// 将该节点与子节点互换

queue[k] = c;

k = child;

}

queue[k] = x;

}

该方法的步骤大概：

1. 找出给定节点（父节点）的子节点中较小的一个，并于之比较大小；

2. 若父节点较大，则交换位置（父节点“下沉”）。

PS: 可参考上面的结构示意图， 其中数组表示队列中现有的元素，二叉树表示相应的堆结构， 角标表示数组中的索引（有兴趣可以在 IDE 断点调试验证）。

siftDownComparable 方法代码如下：

private void siftDownComparable(int k, E x) {

Comparable<? super E> key = (Comparable<? super E>)x;

int half = size >>> 1; // loop while a non-leaf

while (k < half) {

int child = (k << 1) + 1; // assume left child is least

Object c = queue[child];

int right = child + 1;

if (right < size &&

((Comparable<? super E>) c).compareTo((E) queue[right]) > 0)

c = queue[child = right];

if (key.compareTo((E) c) <= 0)

break;

queue[k] = c;

k = child;

}

queue[k] = key;

}

此方法与 siftDownUsingComparator 方法实现逻辑完全一样，不同的的地方仅在于该方法是针对 Comparable 接口，而后者针对 Comparator 接口，不再赘述。

此外 PriorityQueue 还有两个构造器，但都是通过上面的方法实现的，如下：

// 构造器 6：用给定的 PriorityQueue 初始化一个 PriorityQueue

public PriorityQueue(PriorityQueue<? extends E> c) {

this.comparator = (Comparator<? super E>) c.comparator();

initFromPriorityQueue(c);

}

// 构造器 7：用给定的 SortedSet 初始化 PriorityQueue

public PriorityQueue(SortedSet<? extends E> c) {

this.comparator = (Comparator<? super E>) c.comparator();

initElementsFromCollection(c);

}

也不再赘述。

入队操作 ：add(E), offer(E)

两个入队操作方法如下：

// 实际是调用 offer 方法实现的

public boolean add(E e) {

return offer(e);

}

public boolean offer(E e) {

if (e == null)

throw new NullPointerException();

modCount++;

int i = size;

// 扩容

if (i >= queue.length)

grow(i + 1);

// 元素个数加一

size = i + 1;

// 原数组为空，即添加第一个元素，直接放到数组首位即可

if (i == 0)

queue[0] = e;

else

// 向上筛选？

siftUp(i, e);

return true;

}

扩容操作：

private static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8;

private void grow(int minCapacity) {

// 原先容量

int oldCapacity = queue.length;

// Double size if small; else grow by 50%

// 原容量较小时，扩大为原先的两倍；否则扩大为原先的 1.5 倍

int newCapacity = oldCapacity + ((oldCapacity < 64) ?

(oldCapacity + 2) :

(oldCapacity >> 1));

// overflow-conscious code

if (newCapacity - MAX_ARRAY_SIZE > 0)

newCapacity = hugeCapacity(minCapacity);

// 创建一个新的数组

queue = Arrays.copyOf(queue, newCapacity);

}

private static int hugeCapacity(int minCapacity) {

if (minCapacity < 0) // overflow

throw new OutOfMemoryError();

return (minCapacity > MAX_ARRAY_SIZE) ?

Integer.MAX_VALUE :

MAX_ARRAY_SIZE;

}

PS: 扩容操作与前文分析的 ArrayList 和 Vector 的扩容操作类似。

siftUp: 可与 siftDown 方法对比分析

private void siftUp(int k, E x) {

if (comparator != null)

siftUpUsingComparator(k, x);

else

siftUpComparable(k, x);

}

siftUpUsingComparator():

private void siftUpUsingComparator(int k, E x) {

while (k > 0) {

// 父节点的索引

int parent = (k - 1) >>> 1;

// 父节点的元素

Object e = queue[parent];

// 若该节点元素大于等于父节点，结束循环

if (comparator.compare(x, (E) e) >= 0)

break;

// 该节点元素小于父节点，

queue[k] = e;

k = parent;

}

// 入队

queue[k] = x;

}

该操作也稍微有点绕，还是以上图为基础继续操作，示意图如下：

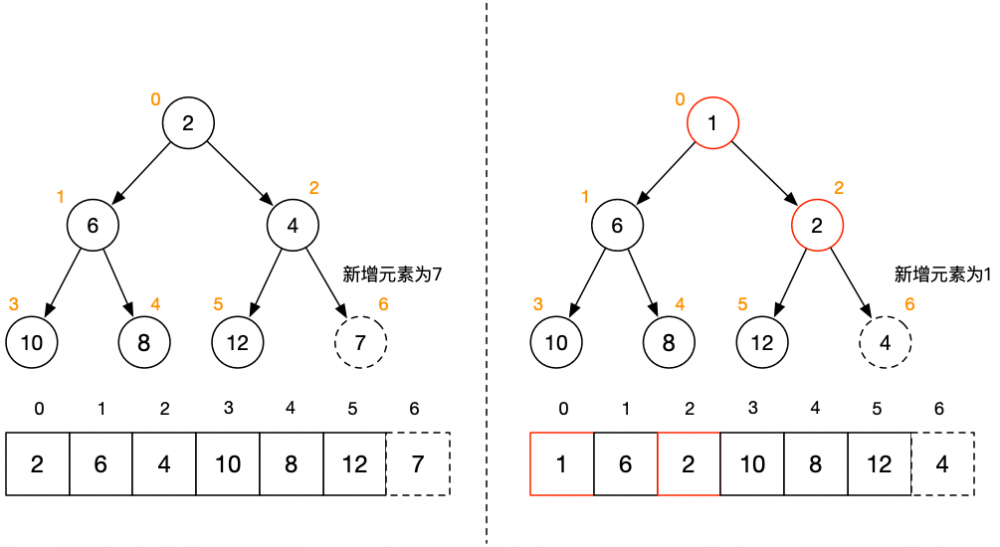
其中分为左右两种情况：

1. 左边插入元素为 7，大于父节点 4，无需和父节点交换位置，直接插入即可；

2. 右边插入元素为 1，小于父节点 4，需要和父节点交换位置，并一直往上查找和交换，上图为调整后的数组及对应的树结构。

siftUpComparable: 

private void siftUpComparable(int k, E x) {

Comparable<? super E> key = (Comparable<? super E>) x;

while (k > 0) {

int parent = (k - 1) >>> 1;

Object e = queue[parent];

if (key.compareTo((E) e) >= 0)

break;

queue[k] = e;

k = parent;

}

queue[k] = key;

}

该方法逻辑与 siftUpUsingComparator 一样，也是 Comparator 和 Comparable 接口的差别。

这里简单比较下  siftDown 和  siftUp 这两个方法：

1. siftDown 是把指定节点与其子节点中较小的一个比较，父节点较大时“下沉（down）”；

2. siftUp 是把指定节点与其父节点比较，若小于父节点，则“上浮（up）”。

出队操作 ：poll()

public E poll() {

// 队列为空时，返回 null

if (size == 0)

return null;

int s = --size;

modCount++;

// 队列第一个元素

E result = (E) queue[0];

// 队列最后一个元素

E x = (E) queue[s];

// 把最后一个元素置空

queue[s] = null;

if (s != 0)

// 下沉

siftDown(0, x);

return result;

}

操作的示意图如下：

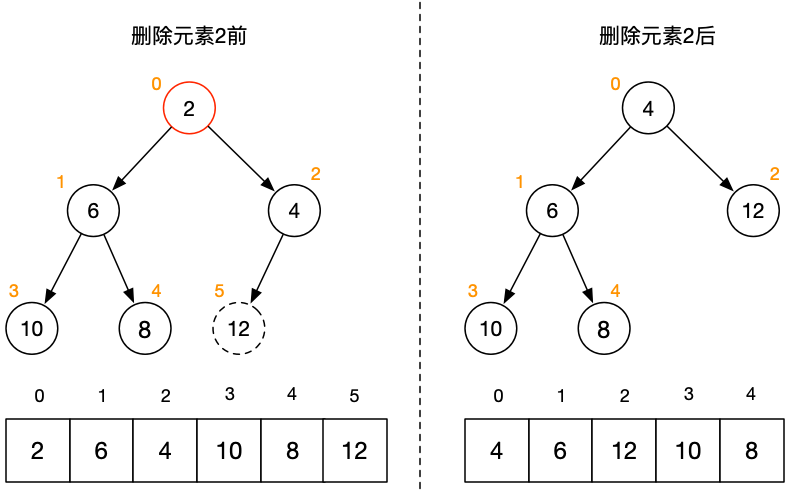
该操作的步骤大概如下：

1. 移除队列的最后一个元素，并将该元素置于首位；

2. 将新的“首位”元素与子节点中较小的一个比较，比较并交换位置（即执行“下沉（siftDown）”操作）。

删除操作 ：remove(Object)

public boolean remove(Object o) {

int i = indexOf(o);

if (i == -1)

return false;

else {

removeAt(i);

return true;

}

}

indexOf(o):

// 遍历数组查找指定元素

private int indexOf(Object o) {

if (o != null) {

for (int i = 0; i < size; i++)

if (o.equals(queue[i]))

return i;

}

return -1;

}

removeAt(i):

private E removeAt(int i) {

// assert i >= 0 && i < size;

modCount++;

int s = --size;

// 移除末尾元素，直接置空

if (s == i) // removed last element

queue[i] = null;

else {

// 末尾元素

E moved = (E) queue[s];

queue[s] = null; // 删除末尾元素

// 操作与 poll 方法类似

siftDown(i, moved);

// 这里表示该节点未进行“下沉”调整，则执行“上浮“操作

if (queue[i] == moved) {

siftUp(i, moved);

if (queue[i] != moved)

return moved;

}

}

return null;

}

大概执行步骤：

1. 若移除末尾元素，直接删除；

2. 若非末尾元素，则将末尾元素删除，并用末尾元素替换待删除的元素；

3. 堆化操作：先执行“下沉（siftDown）”操作，若该元素未“下沉”，则再执行“上浮（siftUp）”操作，使得数组删除元素后仍满足堆结构。

示例代码

示例一：

private static void test1() {

// 不指定比较器（默认从小到大排序）

Queue<Integer> queue = new PriorityQueue<>();

for (int i = 0; i < 10; i++) {

queue.add(random.nextInt(100));

}

while (!queue.isEmpty()) {

System.out.print(queue.poll() + ". ");

}

}

/* 输出结果（仅供参考）：

* 2, 13, 14, 36, 39, 40, 43, 55, 83, 88,

*/

示例二：指定比较器（Comparator）

private static void test2() {

// 指定比较器（从大到小排序）

Queue<Integer> queue = new PriorityQueue<>(11, (o1, o2) -> o2 - o1);

for (int i = 0; i < 10; i++) {

queue.add(random.nextInt(100));

}

while (!queue.isEmpty()) {

System.out.print(queue.poll() + ", ");

}

}

/* 输出结果（仅供参考）：

* 76, 74, 71, 69, 52, 49, 41, 41, 35, 1,

*/

示例三：求 Top N

public class FixedPriorityQueue {

private PriorityQueue<Integer> queue;

private int maxSize;

public FixedPriorityQueue(int maxSize) {

this.maxSize = maxSize;

// 初始化优先队列及比较器

// 这里是从大到小（可调整）

this.queue = new PriorityQueue<>(maxSize, (o2, o1) -> o2.compareTo(o1));

}

public void add(Integer i) {

// 队列未满时，直接插入

if (queue.size() < maxSize) {

queue.add(i);

} else {

// 队列已满，将待插入元素与最小值比较

Integer peek = queue.peek();

if (i.compareTo(peek) > 0) {

// 大于最小值，将最小值移除，该元素插入

queue.poll();

queue.add(i);

}

}

}

public static void main(String[] args) {

FixedPriorityQueue fixedQueue = new FixedPriorityQueue(10);

for (int i = 1; i <= 100; i++) {

fixedQueue.add(i);

}

Iterable<Integer> iterable = () -> fixedQueue.queue.iterator();

System.out.println("队列中的元素：");

for (Integer integer : iterable) {

System.out.print(integer + ", ");

}

System.out.println();

System.out.println("最大的 10 个：");

while (!fixedQueue.queue.isEmpty()) {

System.out.print(fixedQueue.queue.poll() + ", ");

}

}

}

/* 输出结果：

* 队列中的元素：

* 91, 92, 94, 93, 96, 95, 99, 97, 98, 100,

* 最大的 10 个：

* 91, 92, 93, 94, 95, 96, 97, 98, 99, 100,

*/

小结

1. PriorityQueue 为优先队列，实现了 Queue 接口，但并非阻塞对列；

2. 内部的元素是可比较的（Comparable 或 Comparator），元素不能为空；

3. 逻辑上使用「堆」（即完全二叉树）结构实现，物理上基于「动态数组」存储；

4. PriorityQueue 可用作求解 Top N 问题。

参考链接：

https://blog.csdn.net/qq_35326718/article/details/72866180

https://my.oschina.net/leejun2005/blog/135085

Stay hungry, stay foolish.